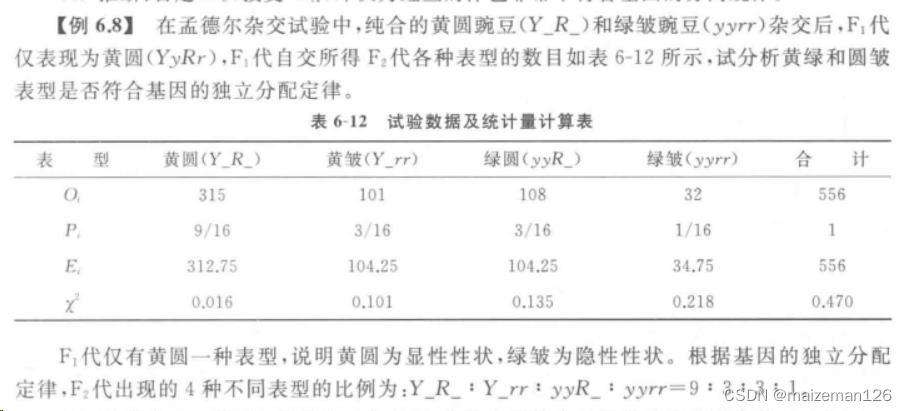
参考资料：生物统计学

       适合性检验是卡方检验应用的一种类型，检验实际的观测数与通过某一理论模型计算所得理论数是否相符，相当于1×c列联表的卡方检验，也成为单因素离散型数据的卡方检验。

       对参数的建设检验总是假定对照总体的分布数据某个确定的类型（如正态分布），从而对研究总体的未知参数（如平均数、方差）进行假设检验。因此，知道一个总体的概率分布十分重要。优势可以根据对事物本质的分析，利用概率论的知识给予回答。但在多数情况下，只能从样本数据中发现规律，判断总体的分布，这就是所谓的拟合问题。

1、正态分布的适合性检验

        在对连续性变量进行卡方适合性检验时，首先要将全部观测值划分为k类，整顿成频数表，然后根据正态分布计算各组的理论值，最后比较观测数与理论数之间的差异。若差异显著，说明观测数不符合该理论分布；反之，则认为符合该理论分布。

理论数的计算步骤如下：

（1）编制频数分数表：卡方检验要求各组理论数不小于5，不满足要求时需对相邻的组进行合并。

（2）计算各组的理论数：对各组的上下限进行标准化处理，计算各组段的正态分布概率，然后根据概率和观测总次数计算理论数。

       其中，自由度df=k-1-r，k为数据分组数，r为利用样本估计的总体参数的个数。当总体参数μ和σ均已知时，r=0；当总体参数μ和σ均未知时，r=2。

卡方统计量的计算仍为：

excel操作步骤如下：

2、二项分布的适合性检验

      遗传学上，经常需要回答某一遗传性状是否受一对等位基因的控制，该基因在后代的分离比例是否符合自由组合规律等问题。一些遗传学试验的结果为两种互斥的情况之一，例如孟德尔试验中豌豆子叶的颜色为黄色或绿色，而根据遗传学的规律，出现不同类型的概率是确定的。这些否符合二项分布的特点。

       二项分布适合性检验的理论数通过理论分布的比例进行计算。由于分布的比例是确定的，不存在参数的估计，所以自由度df=k-1。需要注意，当自由度df=1时，计算统计量时需要进行连续矫正。

引用书中案例如下：