文章目录
- 一、647、回文子串
- 二、516、最长回文子序列
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、647、回文子串

思路分析:判断一个字符串是否为回文串那么必须确定回文串的所在区间,而一维数组无法描述区间,因此我们需要用一个二维的dp数组来表示。我们只需要统计dp数组中回文串的个数即可。
- 第一步,动态数组的含义。 d p [ i ] [ j ] dp[i][j] dp[i][j]代表区间 [ i , j ] [i, j] [i,j](左闭右闭)的字符串是否为回文串。dp数组的类型为bool类型。
- 第二步,递推公式。 d p [ i ] [ j ] dp[i][j] dp[i][j]可以由两种情况推导出来:
- s [ i ] s[i] s[i] s [ j ] s[j] s[j]相等:若 i = j i = j i=j,仅一个字符(例如a),那么必然是回文串;若 j − i = 1 j - i = 1 j−i=1,两个字符(例如aa),那么也是回文串;剩下的情况: [ i , j ] [i, j] [i,j]的字符串是否为回文串与 [ i + 1 , j − 1 ] [i + 1, j - 1] [i+1,j−1]的字符串是否为回文串相同,即 d p [ i ] [ j ] = d p [ i + 1 ] [ j − 1 ] dp[i][j] = dp[i + 1][j - 1] dp[i][j]=dp[i+1][j−1]。
- s [ i ] s[i] s[i] s [ j ] s[j] s[j]不相等:那么 d p [ i ] [ j ] = f a l s e dp[i][j] = false dp[i][j]=false。
if (s[i] == s[j]) {if (j - i <= 1 || dp[i + 1][j - 1]) {result++;dp[i][j] = true;}}else dp[i][j] = false;
- 第三步,元素初始化。所有元素全部假设为false。
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
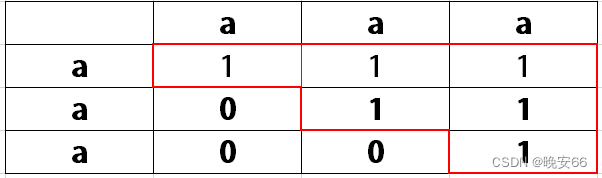
- 第四步,递归顺序。从递归公式 d p [ i ] [ j ] = d p [ i + 1 ] [ j − 1 ] dp[i][j] = dp[i + 1][j - 1] dp[i][j]=dp[i+1][j−1]中可以看出, d p [ i ] [ j ] dp[i][j] dp[i][j]需要反对角线上的元素。因此我们需要先让最下面一行的元素先有结果。同时,按定义来说 d p [ i ] [ j ] dp[i][j] dp[i][j]是一个对称句矩阵,循环只要覆盖主对角线及其上方的元素即可(如图所示)。
- 第五步,打印结果。
程序如下:
// 647、回文子串-动态规划
class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) { // 从下往上行遍历for (int j = i; j < s.size(); j++) { // 从前往后列遍历if ((s[i] == s[j]) && (j - i <= 1 || dp[i + 1][j - 1])) {result++;dp[i][j] = true;}}}return result;}
};
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2)。
二、516、最长回文子序列

思路分析:本题的分析思路和647题差不多。
- 第一步,动态数组的含义。 d p [ i ] [ j ] dp[i][j] dp[i][j]代表区间 [ i , j ] [i, j] [i,j](左闭右闭)的字符串的最大回文串长度。
- 第二步,递推公式。 d p [ i ] [ j ] dp[i][j] dp[i][j]可以由两种情况推导出来:
- s [ i ] s[i] s[i] s [ j ] s[j] s[j]相等:那么 d p [ i ] [ j ] = d p [ i + 1 ] [ j − 1 ] + 2 dp[i][j] = dp[i + 1][j - 1] + 2 dp[i][j]=dp[i+1][j−1]+2。
- s [ i ] s[i] s[i] s [ j ] s[j] s[j]不相等:那么说明加入 s [ i ] s[i] s[i]和 s [ j ] s[j] s[j]不能使回文串长度增加。那么单独加入 s [ i ] s[i] s[i]或 s [ j ] s[j] s[j]看看那个能组成最长的回文子序列,加入 s [ i ] s[i] s[i]的回文子序列长度为 d p [ i ] [ j − 1 ] dp[i][j-1] dp[i][j−1],加入 s [ j ] s[j] s[j]的回文子序列长度为 d p [ i + 1 ] [ j ] dp[i+1][j] dp[i+1][j],二者取大值,即 d p [ i ] [ j ] = m a x ( d p [ i ] [ j − 1 ] , d p [ i + 1 ] [ j ] ) dp[i][j] = max(dp[i][j-1], dp[i+1][j]) dp[i][j]=max(dp[i][j−1],dp[i+1][j])。
if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;}else {dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);}
- 第三步,元素初始化。 i = j i = j i=j的一个字符串就是回文串,其他情况的dp数组元素全部初始化为0。
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
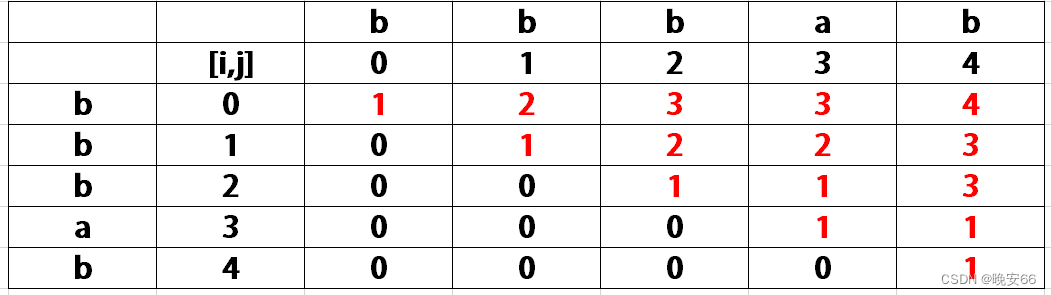
- 第四步,递归顺序。 d p [ i ] [ j ] dp[i][j] dp[i][j]依赖于 d p [ i + 1 ] [ j − 1 ] dp[i + 1][j - 1] dp[i+1][j−1], d p [ i + 1 ] [ j ] dp[i + 1][j] dp[i+1][j]和 d p [ i ] [ j − 1 ] dp[i][j - 1] dp[i][j−1]。那么递归顺序需要从下往上,从前往后递归。
- 第五步,打印结果。
程序如下:
// 516、最长回文子序列-动态规划
class Solution2 {
public:int longestPalindromeSubseq(string s) {vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;for (int i = s.size() - 1; i >= 0; i--) { // 从下往上行遍历for (int j = i + 1; j < s.size(); j++) { // 从前往后列遍历if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2;else dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);}}return dp[0][s.size() - 1];}
};
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2)。
三、完整代码
# include <iostream>
# include <vector>
# include <string>
using namespace std;// 647、回文子串-动态规划
class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) { // 从下往上行遍历for (int j = i; j < s.size(); j++) { // 从前往后列遍历if ((s[i] == s[j]) && (j - i <= 1 || dp[i + 1][j - 1])) {result++;dp[i][j] = true;}}}return result;}
};// 516、最长回文子序列-动态规划
class Solution2 {
public:int longestPalindromeSubseq(string s) {vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;for (int i = s.size() - 1; i >= 0; i--) { // 从下往上行遍历for (int j = i + 1; j < s.size(); j++) { // 从前往后列遍历if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2;else dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);}}return dp[0][s.size() - 1];}
};int main() {//string s = "aaa"; // 测试案例//Solution s1;//int result = s1.countSubstrings(s);string s = "bbbab";Solution2 s1;int result = s1.longestPalindromeSubseq(s);cout << result << endl;system("pause");return 0;
}
end