文章目录
- 一.树状数组概览
- 二.树状数组构造定义
- lowbit运算
- 树状数组的结点值的定义
- 树状数组结点层次的定义
- 树状数组父子结点关系定义
- 三.关于树状数组结构的重要证明
- 引理1
- 引理2
- 树状数组模板题
一.树状数组概览
- 树状数组的下标从
1开始标识,其物理结构是线性表,逻辑结构是一颗多叉树
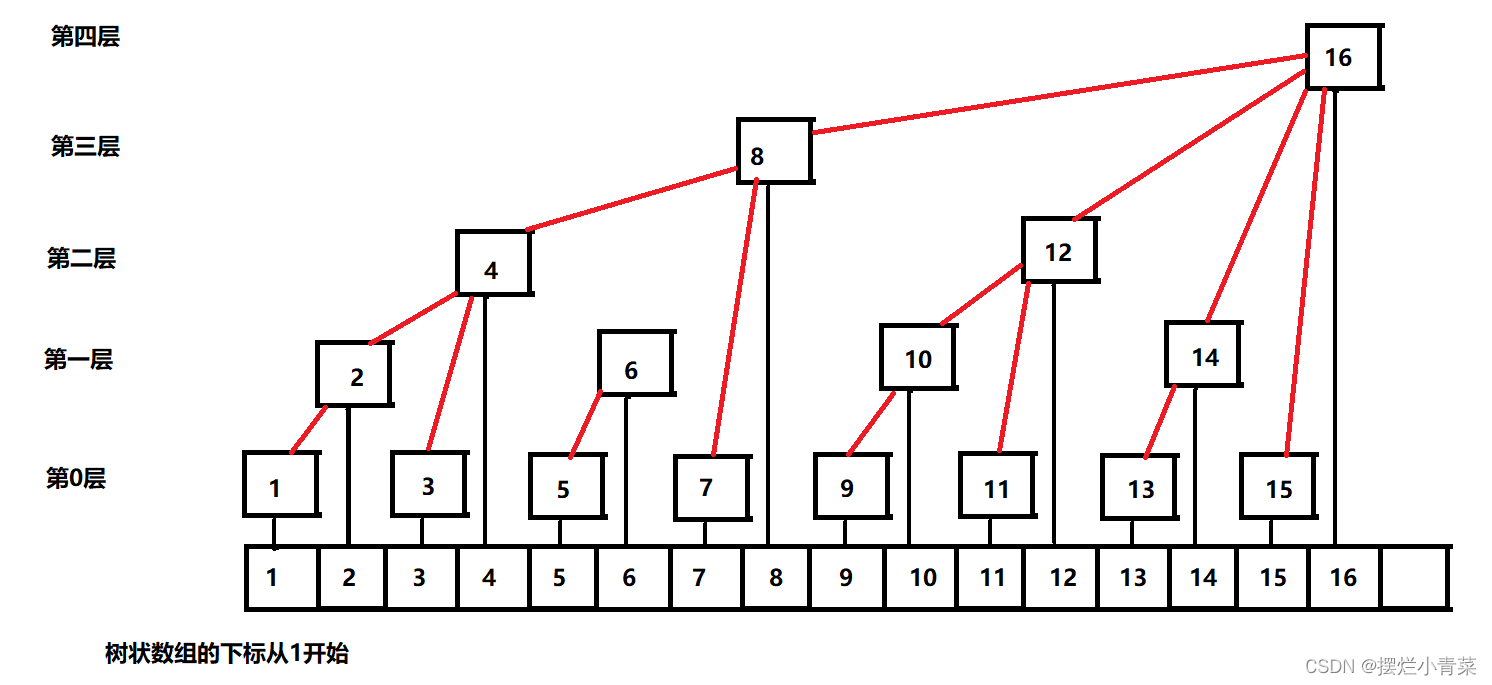
- 对于一个原数组,树状数组可以动态维护原数组的区间和
- 下文中
[]表示闭区间(包含端点),()表示开区间(不包含端点)
二.树状数组构造定义
lowbit运算
- 得到一个整数二进制最低位的
1的运算
int lowbit(int n){return n & (-n);
}
- 根据计算机补码原理不难证明:
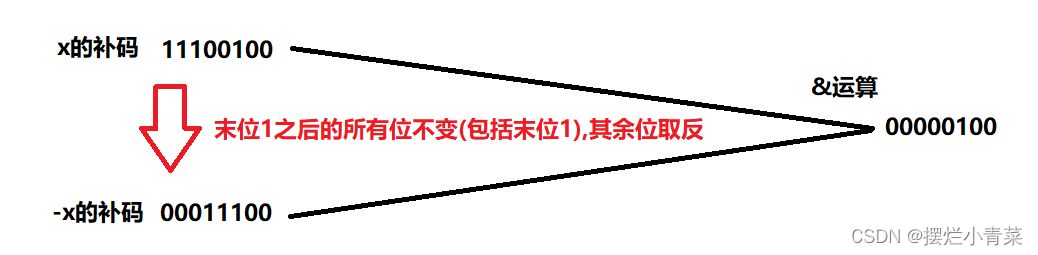
树状数组的结点值的定义
-
设原数组为
arr,树状数组为Tree,Tree[n]表示原数组arr下标区间[n-lowbit(n)+1,n]中所有数的和
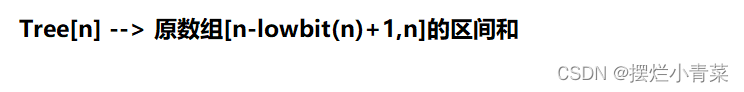
-
根据树状数组的结点值的定义,很容易可以得到一个求原数组前缀和的递归表达式:

-
现有树状数组
Tree,可以给出求原数组arr区间[1,n]前缀和的函数:
int Get_Sum(int * Tree,int n){if(n == 0)return 0;return Get_Sum(Tree,n - lowbit(n)) + Tree[n];
}
- 不难分析,该递归函数的时间复杂度为
logN级别
树状数组结点层次的定义
- 树状数组
Tree[n]结点的层次为n二进制表示末位连续0的个数 - 根据该定义可知,树状数组所有奇数位结点层次全部为0
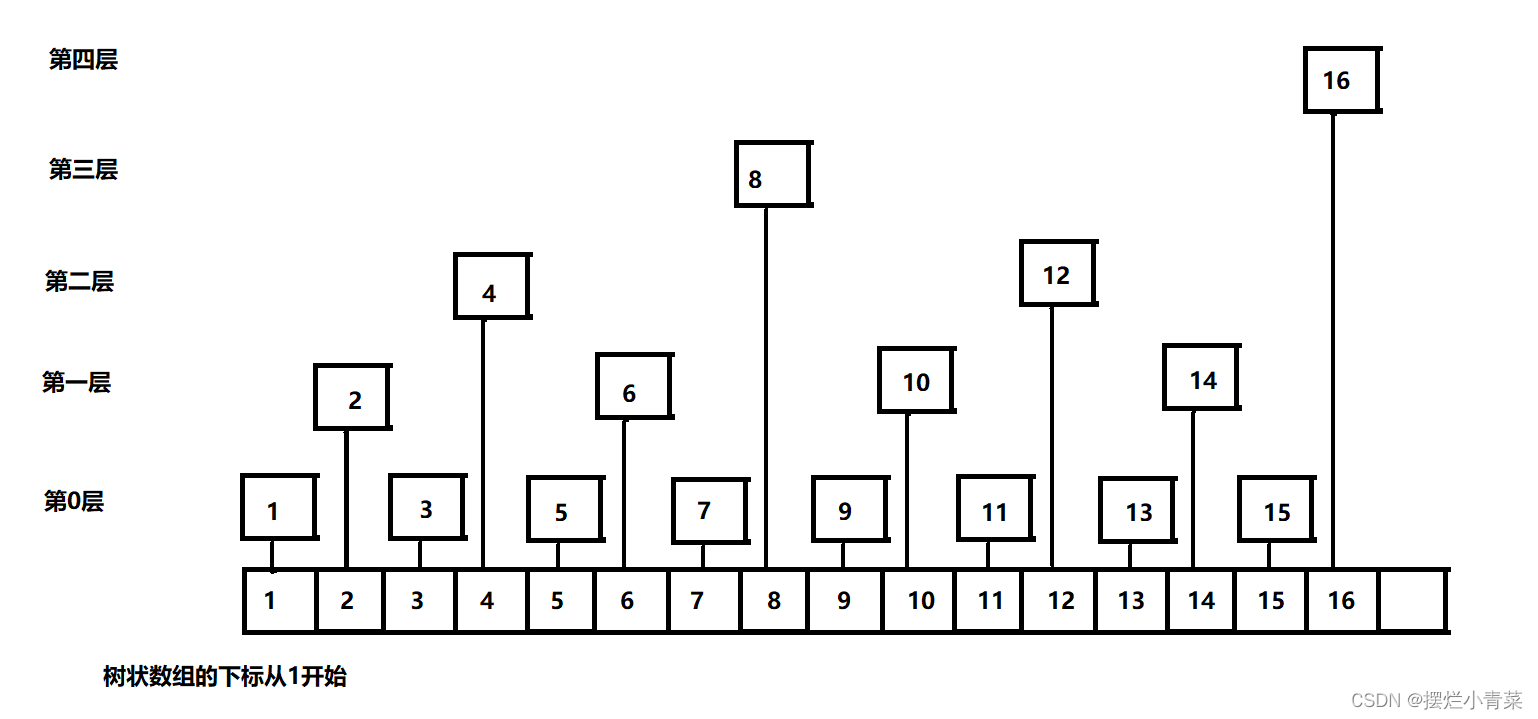
- 根据该定义可知,设树状数组中结点
x的层数为k,则结点x+lowbit(x)的层数一定大于k(根据lowbit运算的定义很容易可以证明)
树状数组父子结点关系定义
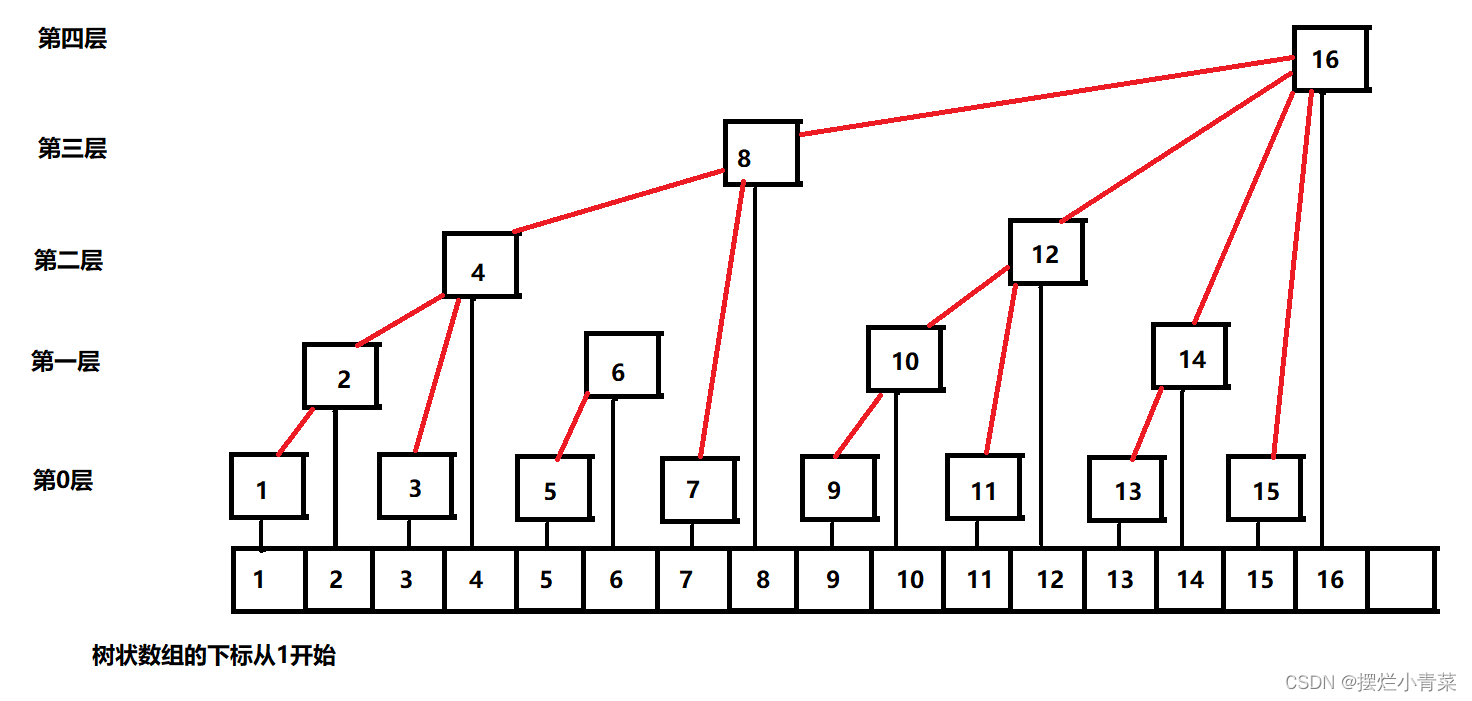
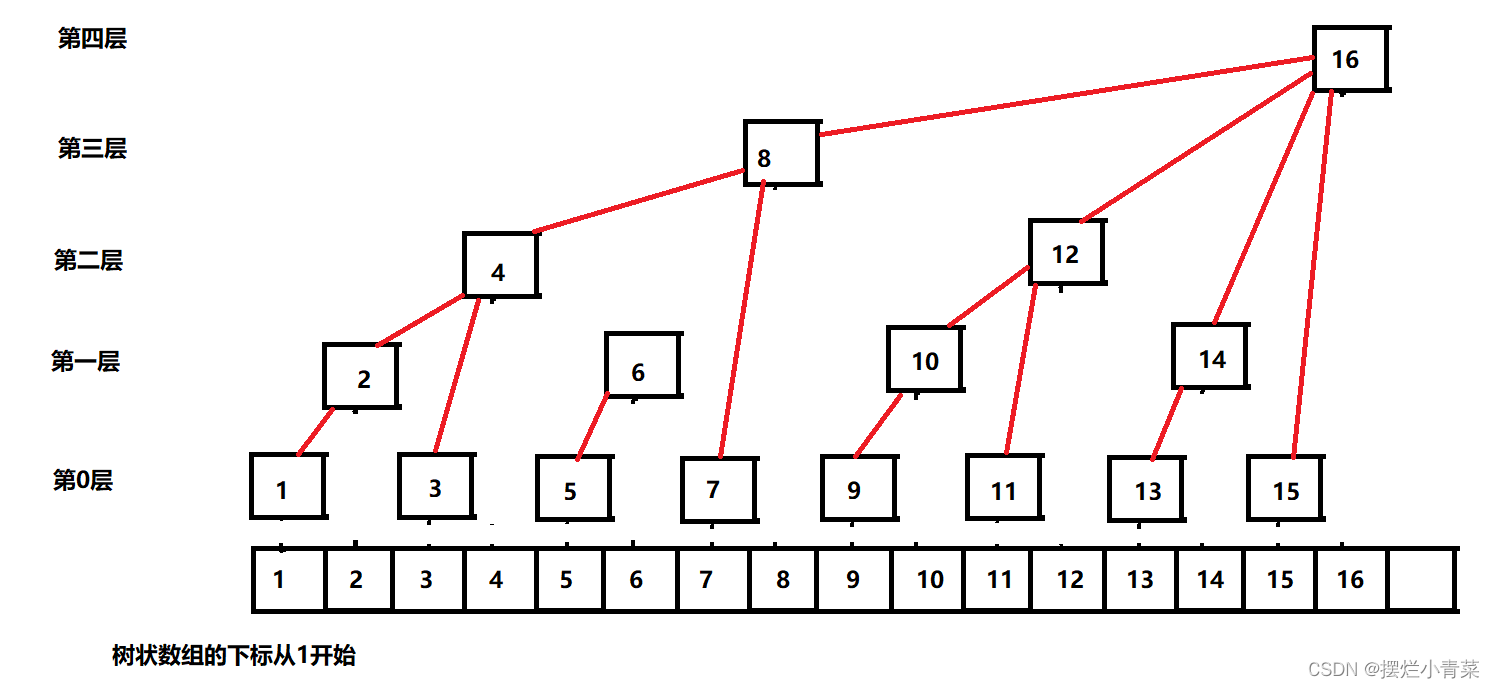
- 树状数组
Tree[n]结点的父节点定义为:Tree[n+lowbit(n)] - 根据上述定义,可以直观地感受一下树状数组的逻辑结构:
三.关于树状数组结构的重要证明
引理1
- 引理1:树状数组第x个结点的父结点所代表的原数组和区间
[x+lowbit(x)-lowbit(x+lowbit(x))+1,x+lowbit(x)]包含x- 由于
lowbit(x + lowbit(x)) > lowbit(x),所以x+lowbit(x)-lowbit(x+lowbit(x))+1 <= x,引理1成立
- 由于
引理2
- 引理2:树状数组第x个结点到其父结点之间的所有节点(不包括x结点和其父结点)所代表的原数组的和区间不包含x
- 证明:

- 最严格的证明应写成数学表达式,但考虑到直观性,这里略过了(其实并不难)
- 证明:
- 根据引理1和引理2,当原数组某个数arr[i]改变Δx时,树状数组只需从结点Tree[i]开始,沿着树中的路径向上层将每一个结点的值改变Δx就可以维持树状数组的数据结构完整性,实现了区间和的动态更新,时间复杂度为
logN
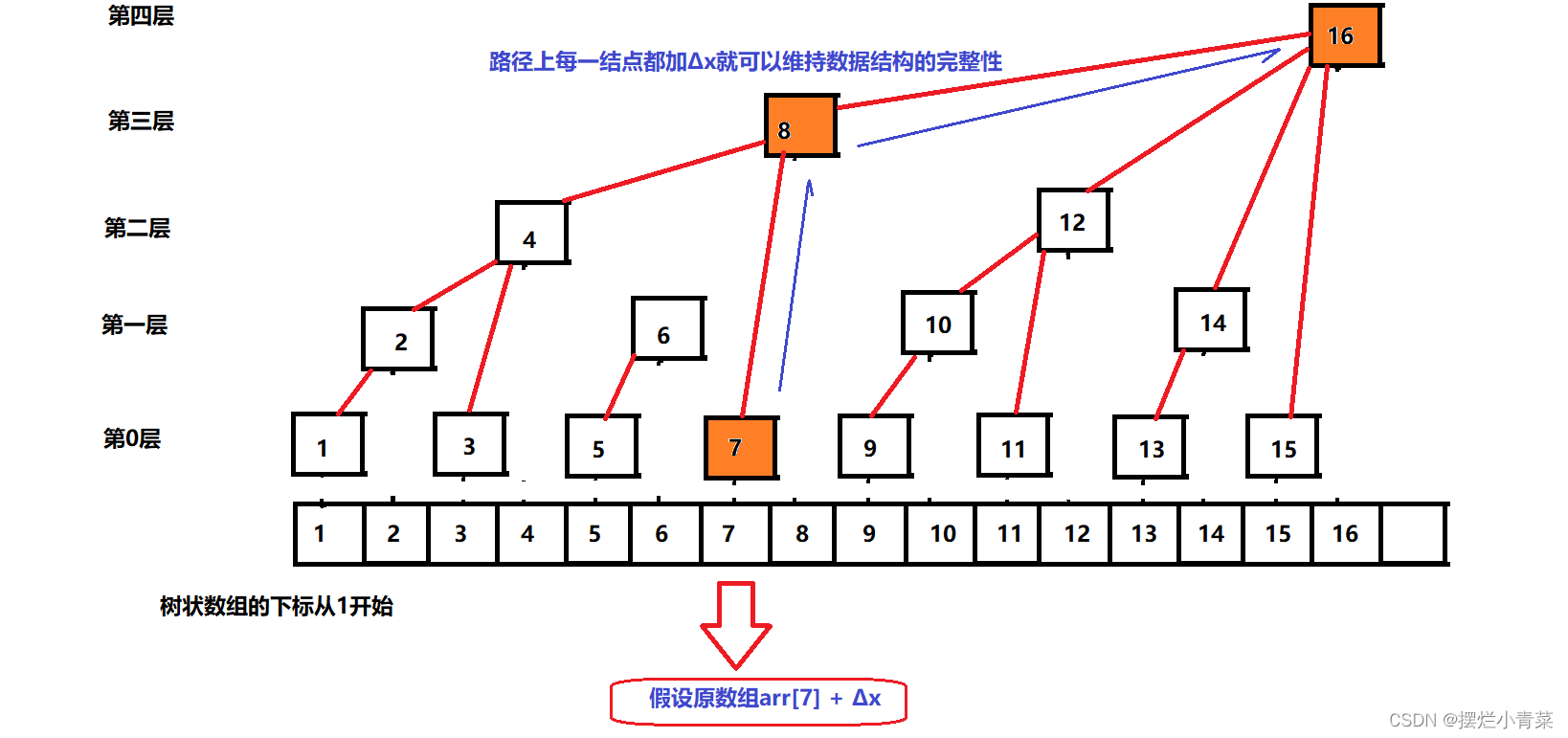
- 原数组第
n个元素改变change,树状数组Tree的更新函数:
//size表示树状数组的长度
void UpDate(int * Tree ,int size,int n , int change){for(int i = n ; i <= size ; i+=lowbit(i)){Tree[i] += change;}
}
树状数组模板题
树状数组模板题1
树状数组模板提2