挑战自己,每天进步一点点,成就将属于不停止脚步的你。
目录
Redis集合?
集合基本命令
sadd
smembers
sismember
scard
spop
srandmember
smove
srem
集合间操作
sinter
sinterstore
sunion
sdiff
sdiifstore

Redis集合?
集合就是把一些有关的数据放在一起,你可以思考一下数学中的集合,离散数学中的集合里面的元素是不区分顺序的。不同于list,list中的元素如果元素都相同,但是有两个元素的顺序不一样,那么这两个列表就不相同。
集合类型也是保存多个字符串类型的元素的,但和列表类型不同的是,集合中:
- 元素之间是无序的
- 元素不允许重复
一个集合中最多可以存储2^32 − 1 个元素。Redis 除了支持集合内的增删查改操作,同时还支持多个集合取交集、并集、差集,合理地使用好集合类型,能在实际开发中解决很多问题。
下面是一个集合的图解:
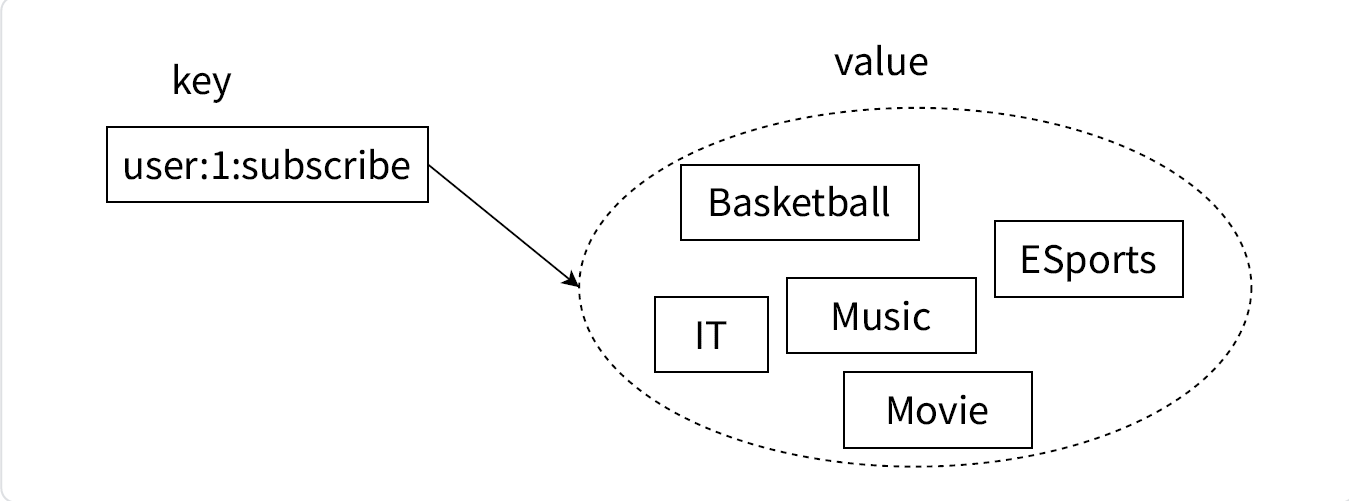
集合基本命令
集合的操作命令,都是带有S前缀的。
sadd
将一个或者多个元素添加到 set 中。注意,重复的元素无法添加到 set 中。
语法:sadd key member [ member1 member2 ... ]
- 时间复杂度:O(1)
- 返回值:本次添加成功的元素的个数。
- 一次性可以添加多个member,多个member之间使用空格间隔。
示例:

集合石要求不能重复的:

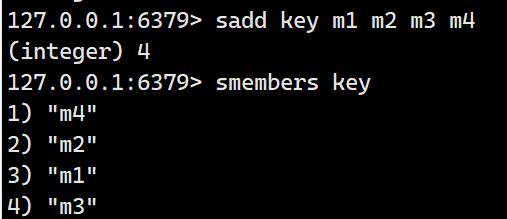
smembers
获取一个 set 中的所有元素,注意,元素间的顺序是无序的.
语法:smembers key
- 时间复杂度:O(N)
- 返回值:所有元素的列表。
示例:
sismember
判断一个元素在不在 set 中。
语法:sismember key member
- 时间复杂度:O(1)
- 返回值:1 表示元素在 set 中。0 表示元素不在 set 中或者 key 不存在。
示例:

scard
全称:set cardinality。获取一个 set 的基数(cardinality),即 set 中的元素个数。这个基数可以理解为数量的意思。
语法:scard key
- 时间复杂度:O(1)
- 返回值:set 内的元素个数。
示例:

pop一般表示列表中的删除一个元素。但是集合的元素是无序的,因此删除是随机的。
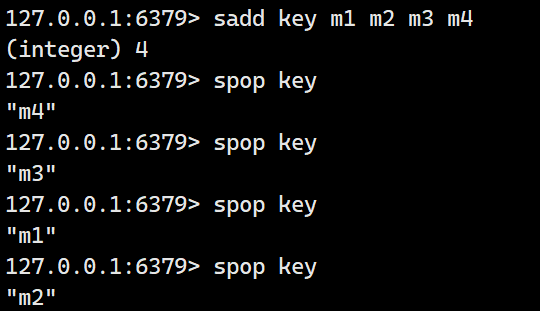
spop
从集合中随机删除一个member
语法:spop key [ count ]
- count表示删除的个数,不写的时候默认为1,删除一个,写了之后就会删除指定的count个。
- 返回值为被删除的member的值。
- 时间复杂度:O(N), n 是 count
示例:
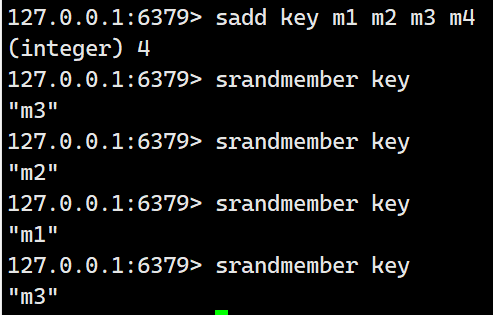
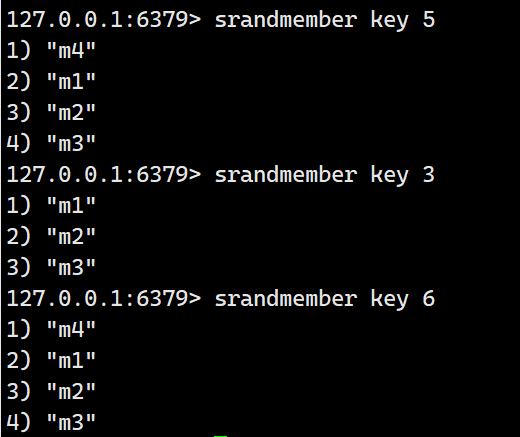
srandmember
随机从set中获取一个member,该方法并不会删除该被获取的member。
语法: srandmember key [count]
- 时间复杂度O(1)
- 返回值:随机获取的一个member的值。
- 可以指定生成的随机member的次数。
示例:
指定count:
smove
将一个元素从源 set 取出并放入目标 set 中
语法:smove sourceKey destinationKey member
- 时间复杂度:O(1)
- 返回值:1 表示移动成功,0 表示失败
示例:
创建源key:

创建destination key:

他们都共有一个m1,然后将sourceKey中的元素移动到destinationKey当中:

移动成功之后返回1:

但是由于这里的destinationKey已经有一个m1,所以不会有明显的改变。
下面移动一个其他的member:

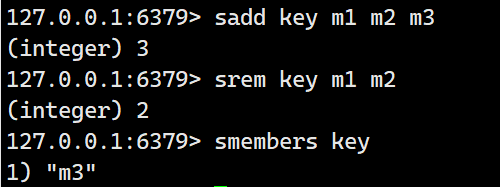
srem
将指定的元素从 set 中删除。
语法:srem key member [member ... ]
- 时间复杂度:O(N), N 是要删除的元素个数
- 返回值:本次操作删除的元素个数。
示例:
集合间操作
集合在算法设计和复杂性理论中也发挥着重要作用。集合的操作和性质为解决许多计算问题提供了基础,例如图论、优化问题和网络流问题等。集合是计算机科学中许多算法和数据结构的核心概念
集合的操作并不只针对里面的元素,集合的操作还可以对两个集合本身进行操作。两个集合之间可以进行交集(inter),并集(union),差集(diff)的计算。



sinter
获取给定 set 的交集中的元素。
语法:sinter key [key... ]
- 时间复杂度:O(N * M), N 是最小的集合元素个数. M 是最大的集合元素个数
- 返回值:交集的元素
示例:

求交集:

另外一个版本的求交集
sinterstore
获取给定 set 的交集中的元素并保存到目标 set 中
语法:sinterstore destKey key [ key ... ]
- 时间复杂度:O(N * M), N 是最小的集合元素个数. M 是最大的集合元素个数
- 返回值:交集的元素个数
- destKey为结果集的存放目标。
示例:
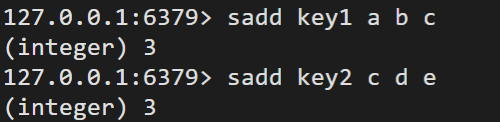
设置两个setkey
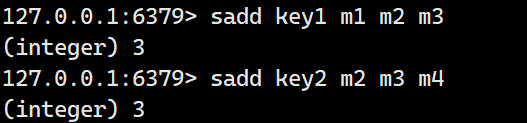
执行交集操作:

查看结果:

sunion
求多个集合中的并集。
语法:sunion key [ key ... ]
- 时间复杂度:O(N), N 给定的所有集合的总的元素个数
- 返回值:并集的元素。
示例:

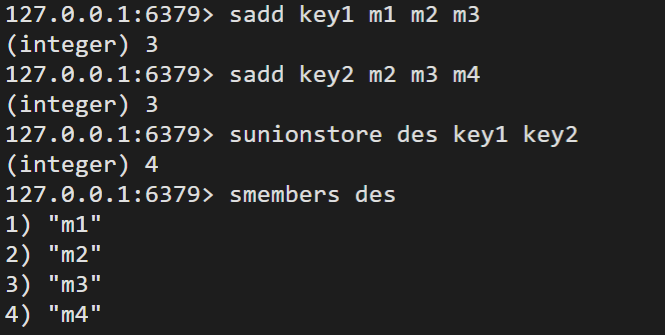
sunionstore
获取给定 set 的并集中的元素并保存到目标 set 中。
语法:sunionstore destination key [key ...]
- 时间复杂度:O(N), N 给定的所有集合的总的元素个数.
- 返回值:并集的元素个数。
示例:
sdiff
获取给定 set 的差集中的元素。
语法:SDIFF key [key ...]
- 时间复杂度:O(N), N 给定的所有集合的总的元素个数.
- 返回值:差集的元素。
示例:

反过来:

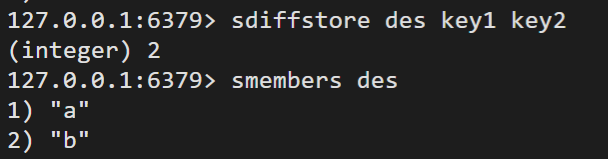
sdiifstore
获取给定 set 的差集中的元素并保存到目标 set 中。
语法:SDIFFSTORE destination key [key ...]
- 时间复杂度:O(N), N 给定的所有集合的总的元素个数.
- 返回值:差集的元素个数。
示例:
使用sdiifstore: