给定一张 n
个点的带权无向图，点从 0∼n−1
标号，求起点 0
到终点 n−1
的最短 Hamilton 路径。

Hamilton 路径的定义是从 0
到 n−1
不重不漏地经过每个点恰好一次。

输入格式
第一行输入整数 n
。

接下来 n
行每行 n
个整数，其中第 i
行第 j
个整数表示点 i
到 j
的距离（记为 a[i,j]
）。

对于任意的 x,y,z
，数据保证 a[x,x]=0，a[x,y]=a[y,x]
并且 a[x,y]+a[y,z]≥a[x,z]
。

输出格式
输出一个整数，表示最短 Hamilton 路径的长度。

数据范围
1≤n≤20

0≤a[i,j]≤107
输入样例：
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例：
18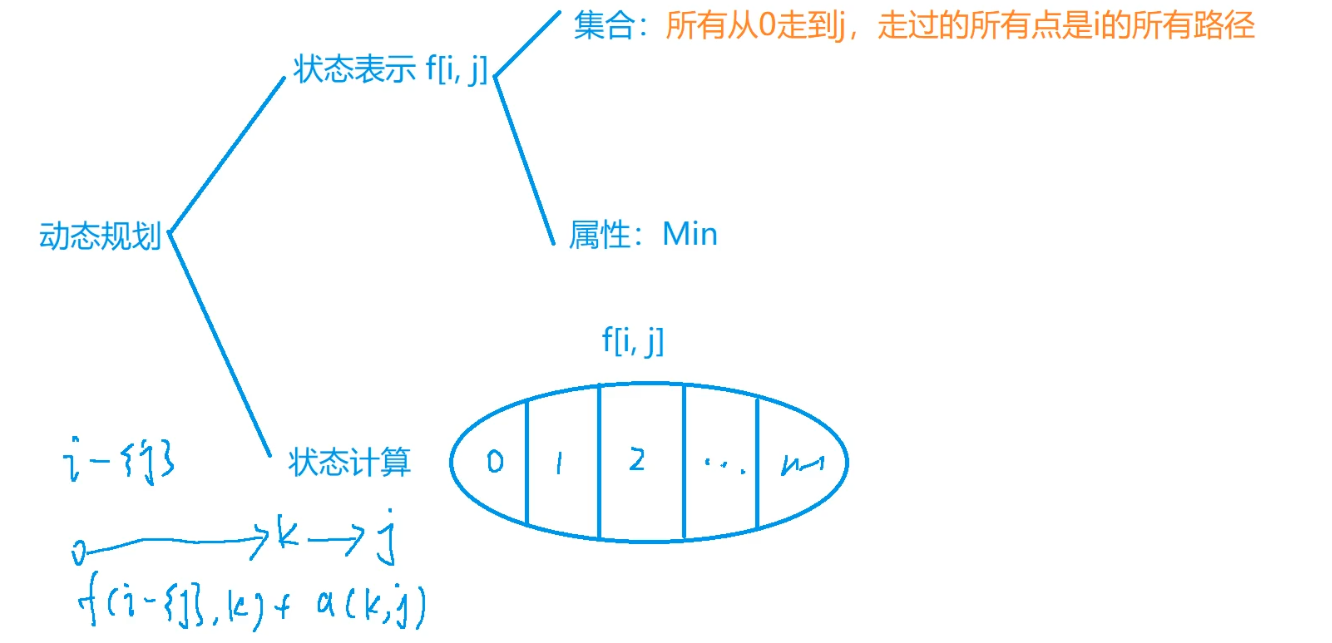

代码中的 f[i][j] 表示从起点出发，经过状态 i 中的所有顶点，最后到达顶点 j 的最短路径长度。状态 i 是一个二进制数，其中的每一位表示对应顶点是否已经经过，1 表示经过，0 表示未经过。因此，状态 i 中有多少个 1，就表示已经经过了多少个顶点。

首先，我们将 f 数组初始化为正无穷，表示初始时任意两个顶点之间的距离均为无穷大。然后，我们从起点出发，经过每一个顶点一次，最后回到起点。因此，我们从状态 1 出发，即只经过起点。这时，起点到起点的距离显然为 0，所以 f[1][0] = 0。

接下来，我们遍历所有的状态 i 和顶点 j，尝试更新 f[i][j] 的值。对于状态 i 中的每一个顶点 j，我们尝试从状态 i 中移除顶点 j，得到状态 i - (1 << j)，然后找到之前状态 i - (1 << j) 中的一个顶点 k，使得从 k 经过 j 到达终点 j 的路径最短。这样就可以更新状态 i 中顶点 j 的最短路径长度。具体来说，就是 f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j])。

最后，我们找到从任意一个顶点出发，经过所有的顶点一次后回到起点的最短路径。因此，答案就是 f[(1 << n) - 1][n - 1]，表示从状态 (1 << n) - 1（即所有顶点都经过）到达顶点 n - 1（起点）的最短路径长度。

#include <iostream>
#include <algorithm>
#include <cstring>using namespace std;const int N = 21, M = 1 << N;int n;
int w[N][N];
int f[M][N];int main ()
{scanf("%d", &n);for(int i = 0; i < n; i ++ )for(int j = 0; j < n; j ++ )scanf("%d", &w[i][j]);memset(f, 0x3f, sizeof f); // 初始化为正无穷f[1][0] = 0; // 初始化第一个点，第一维1表示只走了0号这一个点，第二维度表示从0号点（默认）走到了0号点for(int i = 0; i < 1 << n; i ++ ) for(int j = 0; j < n; j ++ )if(i >> j & 1) // 从0走到j，则i里面一定要最起码包含j才有意义，也就是判断i的第j位是否为1for(int k = 0; k < n; k ++ ) // 枚举所有转移的状态if((i - (1 << j)) >> k & 1) // 相从k这个点转移过来，则i状态除去j点后必须包含k这个点才有意义f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]); // 转移状态printf("%d\n", f[(1 << n) - 1][n - 1]);return 0;
}