基环树其实并不是树，是指有n个点n条边的图，我们知道n个点n-1条边的连通图是树，再加一条边就会形成一个环，所以基环树中一定有一个环，长下面这样：

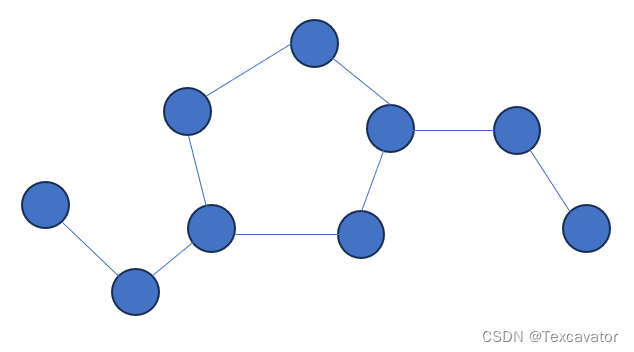
由基环树可以引申出基环内向树和基环外向树

基环内向树如下，特点是每个点的出度为1

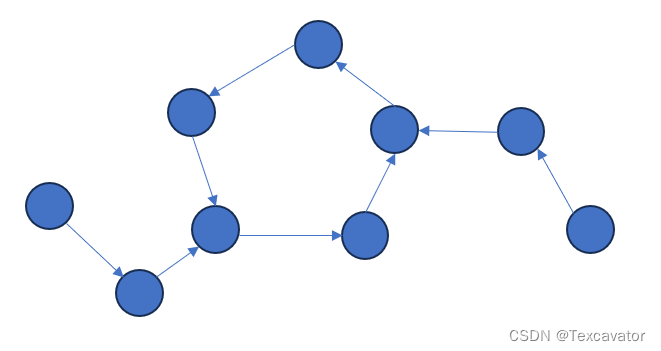
基环外向树如下，特点是每个点的入度为1

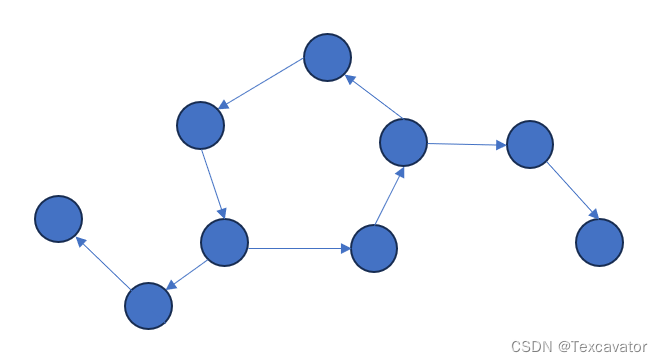
下面放点题，做到相关题目随时更新

基环树+组合数学

CF 1454E Number of Simple Paths

先记录环上的点，每个环上的点引出去的子树中，两点之间都只有一条路径，然后子树和其他点之间都有两条路径（因为有个环），可以循环计算每个子树，答案累加即可

#include <bits/stdc++.h>using namespace std;typedef pair<int, int> PII;#define int long longvoid solve()
{int n;cin >> n;vector<vector<int>> g(n + 1);vector<int> in(n + 1);for (int i = 0 ;i < n; i ++ ){int a, b;cin >> a >> b;g[a].push_back(b);g[b].push_back(a);in[a] ++ , in[b] ++ ;}queue<int> q;for (int i = 1; i <= n; i ++ ) {if (in[i] == 1) q.push(i);}while (q.size()){auto t = q.front();q.pop();for (int i = 0; i < g[t].size(); i ++ ){int j = g[t][i];in[j] -- ;if (in[j] == 1) q.push(j);}}vector<int> huan;vector<int> st(n + 1);for (int i = 1; i <= n; i ++ ){if (in[i] > 1){huan.push_back(i);st[i] = true;}}int ans = 0, sumtmp, sum = 0;vector<bool> visited(n + 1);function<void(int, int)> dfs = [&](int u, int fa){sumtmp ++ ;if (visited[u]) return;visited[u] = true;for (int i = 0; i < g[u].size(); i ++ ){int j = g[u][i];if (j == fa || visited[j] || st[j]) continue;dfs(j, u);}return;};for (auto i : huan){sumtmp = 0;dfs(i, -1);ans += sumtmp * (sumtmp - 1) / 2;ans += (sumtmp - 1) * (n - sumtmp - sum) * 2;sum += sumtmp - 1;}ans += huan.size() * (huan.size() - 1);cout << ans << '\n';
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;cin >> t;while (t -- ){solve();}
}

基环内向树+dfs

牛客 寒假集训1K 牛镇公务员考试

基环内向树（准确的说应该是森林）

编号 i 向 a[i] 连边，表示对其限制，我们可以发现环之外的链对答案没什么影响，因为确定了环上一点，可以倒推出链上的所有答案（原因就是约束关系），所以我们在环上任取一点，枚举这个点的五种答案，然后遍历一下环看这个答案是否合法

因为不保证联通，所以需要遍历每一个点

#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;const int N = 1000010;
const int maxn = 1e6 + 1;
const int mod = 998244353;void solve()
{int n;cin >> n;vector<int> a(n + 1);vector<string> s(n + 1);for (int i = 1; i <= n; i ++ ) cin >> a[i] >> s[i];vector<bool> st(n + 1);int ans = 1;for (int i = 1; i <= n; i ++ ){if (st[i]) continue;int j = i;vector<int> huan;for (; !st[j]; j = a[j]){huan.push_back(j);st[j] = true;}auto iter = find(huan.begin(), huan.end(), j);if (iter == huan.end()) continue;huan = {iter, huan.end()};int tmp = 0;for (int k = 0; k < 5; k ++ ){int h = k;for (auto t : huan) h = (int)(s[t][h] - 'A');tmp += h == k;}ans = ans * tmp % mod;}cout << ans << '\n';
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t -- ){solve();}
}