贪心算法篇

“靠漫步，将生趣填饱~”

贪心算法简介？

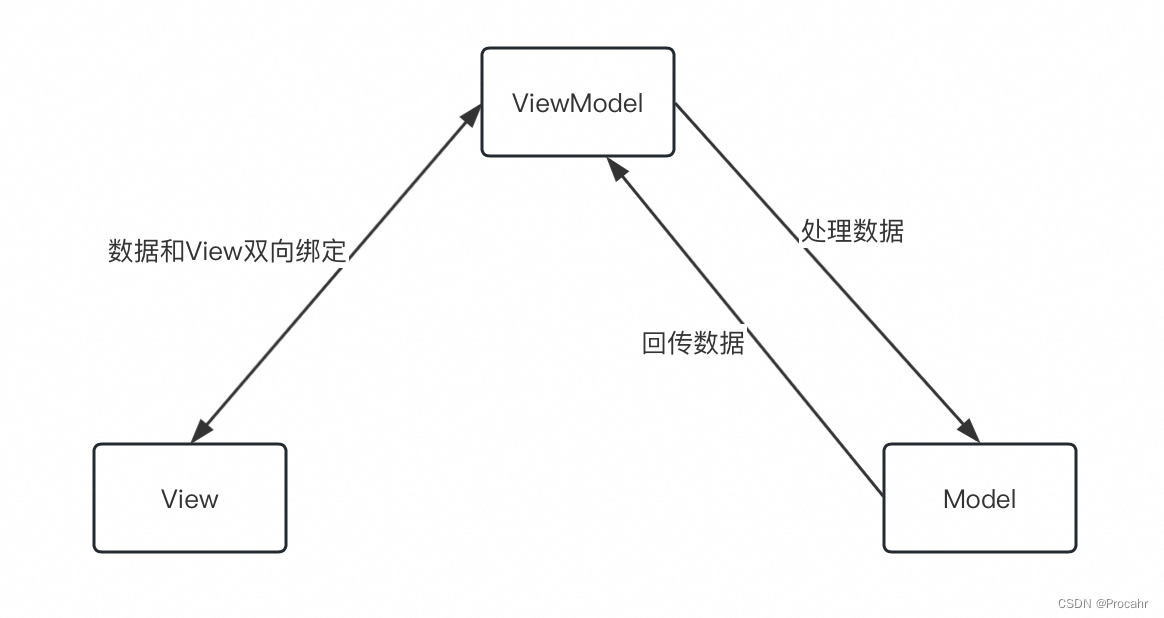
贪心算法（Greedy Algorithm），也称为贪婪算法，是一种在解决问题时采取贪心策略的方法。其基本原理是很简单的：

“在每个决策点上都选择当下看似最好的选项，而不是寻求全局最优点”。

我们举几个，常使用贪心算法的小例：

找零问题：

此时你的顾客一手掏出50“大米”递给你，一手拿着一瓶快乐水——“nutrition happy line”(you know，这瓶饮料的价格为4)。现如今，这位顾客正一脸疑惑地盯着你的一举一动，因为你接过纸币后，目不转睛地瞅着那数字不小的“大米”愣神。你总会在感到一股苍劲的凉风过后，两眼冒星，腥咸的液体会被你从口中送入食管——你应当马上给他找零了。拉开你正下方，散发着浓烈朽木味儿的抽屉，你从中看到了无数的纸币，其中的面额如下：[20, 10 , 5 ,1]。你需要使用最少的纸币，完成找零工作：

已知，我们要给这位虎背熊腰的壮汉的找零数是：46。又要求我们使用最小的纸币数，所以，我们将两张黄旧的、纸面油印为20的纸币重叠好，再选取面额分别为5和1的纸币，一并夹在手指之间，塞给了这位壮汉。我们的选择为：20 * 2 + 5 * 1 + 1 * 1 = 46。总共需要四张纸币，完成这份找零工作。这便是最少使用纸币的解法。

最小路径和:

这天你命犯桃花，因为本应对你爱答不理、而你却日夜心念的邻家小妹邀请你同她加入到这一场由神秘人创办的乐园探险中。你本以为这仅仅只是一场普通的游乐主题，彼时暗自窃喜，怀揣着想入非非的心思，幻想着邻家小妹把你相拥、同你腻歪的恋爱场景。然而，这场游戏完完全全没有表面看起来那么简单，处处透露着诡异、怪诞，你莫名被卷入到了一场恐怖的布局和惊天的阴谋之中，感受来自黑暗的惊悚：消失的人脸、怪异的乞丐、脱落的车轨以及血腥、压抑的迷宫……

每个格子的数字，代表着探寻这个九宫格格子的时间。你需要花最少的时间，进入到右下角的最后一个格子之中，从恶魔的祭奠仪式拯救邻家小妹……

上述的两个例子，对于第一个例子而言，选择的方案：“尽可能选择较大面额的纸币” ，最终我们可以得到“最优解”。相反，对于第二个例子而言，我们的选择是 “选择花费时间较少的格子”进行探索，然而事实上，得出的并不是最优解。

贪心算法通常会逐步构建问题的解空间，每次尝试将下一个待选元素加入到解集中，直到无法再添加为止。这个过程会使得问题简化为一系列子问题，每个子问题都可以通过同样的贪婪策略来解决，从而逐步接近整体的最优解。

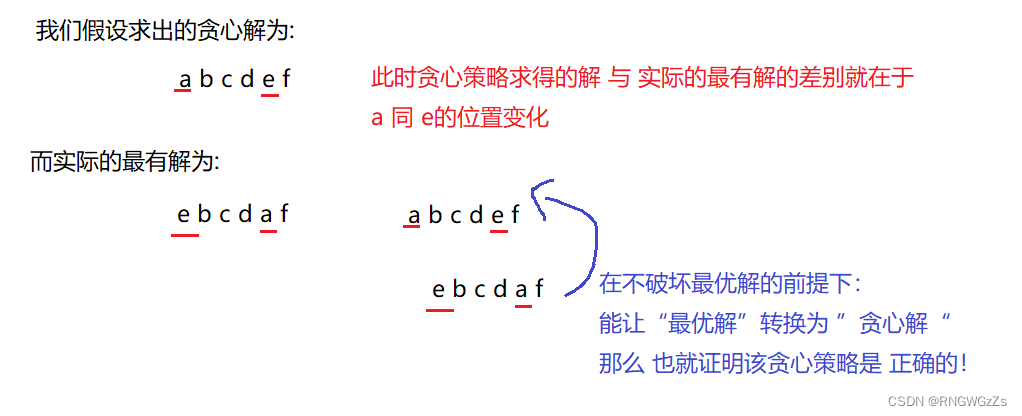
所谓的这些从局部的角度考虑选择的方案，实质上就是“贪心”策略。然而，“贪心”策略也可能是“错误”的方法，让我们得不出最有解。所以，正确的“贪心”策略，是需要进行验证、证明的。

柠檬水找零

(1) 题目解析

(2) 算法原理

class Solution {
public:bool lemonadeChange(vector<int>& bills) {// 记录5$ 10$的个数int five = 0,ten = 0;for(auto& bill:bills){if(bill == 5) five++; // 5$ 直接收下else if(bill == 10){if(five == 0) return false;  // 没有5$ 不能找零else five--;ten++;  // 收下10$}else{if(five && ten) five--,ten--; // 贪心策略:尽量保留5$else if(five > 2) five -= 3;else return false;}}return true;}
};

贪心证明:

贪心只是一种策略，考虑的角度也仅仅是局部的“最优解”，所以，贪心策略也可能是“错误的”

如何确定贪心求得的解就是最优解，还需要进行证明求真。

🥃 证明策略1：交换论证

将数组和减半的最少操作次数

(1) 题目解析

(2) 算法原理

class Solution {
public:int halveArray(vector<int>& nums) {priority_queue<double> pq;double sum = 0;for(auto n:nums){pq.push(n);sum += n;  }sum /= 2.0;// 数组减半int count = 0; // 记录操作次数while(sum > 0){double top = pq.top();pq.pop();top /= 2.0;sum -= top;pq.push(top);count++;}return count;}   
};

贪心证明:

🍷 交换论证法:

最大数

(1) 题目解析

(2) 算法原理

class Solution {
public:string largestNumber(vector<int>& nums) {vector<string> strs;for(auto x:nums) strs.push_back(to_string(x));sort(strs.begin(),strs.end(),[](const string& s1,const string& s2){return s1 + s2 > s2 + s1;});// 提取结果string res;for(auto& s:strs) res += s;// 处理前置0if(res[0] == '0') return "0";return res;}
};

贪心证明:

似乎，没有看到本题的贪心策略呢？贪心在何处？

摆动序列

(1) 题目解析

(2) 算法原理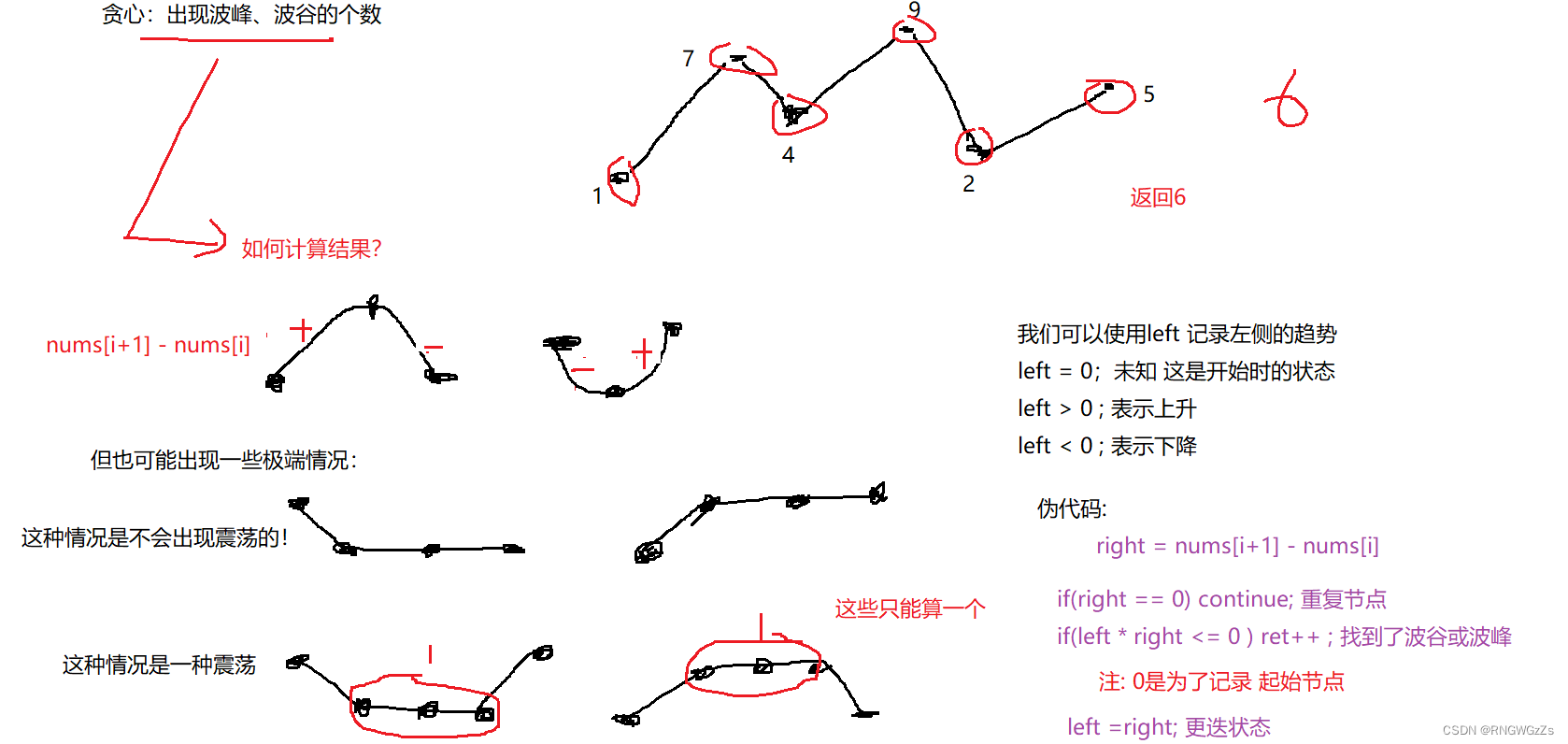

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if(nums.size() < 2) return nums.size();int ret = 0,left = 0;for(int i=0;i < nums.size() - 1;++i){int right = nums[i+1] - nums[i];if(right == 0) continue;if(left * right <=0) ret++;left = right;}// +1表示末尾节点return ret + 1;}
};