机器学习基本概念
文章目录
- 机器学习基本概念
- 1 概述
- 2 机器学习实验方法与原则
- 2.1 平均指标
- 2.2 训练集、验证集与测试集
- 2.3 随机重复实验
- 2.4 K折交叉验证
- 2.4 统计有效性检验
1 概述
-
什么是机器学习 —— 在某种任务上基于经验不断进步
T (Task):需要解决什么任务
P(Performance):任务确定什么指标
E(Experience):通过什么经验学习进步
-
归纳学习假设
任一假设若在足够大的训练样例集中很好地逼近目标函数, 它也能在未见实例中很好地逼近目标函数
-
通用机器学习系统设计
-
用于训练的经验——数据、训练过程、特征(训练数据偏差)
-
到底应该学什么——目标函数:正确 vs 可行(假设)
-
应该如何表示——函数类型必须依据表达能力仔细选取
-
具体用什么算法去学习——最小均方误差、梯度下降法
-
综合设计——数据→特征表示→算法→评价

-
-
基本概念
-
实例空间(Instance Space) X:例:每一天由一些属性描述 天空,空气温度,湿度,风,水,预报
-
假设空间(Hypothesis Space) H:例:一个假设 if (温度 = 寒冷 AND 湿度 = 高) then 打网球 = 否
-
训练样例空间(Sample Space) D:正例和负例 (基于问题设定)<x1,c(x1)> ,……, <xm,c(xm)>
-
目标概念(Target Concept) C:假设 h ∈ H h∈H h∈H,求 $ h(x)=c(x)for;all;x∈X $
全部x的实例空间太大,换成$ h(x)=c(x)for;all;x∈D $
-
-
有监督和无监督学习
有监督 无监督 训练样例 (X,Y)对,通常包含人为的努力 仅 X ,通常不涉及人力 学习目标 学习 X 和 Y 的关系 学习 X 的结构 效果衡量 损失函数 无 应用 预测: X=输入, Y=输出 分析: X=输入
2 机器学习实验方法与原则
2.1 平均指标
-
回归任务:预测值 p i p_i pi 常为连续值,需要衡量与真实值 y i y_i yi 之间的误差
-
平均绝对误差(MAE)
M A E = 1 n ∑ i = 1 n ∣ y i − p i ∣ MAE=\frac {1} {n}\sum_{i=1}^{n} {|y_i-p_i|} MAE=n1i=1∑n∣yi−pi∣ -
均方误差(MSE):预测误差较大的样本影响更大
M S E = 1 n ∑ i = 1 n ( y i − p i ) 2 MSE=\frac {1} {n}\sum_{i=1}^{n} {(y_i-p_i)^2} MSE=n1i=1∑n(yi−pi)2 -
均方根误差(RMSE):与预测值、标签单位相同
R M S E = M S E = 1 n ∑ i = 1 n ( y i − p i ) 2 RMSE=\sqrt{MSE}=\sqrt{\frac {1} {n}\sum_{i=1}^{n} {(y_i-p_i)^2}} RMSE=MSE=n1i=1∑n(yi−pi)2
-
-
分类任务:预测值一般为离散的类别,需要判断是否等于真实类别
-
准确率(Accuracy)
A c c u r a c y = 1 n ∑ i = 1 n ( y i = p i ) Accuracy=\frac {1} {n}\sum_{i=1}^{n} {(y_i=p_i)} Accuracy=n1i=1∑n(yi=pi) -
错误率(Error Rate)
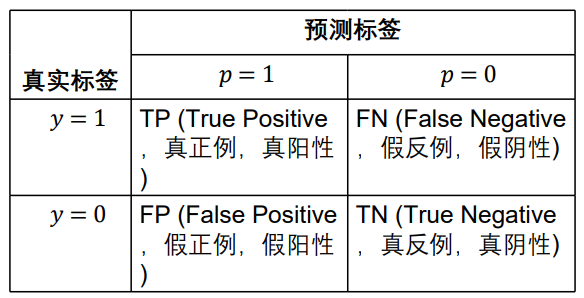
E r r o r R a t e = 1 − A c c u r a c y = 1 − 1 n ∑ i = 1 n ( y i = p i ) Error\,Rate = 1-Accuracy=1-\frac {1} {n}\sum_{i=1}^{n} {(y_i=p_i)} ErrorRate=1−Accuracy=1−n1i=1∑n(yi=pi)以下为针对二分类任务的评价指标
-
精度(Precision):预测为正例的样本中有多少确为正例
P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP+FP} Precision=TP+FPTP -
召回率(Recall):找到的真实正例占所有正例中的比例
R e c a l l = T P T P + F N Recall = \frac{TP}{TP+FN} Recall=TP+FNTP -
加权调和平均 F β F_\beta Fβ:
F β = 1 / [ 1 1 + β 2 ( 1 P + β 2 R ) ] F 1 = 2 P R P + R F_\beta=1/[\frac{1}{1+\beta ^2}(\frac{1}{P}+\frac{\beta^2}{R})]\\ F_1=\frac{2PR}{P+R} Fβ=1/[1+β21(P1+Rβ2)]F1=P+R2PR -
ROC曲线:表示在不同阈值下模型的真阳性率(TPR)和假阳性率(FPR)之间的关系。
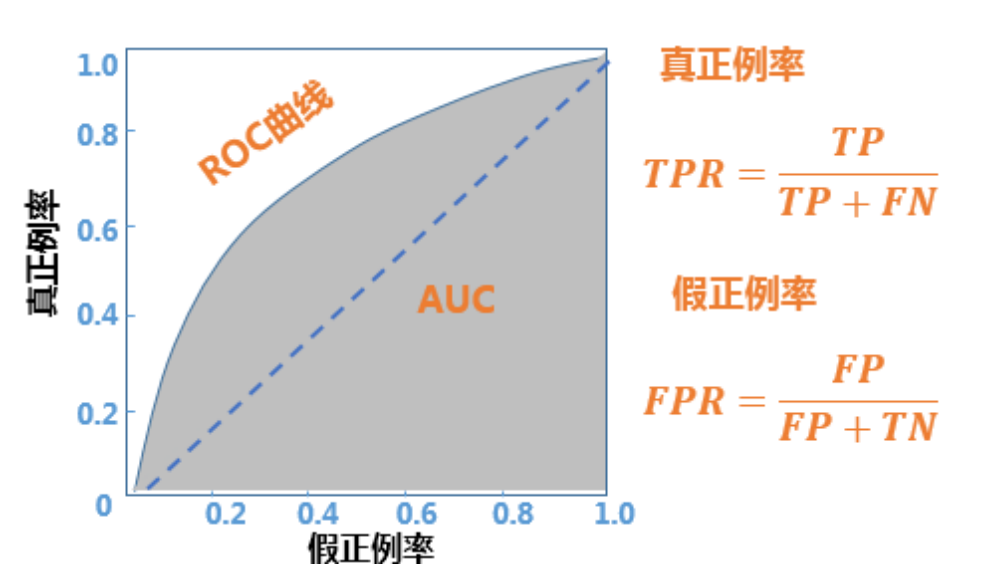
- 根据预测值对样本排序
- 以该样本的预测值为阈值
- 大于或等于阈值记正例,否则记负例可得到一组结果及评价指标,共有样本数n组结果
- 假正例率(False Positive Rate,FPR)为横轴
- 真正例率(True Positive Rate,TPR,也即召回率)为纵轴
-
AUC(Area Under ROC Curve):ROC曲线下的面积,越大越好
- 把测试样例以预测值从大到小排序,其中有n1个真实正例,n0个真实负例
- 设 r i r_i ri 为第 i i i 个真实负例的秩(排序位置), S 0 = ∑ r i S_0=\sum r_i S0=∑ri
A U C = S 0 − n 0 ( n 0 + 1 ) / 2 n 0 N 1 AUC=\frac{S_0-n_0(n_0+1)/2}{n_0N_1} AUC=n0N1S0−n0(n0+1)/2

-
-
特定任务:
-
个性化推荐:前K项精度(Precision@K)、前K项召回率(Recall@K)、前K项 命中率(Hit@K)等
-
对话系统:BLEU、ROUGE、METEOR等
-
DCG(Discounted Cumulative Gain):DCG 是对一个特定位次p的累积增益(Cumulative)
-
2.2 训练集、验证集与测试集
- 训练集:模型可见样本标签,用于训练模型,样本数有限
- 测试集:用于评估模型在可能出现的未见样本上的表现
- 验证集:从训练集中额外分出的集合,一般用于超参数的调整(防止过拟合)

2.3 随机重复实验
- 数据随机性:由数据集划分带来的评价指标波动
- (数据足够多时)增多测试样本
- (数据量有限时)重复多次划分数据集
- 模型随机性:由模型或学习算法本身带来的评价指标波动
- 更改随机种子重复训练、测试
- 报告结果:评价指标的均值 X ˉ = 1 n ∑ i = 1 n X i \bar X=\frac{1}{n}\sum_{i=1}^{n}X_i Xˉ=n1∑i=1nXi
- 样本标准差(个体离散程度,反映了个体对样本均值的代表性) S = ∑ i = 1 n ( X i − X ˉ ) 2 / ( n − 1 ) S=\sqrt{\sum_{i=1}^{n}(X_i-\bar X)^2/(n-1)} S=∑i=1n(Xi−Xˉ)2/(n−1)
- 标准误差(样本均值的离散程度,反映了样本均值对总体均值的代表性) S E M = S n SEM=\frac{S}{\sqrt{n}} SEM=nS
注意:保持每次得到的评价指标独立同分布(iid)
2.4 K折交叉验证
随机把数据集分成K个相等大小的不相交子集,K一般取5、10

- 优点:数据利用率高,适用于数据较少时
- 缺点:训练集互相有交集,每一轮之间并不满足独立同分布
- 增大K,一般情况下:
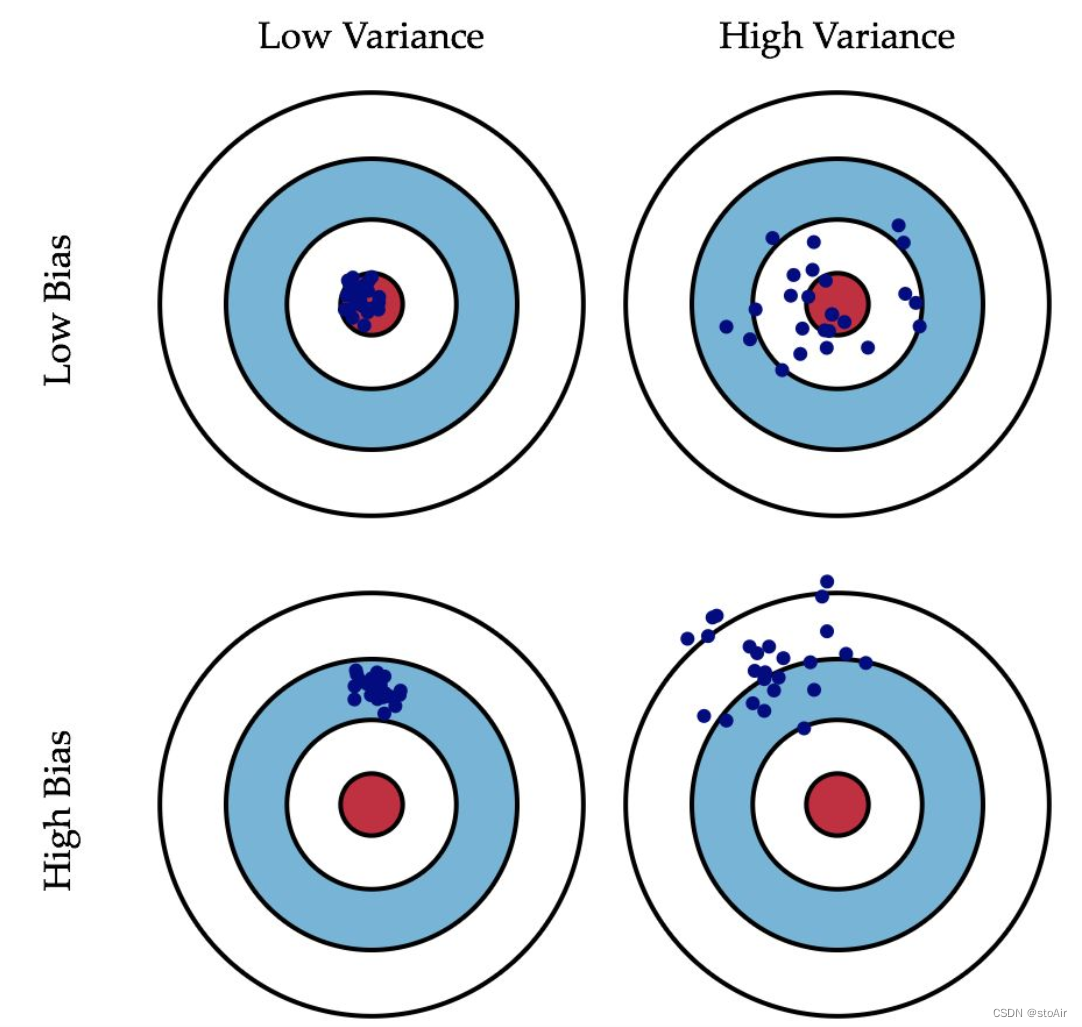
- 所估计的模型效果偏差(bias)下降
- 所估计的模型效果方差(variance)上升
- 计算代价上升,更多轮次、训练集更大
2.4 统计有效性检验
-
抽样理论基础
二项分布:描述了在n次次独立的伯努利试验中,成功的次数的离散情况。
伯努利试验:成功概率: p,失败概率: q =1-p;n次试验中正好得到r次成功的概率为P®。
P ( r ) = C n r p r ( 1 − p ) n − r = n ! r ! ( n − r ) ! p r ( 1 − p ) n − r P(r)=C_n^rp^r(1-p)^{n-r}=\frac{n!}{r!(n-r)!}p^r(1-p)^{n-r} P(r)=Cnrpr(1−p)n−r=r!(n−r)!n!pr(1−p)n−r

-
效果估计
给定一个假设在有限量数据上的准确率,该准确率是否能准确估计在其它未见数据上的效果?
n 个随机样本中有 r 个被误分类的概率——二项分布(样本的错误率=真实的错误率)
真实错误率 e r r o r D ( h ) = p , 样本错误率 e r r o r S ( h ) = r / n E [ r ] = n p , E [ e r r o r S ( h ) ] = E [ r / n ] = p = e r r o r D ( h ) σ e r r o r S ( h ) = σ r n ≈ e r r o r S ( h ) ( 1 − e r r o r S ( h ) ) n 真实错误率error_D(h)=p,样本错误率error_S(h)=r/n\\ E[r]=np,E[error_S(h)]=E[r/n]=p=error_D(h)\\ σ_{error_S(h)}=\frac{σ_r}{n}≈\sqrt{\frac{error_S(h)(1-error_S(h))}{n}} 真实错误率errorD(h)=p,样本错误率errorS(h)=r/nE[r]=np,E[errorS(h)]=E[r/n]=p=errorD(h)σerrorS(h)=nσr≈nerrorS(h)(1−errorS(h))
样本期望值=真实期望值;样本方差值 ≈ 真实方差值-
估计**偏差 (Bias)**
如果 S 是训练集, e r r o r S ( h ) error_S (h) errorS(h) 是有偏差的,bias指样本错误率的期望与真实错误率的差值
bias = E [ error S ( h ) ] − error D ( h ) \text{bias}=E[\text{error}_S(h)]-\text{error}_D(h) bias=E[errorS(h)]−errorD(h)
对于无偏估计(bias =0), h(训练集模型)和 S(测试集)必须独立不相关地产生——不要在训练集上测试! -
估计**方差 (Varias)**
即使是S 的无偏估计, e r r o r S ( h ) error_S (h) errorS(h) 可能仍然和 e r r o r D ( h ) error_D (h) errorD(h) 不同,例:n=100,r=12;n=25,r=3错误率都为12%,但是方差分别为3.2%,6.5%
需要选择无偏的且有最小方差的估计
-
-
置信区间——准确率的估计可能包含多少错误?
定义:参数p 的N %置信区间是一个以N %的概率包含p 的区间, N% : 置信度
90.0%的置信度 ,年龄:[12, 24]
99.9%的置信度,年龄:[3, 60]
-
如何得到置信区间?——通过正态分布的某个区间 (面积)来获得
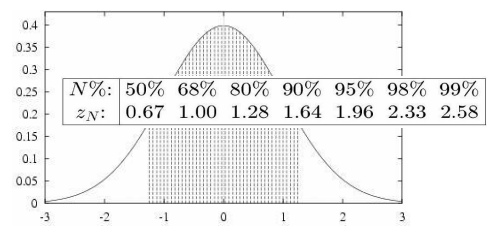
均值 μ μ μ有N%的可能性落在区间 y ± Z N σ y±Z_Nσ y±ZNσ
-
中心极限定理——当样本量足够大时,二项分布可以用正态分布来近似。
经验法则: n > 30 , n p ( 1 − p ) > 5 n>30, np(1-p)> 5 n>30,np(1−p)>5
问题设定:
a. 独立同分布的随机变量 Y 1 , . . . , Y n Y_1,...,Y_n Y1,...,Yn;
b. 未知分布,有均值 μ \mu μ和有限方差 σ 2 \sigma^2 σ2;
c. 估计均值为 Y ˉ = 1 n ∑ i = 1 n Y i \bar Y=\frac{1}{n}\sum_{i=1}^nY_i Yˉ=n1∑i=1nYi,服从正态分布
若S 包含 n >= 30个样本, 与h独立产生,且每个样本独立采样,则真实错误率 e r r o r D error_D errorD落在以下区间有N% 置信度:
e r r o r S ( h ) ± z N e r r o r S ( h ) ( 1 − e r r o r S ( h ) ) n error_S(h)±z_N\sqrt{\frac{error_S(h)(1-error_S(h))}{n}} errorS(h)±zNnerrorS(h)(1−errorS(h))
-
-
假设检验
比较两个样本或一个样本和一个常数的均值差异是否显著
-
z检验
Z检验通常用于大样本(样本容量大于30)或已知总体标准差的情况。Z值的计算方式为:
Z = X ˉ − μ σ n Z = \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}} Z=nσXˉ−μ
- X ˉ \bar{X} Xˉ 是样本均值。
- μ \mu μ是总体均值。
- σ \sigma σ是总体标准差。
- n n n 是样本容量。
一般用于单次评测,随机变量为每个测试样本的对错
-
t检验
t检验适用于小样本(样本容量小于30)或总体标准差未知的情况。t值的计算方式为:
t = X ˉ − μ s n t = \frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}} t=nsXˉ−μ- X ˉ \bar{X} Xˉ 是样本均值。
- μ \mu μ是总体均值。
- s s s是样本标准差。
- n n n 是样本容量。
一般用于多次评测如重复实验,随机变量为每次测试集上的指标
-