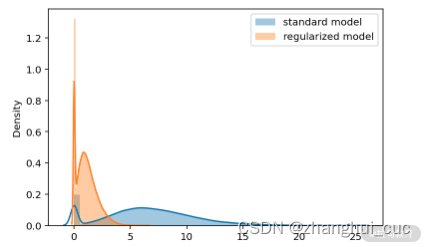
时频分析相较于目前的时域、频域信号处理方法在分析时变信号方面,其主要优势在于可以同时提供时域和频域等多域信号信息,并清晰的刻画了频率随时间的变化规律,已被广泛用于医学工程、地震、雷达、生物及机械等领域。
线性时频分析方法是将信号分解为时域和频域中基的加权和,例如短时傅里叶变换STFT和小波变换WT。短时傅里叶变换利用短窗口沿时间尺度移动以对信号进行切片,可以获得每个片段的局部傅里叶谱,揭示信号的变化规律。由于海森堡不确定原理,STFT方法在达到最优时间位置时其时频分辨率较低,反之亦然。因此,该方法缺乏适应性,它只适用于分析在短时间窗尺度上的平稳信号,而不适用于分析信号中的高瞬态冲击信号。小波变换是一种重要的信号处理工具,利用可变窗同时兼顾高低频信号的分辨率,适用于非平稳信号分析。但也存在不足之处,小波变换对低频信号进行迭代分解,而对高频的细节信号没有进一步的处理。对于高频分量,小波变换具有较好的时间局域特性,但无法满足最佳频率分辨率的要求;对于低频分量,当达到最优频率分辨率时,而时间局部特性呈现出较差的状态。此外,小波变换还存在与母小波选择标准、边界失真、能量泄漏相关的问题。
二次时频分布主要属于Cohen类双线性时频能量分布,其中最常用的是Wigner-Ville分布及其变体。二次时频分布不包含任何窗函数,因此不受不确定性的影响,但是其交叉项在处理多分量信号中产生较大的影响。尽管这种干扰可以通过平滑处理来减弱,但平滑后的分布会变得模糊,降低时频分辨率。二次时频分析方法的理论中尽管有许多优良的性质,但是由于不能直接重构信号,限制了在实际问题中的应用。
为了提高时频分析的质量,众多学者已经开发了一些时频重分配方法。时频重分配方法是通过修改原始谱能量分布来提高原始线性或二次时频变换的可读性的后处理技术。重新分配后,频谱能量将集中在瞬时频率附近,避免了人为干预。Daubechies和Oberlin分别基于CWT和STFT提出了同步压缩变换SST。
SST方法是通过将时频系数压缩至瞬时频率的轨迹中进行设计的,提高了时频的分辨率并重建了原始信号。但在强噪声的干扰下SST方法的时频分辨率较低,并且由于其对真实瞬时频率分布的估计偏差而导致时频能量不集中。
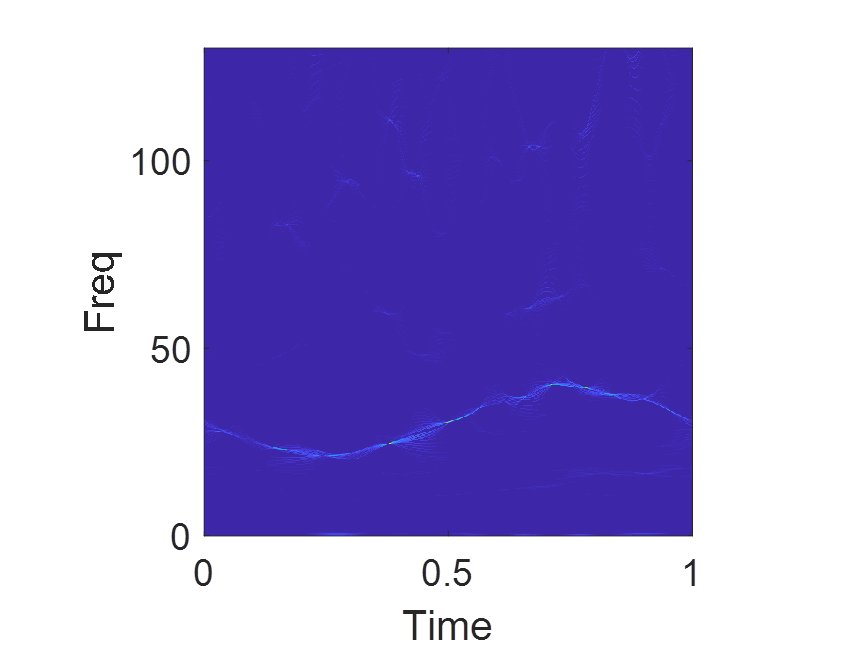
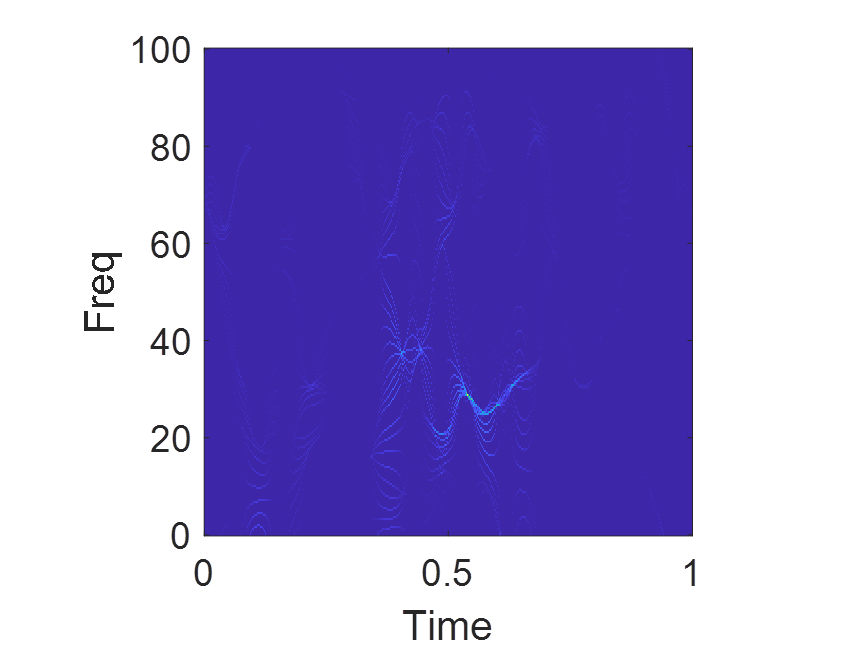
同步压缩小波包变换方法首先将信号进行小波包变换得到小波包变换系数,然后求取信号的瞬时频率,最后对小波包变换系数沿信号瞬时频率方向进行压缩,从而将各频率成分清晰呈现于时频图中,可以提高时频分辨率。
程序运行环境为MATLAB R2018A,执行一维时间序列信号的同步压缩小波包变换,并给出了模拟信号和实际信号的例子。算法可迁移至金融时间序列,地震信号,语音信号,声信号,生理信号等一维时间序列信号。
部分代码如下:
% Inputs
% x input signal, a vector of length N
%
% Optional Inputs
% is_real Type of the transform
% 0: complex-valued wave packets
% 1: real-valued wave packets
% [default set to 0]
% is_unif whether x is sampled on a uniform grid
% 0: No; 1: Yes
% typeNUFFT 1: NUFFT by Air Force Lab
% 2: USFFT by E. Candes
% 3: NUFFT by L. Greengard and J.-Y. Lee
% 4: Direct non-uniform Fourier Transform
% xo non-uniform locations at which x is measured
% NG number of subsampled points in time
% [R_low R_high] The range of interested spectrum
% rad a parameter to adjust the size of supports of the mother wave packet in
% the frequency domain, rad <= 2.
% is_cos Type of the window function
% 0: C^infinity window function
% 1: cosine window function
% [default set to 0]
% t_sc scaling parameter for radius
% [default set to 1-1/4]
% red redundancy parameter, red is a positive integer
% [default set to 1]
% epsl threshold for instantaneous frequency estimates
% [default set to 1e-2]
% h frequency band width per pixel in the synchrosqueezed
% time-frequency representation
% [default set to 1]
% is_fac 0: do not increase the magnitude of high frequency wave
% packet coefficients; 1: increase;
% [default set to 1, better to visualize high frequency
% instantaneous frequencies]
% wedge_length_coarse
% length of coarsest wedge
% [default set to 4]
%
% Outputs
% T_f 1D synchrosqueezed wave packet transform, a matrix with NG columns, each column represent frequency
% information at a fixed time
% coef 1D wave packet transform coefficients of x
% kk instantaneous frequency estimates from each wave packet
% coefficient出图如下: