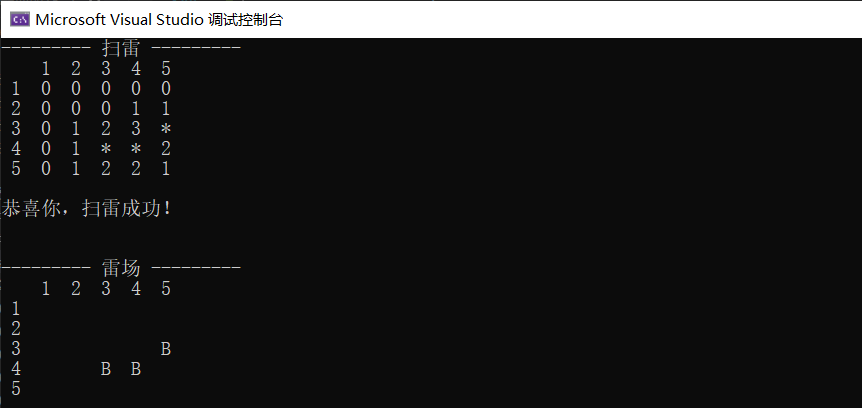
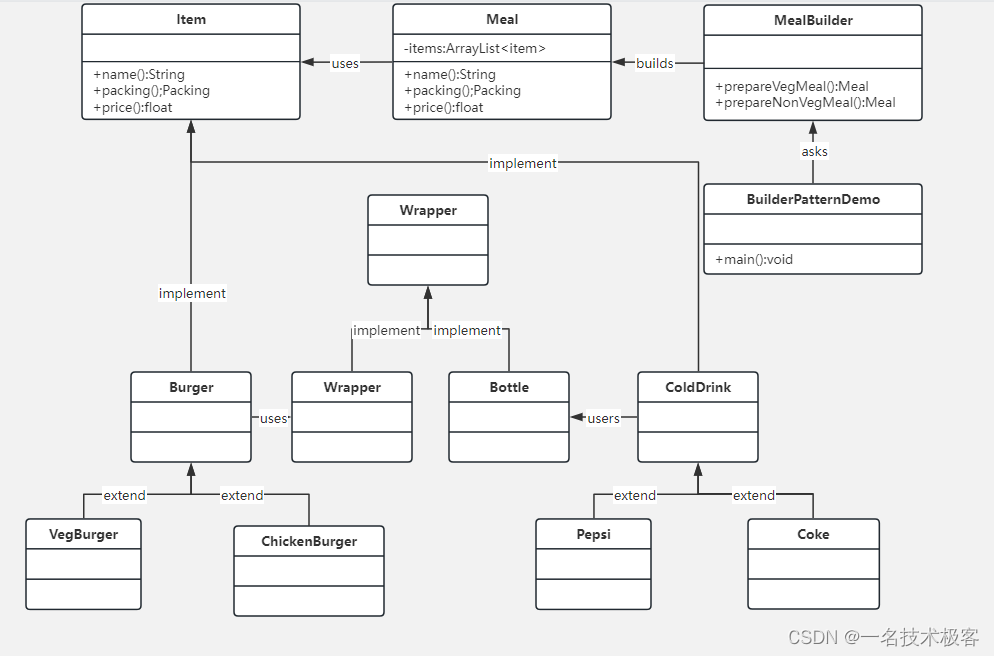
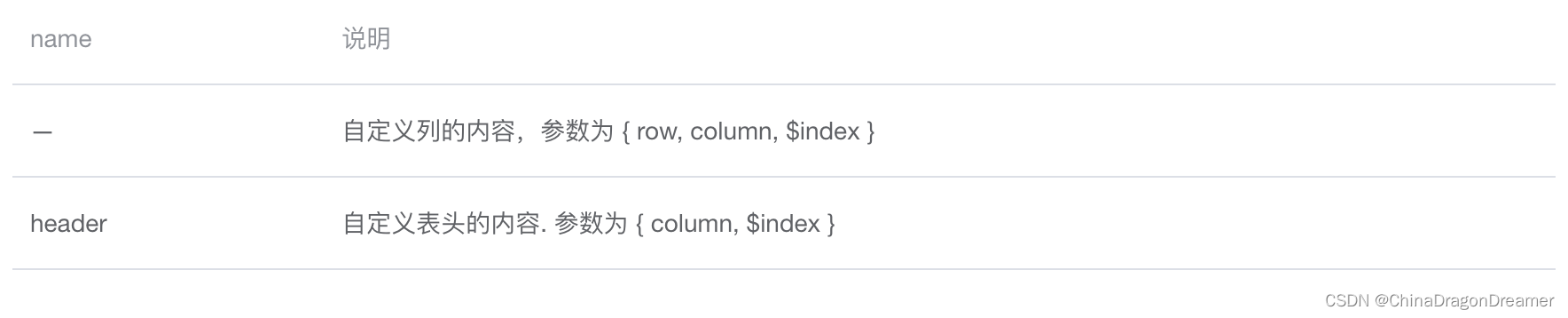
Kmeans算法中K值的确定是很重要的。
下面利用python中sklearn模块进行数据聚类的K值选择
数据集自制数据集,格式如下:

维度为3。
①手肘法
手肘法的核心指标是SSE(sum of the squared errors,误差平方和),

其中,Ci是第i个簇,p是Ci中的样本点,mi是Ci的质心(Ci中所有样本的均值),SSE是所有样本的聚类误差,代表了聚类效果的好坏。
手肘法的核心思想是:随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。并且,当k小于真实聚类数时,由于k的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大,而当k到达真实聚类数时,再增加k所得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减,然后随着k值的继续增大而趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,而这个肘部对应的k值就是数据的真实聚类数。当然,这也是该方法被称为手肘法的原因。
python代码:
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import xlrd
rawData = xlrd.open_workbook('kmeansdata.xlsx')
table = rawData.sheets()[0]
data = []
for i in range(table.nrows):if i == 0:continueelse:data.append(table.row_values(i)[1:])
featureList = ['Age', 'Gender', 'Degree']
mdl = pd.DataFrame.from_records(data, columns=featureList)
SSE = []
for k in range(1, 9):estimator = KMeans(n_clusters=k) estimator.fit(np.array(mdl[['Age', 'Gender', 'Degree']]))SSE.append(estimator.inertia_)
X = range(1, 9)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X, SSE, 'o-')
plt.show()
效果图:
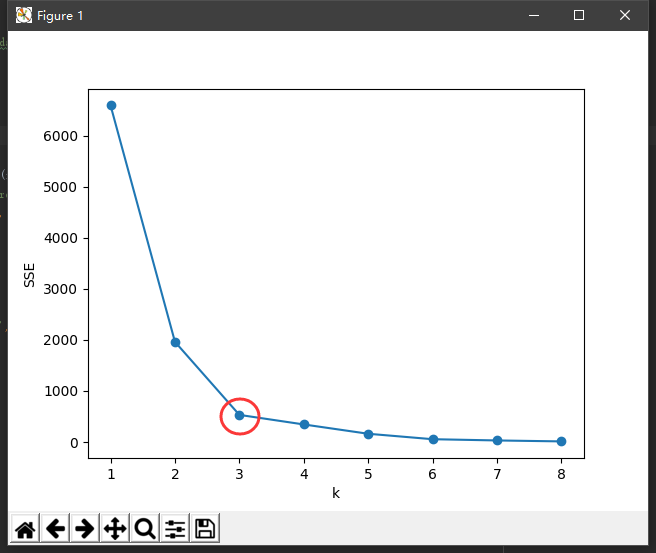
显然,肘部对于的k值为3,故对于这个数据集的聚类而言,最佳聚类数应该选3。
②轮廓系数法
该方法的核心指标是轮廓系数(Silhouette Coefficient),某个样本点Xi的轮廓系数定义如下:
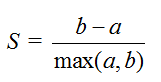
其中,a是Xi与同簇的其他样本的平均距离,称为凝聚度,b是Xi与最近簇中所有样本的平均距离,称为分离度。而最近簇的定义是
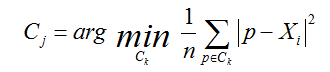
其中p是某个簇Ck中的样本。事实上,简单点讲,就是用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后,选择离Xi最近的一个簇作为最近簇。
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1],且簇内样本的距离越近,簇间样本距离越远,平均轮廓系数越大,聚类效果越好。那么,很自然地,平均轮廓系数最大的k便是最佳聚类数。
python代码:
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
import xlrd
rawData = xlrd.open_workbook('kmeansdata.xlsx')
table = rawData.sheets()[0]
data = []
for i in range(table.nrows):if i == 0:continueelse:data.append(table.row_values(i)[1:])
featureList = ['Age', 'Gender', 'Degree']
mdl = pd.DataFrame.from_records(data, columns=featureList)Scores = []
for k in range(2, 9):estimator = KMeans(n_clusters=k) estimator.fit(np.array(mdl[['Age', 'Gender', 'Degree']]))Scores.append(silhouette_score(np.array(mdl[['Age', 'Gender', 'Degree']]), estimator.labels_, metric='euclidean'))
X = range(2, 9)
plt.xlabel('k')
plt.ylabel('轮廓系数')
plt.plot(X, Scores, 'o-')
plt.show()
效果图:
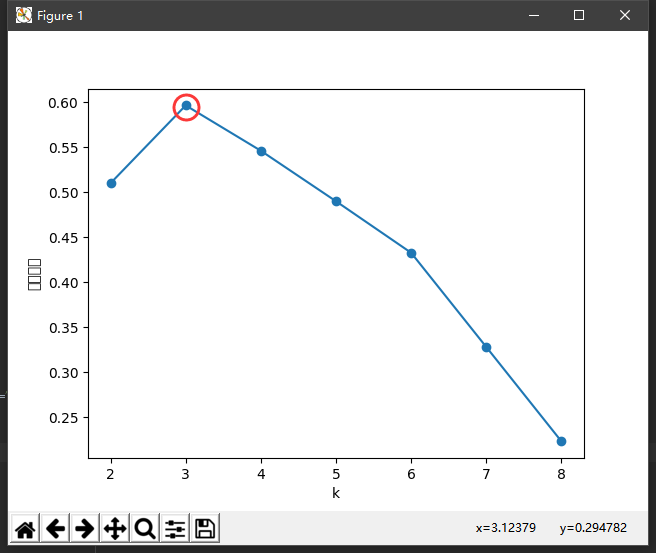
可以看到,轮廓系数最大的k值是3,这表示我们的最佳聚类数为3。
说明:建议比较两个方法选出的K值,如果没有特殊情况的话,建议首先考虑用手肘法。
参考资料:https://blog.csdn.net/qq_15738501/article/details/79036255



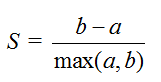
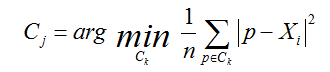


![[office] 怎么在Excel2003菜单栏自定义一个选项卡 #其他#微信#知识分享](https://img-blog.csdnimg.cn/img_convert/55b73e208349e2367688f1525240527f.jpeg)