目录
参考资料
顺序栈的实现
头文件SqStack.h(顺序栈函数声明)
源文件SqStack.cpp(顺序栈函数实现)
顺序栈的三个应用
数值转换
行编辑程序
顺序栈的实现测试
栈与递归的实现(以汉诺塔为例)
参考资料
1.本文文章结构参考这篇博客,部分代码也引用自这篇博客。
2021-9-22【数据结构/严蔚敏】【顺序栈&链式栈&迷宫求解&表达式求值】【代码实现算法3.1-3.5】_数据结构表达式求值代码严老师-CSDN博客
2.又搜到一个更靠谱的,这个的引用也用指针替代了。
栈和队列-数据结构与算法(C语言版)_调用pop(&s,&e)函数,让队头数据出队,赋值给参数e,printf输出e-CSDN博客3. 数据结构课本严蔚敏版。
顺序栈的实现
头文件SqStack.h(顺序栈函数声明)
#pragma once
#include <cstdio>
#include <cstdlib>
#include <cstring>#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;//Status是函数的类型,其值是函数结果状态代码
typedef int SElemType;//-----栈的顺序存储表示-----
#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量
typedef struct SqStack {SElemType* base;//在栈构造之前和销毁之后,base的值为NULLSElemType* top; //栈顶指针int stacksize; //当前已分配的存储空间,以元素为单位
}SqStack;
//-----基本操作的函数原型说明-----
Status InitStack(SqStack& S);
//构造一个空栈S
Status DestroyStack(SqStack& S);
//销毁栈S,S不再存在
Status ClearStack(SqStack& S);
//把S置为空栈
Status StackEmpty(SqStack S);
//若栈S为空栈,则返回TRUE,否则返回FALSE
int StackLength(SqStack S);
//返回S的元素个数,即栈的长度
Status GetTop(SqStack S, SElemType& e);
//若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR
Status Push(SqStack& S, SElemType e);
//插入元素e为新的栈顶元素
Status Pop(SqStack& S, SElemType& e);
//若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR
Status StackTraverse(SqStack S, void(*visit)(SElemType));
//从栈顶到栈底依次对栈中每个元素调用函数visit()。一旦visit()失败,则操作失败
源文件SqStack.cpp(顺序栈函数实现)
源文件SqStack.cpp是头文件SqStack.h的实现。
#include "SqStack.h"//-----基本操作的函数算法描述(部分)-----
Status InitStack(SqStack& S) {//构造一个空栈SS.base = (SElemType*)malloc(STACK_INIT_SIZE * sizeof(SElemType));if (!S.base)exit(OVERFLOW);//存储分配失败,警告C6011S.top = S.base;S.stacksize = STACK_INIT_SIZE;return OK;
}Status DestroyStack(SqStack& S) {free(S.base);S.top = S.base = NULL;S.stacksize = 0;return OK;
}Status ClearStack(SqStack& S) {if (!S.base)return ERROR;S.top = S.base;return OK;
}Status StackEmpty(SqStack S) {if (S.base == S.top)return OK;return ERROR;
}int StackLength(SqStack s) {if (!s.base)return ERROR;return (int)(s.top - s.base);
}Status GetTop(SqStack s, SElemType& e) {//若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERRORif (s.base == s.top)return ERROR;e = *(s.top - 1);return OK;
}Status Push(SqStack& s, SElemType e) {//插入元素e为新的栈顶元素if (!s.base)return ERROR;if (s.top - s.base >= s.stacksize) {//栈满,追加存储空间s.base = (SElemType*)realloc(s.base, (s.stacksize + STACKINCREMENT) * sizeof(SElemType));if (!s.base)exit(_OVERFLOW);//存储分配失败s.top = s.base + s.stacksize;s.stacksize += STACKINCREMENT;}*s.top++ = e;//*s.top=e; s.top++;return OK;
}Status Pop(SqStack& s, SElemType& e) {//若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERRORif (!s.base || s.top == s.base) return ERROR;e = *--s.top;//--s.top; e=*s.top;return OK;
}Status StackTraverse(SqStack s, void (*visit)(SElemType)) {SElemType* p = s.base;if (!s.base)return ERROR;while (p < s.top)visit(*p++);printf("\n");return OK;
}顺序栈的四个应用
数值转换
源文件conversion.cpp
#include "SqStack.h"void conversion() {//对于输入的任意一个非负十进制整数,打印输出与其等值的八进制数SqStack S;InitStack(S);//构造空栈SElemType N,e;scanf_s("%d", &N);if (N == 0)//当N为0时下面的while循环不输出{printf("%d", N);return;}while (N) {Push(S, N % 8);N = N / 8;}while (!StackEmpty(S)) {Pop(S, e);printf("%d", e);}
}
int main()
{conversion();return 0;
}//算法3.1测试结果(课本样例)

括号匹配
栈和队列-数据结构与算法(C语言版)_调用pop(&s,&e)函数,让队头数据出队,赋值给参数e,printf输出e-CSDN博客源文件 MatchBrackets.cpp
完整代码
#include "SqStack.h"/** 括号匹配* 注意将ElemType 修为 char*/
Status MatchBrackets(SqStack& S, char* brackets) {SElemType ch;int len = strlen(brackets);for (int i = 0; i < len; i++) {if (brackets[i] == '{' || brackets[i] == '[' || brackets[i] == '(') {Push(S, brackets[i]);}if (brackets[i] == '}' || brackets[i] == ']' || brackets[i] == ')') {if (StackEmpty(S)) {printf("右括号多于左括号\n");return ERROR;}else {GetTop(S, ch);if (ch == '{' && brackets[i] == '}' || ch == '[' && brackets[i] == ']' || ch == '(' && brackets[i] == ')') {Pop(S, ch);}}}}if (!StackEmpty(S))printf("左括号多于右括号\n");elseprintf("括号匹配成功!");return OK;
}int main()
{SqStack S;char brackets[81] = { 0 };//用char* brackets;会报错InitStack(S);scanf_s("%s", brackets,sizeof(brackets));//不知道为什么,不加sizeof(),括号匹配函数len一直为0,//导致输出总是“括号匹配成功”。MatchBrackets(S, brackets);return 0;
}
测试结果




行编辑程序
源文件LineEdit.cpp
本来想两个主函数能不能在同一个工程下运行,结果不可以。接着我把数值转换这个主函数移除,发现可以运行行编辑程序这个代码了。
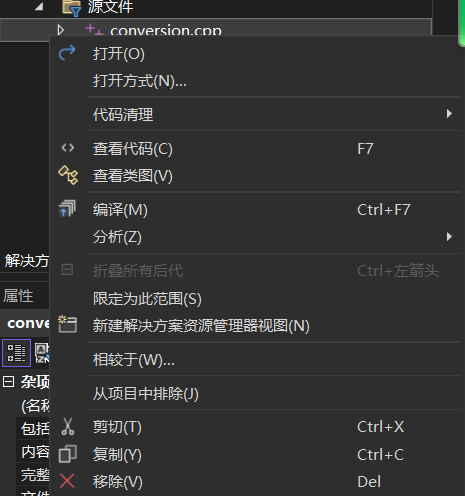
右键conversion.cpp,点击移除。
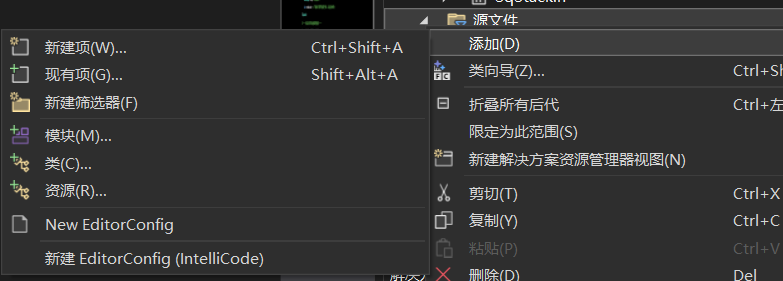
接着打开LineEdit.cpp。右键点击源文件,在添加中找到现有项,点击现有项寻找即可(前提是你写了)

下面是完整代码
#include "SqStack.h"void visit(SElemType e) {printf("%d ", e);
}void LineEdit() {//利用字符栈S,从终端接收一行并传送至调用过程的数据区SqStack S;InitStack(S);//构造空栈SSElemType c;char ch = getchar();//从终端接收第一个字符while (ch != EOF) {//EOF为全文结束符,Ctrl+z+回车键对应EOFwhile (ch != EOF && ch != '\n') {//一行内switch (ch) {case'#':Pop(S, c);break;//仅当栈非空时退栈case'@':ClearStack(S);break;//重置S为空栈default:Push(S, ch);break;//有效字符进栈,未考虑栈满情形}ch = getchar();//从终端接收下一个字符}//将从栈底到栈顶的栈内字符传送至调用过程中的数据区StackTraverse(S, visit);//课本没有,但我看不到结果,便加上了这个函数ClearStack(S);//重置S为空栈if (ch != EOF)ch = getchar();}DestroyStack(S);
}
int main()
{LineEdit();return 0;
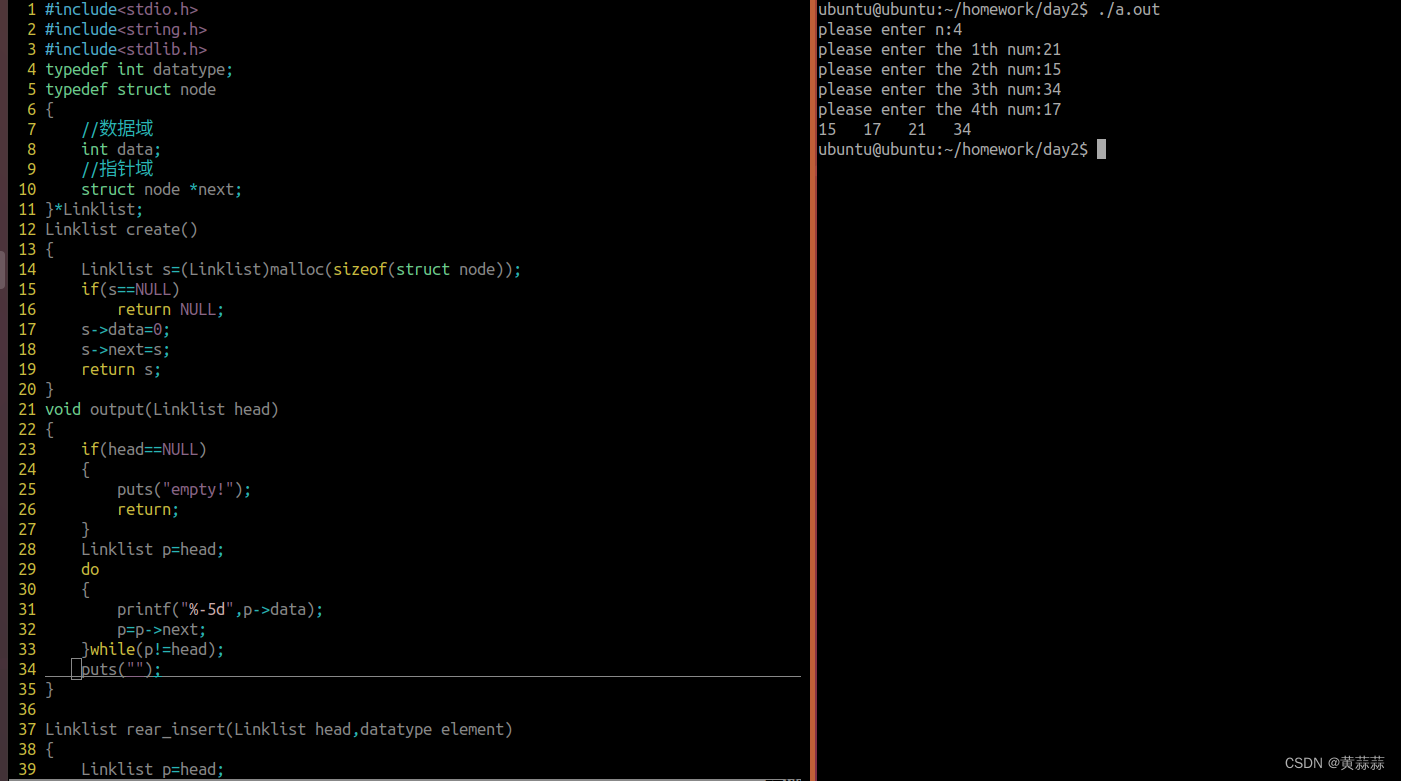
}测试样例选自课本P49页右下角两行字符,测试结果如下:

此时正常返回。从元素个数看,结果正确,但不直观,所以将SElemType改为char类型。
为了实现行编辑程序,特别修改两处代码(仅在行编辑程序中使用)。
typedef char SElemType;//修改SqStack.h第13行void visit(SElemType e) {printf("%c", e);
}//修改LineEdit.cpp第4行最终结果

顺序栈的实现测试
源文件test.cpp ,这个是我复制粘贴的我参考的博客。
#include "SqStack.h"
#include <iostream>
using namespace std;void visit(SElemType e) {printf("%d ", e);
}
//简单测试主函数
int main() {SqStack s;cout << "InitStack" << endl;InitStack(s);cout << "StackEmpty" << endl;StackEmpty(s) ? cout << "yes\n" : cout << "no\n";cout << "Push" << endl;for (int i = 1; i <= 6; i++)Push(s, i);cout << "StackTraverse" << endl;StackTraverse(s, visit);cout << "StackLength" << endl;cout << StackLength(s) << endl;cout << "Pop" << endl;SElemType e;Pop(s, e);cout << e << endl;StackTraverse(s, visit);cout << "GetTop" << endl;GetTop(s, e);cout << e << endl;return 0;
}测试结果

栈与递归的实现(以汉诺塔为例)
这里课本的代码没有用栈实现递归,但一直在强调递归函数是通过栈实现的,并从栈的角度解释了递归函数的原理。
源文件hanoi.cpp
#include <cstdio>
#include <cstdlib>
#include <cstring>int C = 0;
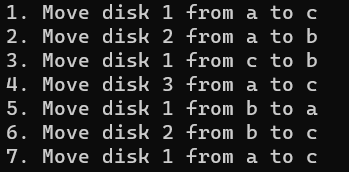
void move(char x, int n, char z) {printf("%d. Move disk %d from %c to %c\n", ++C, n, x, z);
}
void hanoi(int n, char x, char y, char z)
//将塔座x上按直径由小到大且自上而下编号为1至n的n个圆盘按规则搬到
//塔座z上,y可用作辅助塔座。
//搬动操作move(x, n, z) 可定义为(c是初值为0的全局变量,对搬动计数):
//printf(" %i. Move disk %i from %c to %c\n", ++c, n, x, z);
{if (n == 1)move(x, 1, z);//将编号为1的圆盘从x移到zelse {hanoi(n - 1, x, z, y);//将x上编号为1至n-1的圆盘移到y,z作辅助塔move(x, n, z); //将编号为n的圆盘从x移到zhanoi(n - 1, y, x, z);//将y上编号为1至n-1的圆盘移到z,x做辅助塔}
}
int main()
{int n=3;char A='a', B='b', C='c';hanoi(n, A, B, C);return 0;
}