随机过程论就是研究随时间变化的动态系统中随机现象的统计规律的一门数学学科。
目录
前言
一、随机过程的定义及分类
1、定义
2、分类
二、随机过程的分布及其数字特征
1、分布函数
2、数字特征
均值函数和方差函数
协方差函数和相关函数
3、互协方差函数与互相关函数
三、复随机过程
总结
前言
随机过程理论产生于本世纪初,起源于统计物理学领域。布朗运动和热噪声是随机过程的最早例子。随机过程理论在社会科学、自然科学和工程技术的各个领域中都有着广泛的应用。例如:现代电子技术、现代通讯、自动控制、系统工程的可靠性工程、市场经济的预测和控制、随机服务系统的排队论﹑储存论、生物医学工程、人口的预测和控制等等。只要人们要研究随时间变化的动态系统的随机现象的统计规律时,就要应用到随机过程的理论。
一、随机过程的定义及分类
1、定义
随机过程可以形式化地定义为一个随机变量的集合 {X(t), t ∈ T},其中 T 是一个表示时间的参数集合。对于每个时间点 t ∈ T,X(t) 是一个随机变量,表示在该时间点上观察到的随机现象的取值。这样的集合 {X(t), t ∈ T} 被称为随机过程。
在实际应用中,随机过程通常分为离散时间和连续时间两种情况。如果参数集合 T 是离散的,那么随机过程是离散时间随机过程;如果参数集合 T 是连续的,那么随机过程是连续时间随机过程。
随机过程的性质可以通过其概率分布、相关性函数、平均值等统计量来描述,这些性质可以用来分析随机过程的行为和特征。 常见的随机过程包括布朗运动、泊松过程、马尔可夫过程等。

说明:{X(t,),t e T}
- 参数集T在实际问题中,常常指的是时间参数,但有时也用其它物理量作为参数集。
- X(t,o)是定义在T×Q上的二元函数。
- t固定时,X(t,o)是随机变量。o固定时,X(t,o)是T的样本函数。
- 随机过程{X(t),t aT}是时刻t上的取值x,称为状态,状态的全体称为状态空间。记为:E={x : X(t)=x,t eT}
2、分类
按状态空间和参数集分类:

按概率分布规律分类:随机过程{X(t),t∈ T}按其概率分布规律分为:独立过程、独立增量过程、正态过程﹑泊松过程、维纳过程﹑平稳过程和马尔可夫过程等等。
二、随机过程的分布及其数字特征
1、分布函数
一维分布函数和一维概率密度是用来描述随机变量的统计性质的工具。它们是概率论中的基本概念,用于描述随机变量在不同取值上的概率分布。
一维分布函数 (Cumulative Distribution Function, CDF):
- 一维分布函数是一个函数,表示随机变量小于或等于某个特定取值的累积概率。
- 用 F(x) 表示,其中 x 是随机变量的某个具体取值。
- 公式:F(x)=P(X≤x)
- 分布函数具有以下性质:
- 0≤F(x)≤1 对所有 x 成立。
- F(x) 是非递减函数,即对于 x1<x2,有 F(x1)≤F(x2)。
- 当x→−∞ 时,F(x)→0,当 x→+∞ 时,F(x)→1。
一维概率密度 (Probability Density Function, PDF):
- 一维概率密度是一个函数,表示随机变量在某个取值附近的概率密度。
- 用 f(x) 表示,其中 x 是随机变量的某个具体取值。
- 公式:f(x)=dxdF(x)
- 概率密度具有以下性质:
- 对于所有 x,f(x)≥0。
- 在整个实轴上的积分等于 1,即∫−∞+∞f(x)dx=1。
- 在某个区间上的概率可以通过概率密度函数在该区间上的积分来计算。
在实际应用中,分布函数和概率密度函数是用来描述随机变量在不同取值上的概率分布特征的重要工具,它们在统计学、概率论、以及随机过程的分析中都有广泛的应用。
二维分布函数 (Joint Cumulative Distribution Function, Joint CDF):
- 对于两个随机变量 X 和 Y,二维分布函数F(x,y) 表示这两个变量小于或等于给定取值的联合累积概率。
- 公式:F(x,y)=P(X≤x,Y≤y)
- 二维分布函数具有类似一维分布函数的性质,包括非递减性和在边界处的收敛性。
二维概率密度 (Joint Probability Density Function, Joint PDF):
- 对于两个随机变量 X 和 Y,二维概率密度函数 f(x,y) 表示在给定点 (x,y) 处的联合概率密度。
- 公式:f(x,y)=∂x∂y∂2F(x,y)
- 二维概率密度函数具有以下性质:
- 对于所有 x 和 y,f(x,y)≥0。
- 在整个二维空间上的积分等于1,即 ∬−∞+∞f(x,y)dxdy=1。
- 对于任意二维区域 A,该区域上的概率可以通过概率密度函数在该区域上的二重积分来计算。
N维分布函数和N维概率密度函数用于描述多个(N个)随机变量的联合概率分布。它们是概率论和统计学中的基本概念,用于研究多个随机变量之间的关系以及它们在不同取值上的概率分布。
N维分布函数 (Joint Cumulative Distribution Function, Joint CDF):
- 对于N个随机变量 X1,X2,…,XN,N维分布函数 F(x1,x2,…,xN) 表示这些变量小于或等于给定取值的联合累积概率。
- 公式:F(x1,x2,…,xN)=P(X1≤x1,X2≤x2,…,XN≤xN)
- N维分布函数具有类似于一维和二维分布函数的性质,包括非递减性和在边界处的收敛性。
N维概率密度函数 (Joint Probability Density Function, Joint PDF):
- 对于N个随机变量 X1,X2,…,XN,N维概率密度函数f(x1,x2,…,xN) 表示在给定点 (x1,x2,…,xN) 处的联合概率密度。
- 公式:f(x1,x2,…,xN)=∂x1∂x2…∂xN∂NF(x1,x2,…,xN)
- N维概率密度函数具有类似于一维和二维概率密度函数的性质,包括非负性和在整个N维空间上的积分等于1。
N+M维分布函数和N+M维概率密度函数是用于描述两组随机变量的联合概率分布。假设有N个变量组成的随机向量 X=(X1,X2,…,XN) 和M个变量组成的随机向量 Y=(Y1,Y2,…,YM),则N+M维分布函数和N+M维概率密度函数描述的是这两组随机变量在一起的联合分布。
N+M维分布函数 (Joint Cumulative Distribution Function, Joint CDF):
- 对于随机向量 X 和 Y,N+M维分布函数 F(x1,x2,…,xN,y1,y2,…,yM) 表示这两个随机向量中的每一个分量小于或等于相应的给定取值的联合累积概率。
- 公式:F(x1,x2,…,xN,y1,y2,…,yM)=P(X1≤x1,X2≤x2,…,XN≤xN,Y1≤y1,Y2≤y2,…,YM≤yM)
N+M维概率密度函数 (Joint Probability Density Function, Joint PDF):
- 对于随机向量 X 和 Y,N+M维概率密度函数f(x1,x2,…,xN,y1,y2,\ldous,yM) 表示在给定点 (x1,x2,…,xN,y1,y2,…,yM) 处的联合概率密度。
- 公式:f(x1,x2,…,xN,y1,y2,…,yM)=∂x1∂x2…∂xN∂y1∂y2…∂yM∂N+MF(x1,x2,…,xN,y1,y2,…,yM)
两个随机过程相互独立意味着它们之间的任何一对随机变量都是独立的。如果有两个随机过程 X(t) 和 Y(t),它们在每个时间点上都有一个随机变量值,那么这两个随机过程相互独立意味着对于任意时刻 t1,t2,…,tn,对应的随机变量X(t1),X(t2),…,X(tn) 与Y(t1),Y(t2),…,Y(tn) 是独立的。
形式化地,两个随机过程 X(t) 和 Y(t) 相互独立可以表示为:
P(X(t1)≤x1,X(t2)≤x2,…,X(tn)≤xn,Y(t1)≤y1,Y(t2)≤y2,…,Y(tn)≤yn) =P(X(t1)≤x1)⋅P(X(t2)≤x2)⋅…⋅P(X(tn)≤xn)⋅P(Y(t1)≤y1)⋅P(Y(t2)≤y2)⋅…⋅P(Y(tn)≤yn)
有限维度特征函数族:
特征函数是概率论中用于描述随机变量分布的一种函数。有限维度特征函数族指的是一个包含有限维度特征函数的集合,通常用于表示多维随机变量的联合分布。
对于一个N维随机向量X=(X1,X2,…,XN),其特征函数定义为:
ϕ(t1,t2,…,tN)=E[ei(t1X1+t2X2+…+tNXN)]
其中 i 是虚数单位。有限维度特征函数族是指由上述特征函数组成的集合,其中 t1,t2,…,tN 可以取任意实数。
分布函数的对称性和相容性:
-
对称性 (Symmetry):
- 如果随机变量 X 的分布函数 FX(x) 满足FX(x)=FX(−x) 对于所有的 x 成立,那么称 X 具有对称分布。这表示分布关于原点对称。
-
相容性 (Compatibility):
- 如果随机变量 X 和 Y 的分布函数分别为FX(x) 和FY(y),那么 X 和 Y 被称为相容的,如果对于所有实数 a 和 b,下面的等式成立:P(aX+b≤y)=FY(ay−b)
- 这表示对于任意实数a 和 b,通过仿射变换aX+b,从 X 的分布可以得到 Y 的分布。
对称性和相容性是概率论中常见的性质,它们在分析随机变量的性质和特征时非常有用。具有对称性的分布在某些情况下能够简化分析,而相容性则提供了一种从一个分布到另一个分布的变换方式。

2、数字特征
大部分随机过程的分布函数难以得到。研究随机过程的数字特征,可以反映出随机过程的局部统计特性。
均值函数和方差函数
均值函数和方差函数是统计学中常用的两个概念,它们用于描述数据分布的特征。
-
均值函数(Mean Function): 均值函数是一种统计量,通常表示一组数据的平均值。计算均值的方法是将所有数据相加,然后除以数据的总个数。均值是数据分布的中心趋势的一种度量,它对于了解数据集中的典型值很有帮助。均值的数学表示为:

其中,xi 表示数据集中的第i个数据点,n 表示数据点的总个数。
-
方差函数(Variance Function): 方差是一种度量数据分散程度的统计量。方差衡量每个数据点与均值的偏离程度,计算方法是将每个数据点与均值的差值的平方相加,然后除以数据点的总个数。方差越大,说明数据点相对于均值的偏离程度越大。方差的数学表示为:
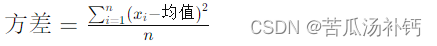
其中,xi 表示数据集中的第i个数据点,均值均值 表示数据的均值,n 表示数据点的总个数。
这两个统计量在分析和描述数据集特征时经常被使用。均值关注数据的中心趋势,而方差关注数据的分散程度。在统计学中,这两者常常一起使用来全面了解数据的分布情况。
在随机过程中,均值函数(Mean Function)和方差函数(Variance Function)描述了随机变量随时间的变化规律。
-
随机过程的均值函数: 随机过程的均值函数表示随机变量在不同时间点的平均值。对于一个离散时间的随机过程,均值函数可以用以下形式表示:
μ(t)=E[X(t)]
其中,X(t) 是随机过程在时刻t 的随机变量,μ(t) 表示在时刻 t 的均值函数,E[⋅] 表示期望运算符。均值函数描述了随机过程在不同时间点的平均趋势。
-
随机过程的方差函数: 随机过程的方差函数表示随机变量在不同时间点的方差。对于一个离散时间的随机过程,方差函数可以用以下形式表示:

其中,X(t) 是随机过程在时刻 t 的随机变量,σ2(t) 表示在时刻 t 的方差函数,Var[⋅] 表示方差运算符。方差函数描述了随机过程在不同时间点的波动性或分散程度。
这些函数对于理解随机过程的特性和性质非常重要。它们提供了关于随机变量随时间演化的一些基本统计信息,有助于建立模型、预测未来状态以及进行随机过程的分析。在实际应用中,通常需要通过采样或模拟来估计这些函数,因为真实的随机过程可能无法直接观测。
均方差函数(Mean-Square Function): 均方差函数是一个衡量随机过程在不同时间点的均方差(平均方差)的函数。对于一个随机过程 X(t),其均方差函数通常用以下形式表示:
![]()
其中,RX(t,τ) 表示在时刻 t 和 t+τ 的均方差函数,E[⋅] 表示期望运算符。均方差函数测量了不同时刻的随机变量之间的平方关系。
协方差函数和相关函数
-
协方差函数(Covariance Function): 协方差函数描述了随机过程在不同时间点的协方差。对于一个随机过程 X(t),其协方差函数通常用以下形式表示:

协方差函数可以用来研究随机过程中不同时刻的随机变量之间的线性关系。
-
相关函数(Correlation Function): 相关函数是一种描述随机过程中不同时刻随机变量之间相关性的函数。对于一个随机过程 X(t),其相关函数通常用以下形式表示:

其中,ρX(t,τ) 表示在时刻 t 和 t+τ 的相关函数,CX(t,τ) 是协方差函数,RX(t,0) 和 RX(t+τ,0) 是均方差函数。
3、互协方差函数与互相关函数
随机过程的互协方差函数和互相关函数描述了两个不同随机过程之间的关系,而不是同一个随机过程在不同时间点的关系。
-
互协方差函数(Cross-Covariance Function): 互协方差函数是用于描述两个不同随机过程之间协方差的函数。如果有两个随机过程 X(t) 和Y(t),它们在时刻 t 和 t+τ 的互协方差函数通常表示为:
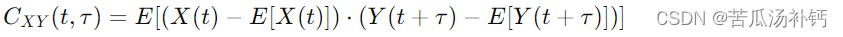
这个函数测量了两个随机过程在不同时刻的随机变量之间的线性关系。
-
互相关函数(Cross-Correlation Function): 互相关函数是用于描述两个不同随机过程之间相关性的函数。如果有两个随机过程 X(t) 和 Y(t),它们在时刻 t 和 t+τ 的互相关函数通常表示为:

其中,CXY(t,τ) 是互协方差函数,RX(t,0) 和 RY(t+τ,0) 分别是 X(t) 和 Y(t) 的均方差函数。
三、复随机过程
复随机过程是一种随机过程,其样本函数(随机过程的每个具体实现)的值是复数。与实数值的随机过程不同,复随机过程的样本函数在每个时间点处都取复数值。
复随机过程通常用以下形式表示:
X(t,ω):Ω×T→C
其中,X(t,ω) 是复随机过程的样本函数,Ω 是样本空间,T 是时间集合,ω 是样本点,t 是时间。复随机过程的样本函数在每个时间点 t 处都可以是一个复数。
复随机过程的理论涉及到复数域上的概率空间和概率测度。与实随机过程相比,复随机过程在信号处理、通信系统、量子力学等领域中具有重要的应用,因为它们能够更灵活地表示和处理具有复数值的随机信号和随机过程。例如,在通信系统中,信号往往是复数值的,因此复随机过程的理论更适合用来建模和分析这类信号的统计特性。

总结
随机过程是描述随机现象随时间变化的数学模型。简而言之,它是一组随机变量的集合,这些随机变量的取值取决于某种随机规律,并且通常是关于时间的函数。随机过程是概率论和统计学中的重要概念,被广泛应用于模拟、风险分析、信号处理、金融工程等领域。