二叉树
一个二叉树是一个有穷的结点集合。
它是由根节点和称为其左子树和右子树的两个不相交的二叉树组成的。
二叉树可具有以下5种形态。
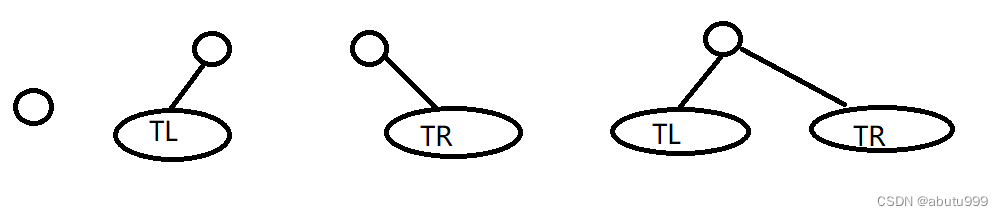
性质
- 一个二叉树第i层的最大结点数为 2 i − 1 2^{i-1} 2i−1, i ≥ 1 i \geq 1 i≥1
每层最大结点可以对应完美二叉树(满二叉树),其所有分支结点都存在左右子树,并且所有叶结点都在同一层上。
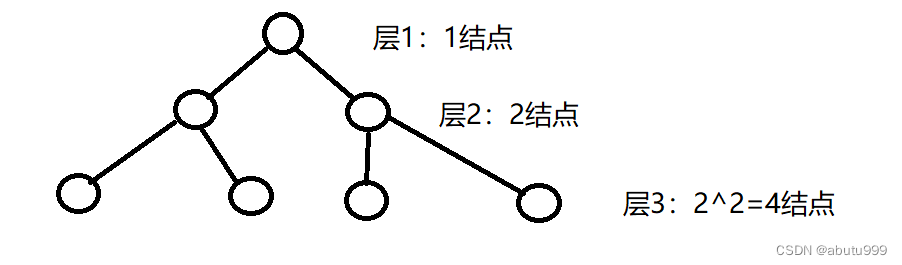
- 深度为k的二叉树有最大结点总数: 2 k − 1 2^k-1 2k−1, k ≥ 1 k \geq 1 k≥1
1 + 2 + . . . + 2 k − 1 = 2 k − 1 1 + 2 + ... +2^{k-1} = 2^k-1 1+2+...+2k−1=2k−1 - 对任何非空的二叉树 T n T_n Tn,若 n 0 n_0 n0是叶结点的个数, n 2 n_2 n2是度为2的非叶结点的个数,则: n 0 = n 2 + 1 n_0 = n_2 +1 n0=n2+1。
一颗二叉树:总结点数 = 叶节点 + 度为1的结点 + 度为2的结点
又:总结点数 = 总边数+1
且:总边数 = 2 ∗ 2* 2∗度为2的结点 + 度为1的结点
由此得到: n 0 = n 2 + 1 n_0 = n_2 +1 n0=n2+1 - 具有n个结点的完全二叉树的深度k为 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2{n} \rfloor +1 ⌊log2n⌋+1
(1) 满二叉树时:
k深度: 结点 2 k − 1 2^k-1 2k−1
n = 2 k − 1 n = 2^k-1 n=2k−1 得 k = l o g 2 n + 1 k = log_2{n+1} k=log2n+1
(2)最底层只有一个结点
k深度: 结点 2 k − 1 2^{k-1} 2k−1
解得: k = l o g 2 n + 1 k = log_2{n} +1 k=log2n+1
即 l o g 2 ( n + 1 ) ≤ k ≤ l o g 2 n + 1 log_2{(n+1)} \leq k \leq log_2n +1 log2(n+1)≤k≤log2n+1
则具有n个结点的完全二叉树的深度k为 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2{n} \rfloor +1 ⌊log2n⌋+1
存储结构
顺序存储
这种结构是川一组连续的存储单元(比如数组)存储二叉树结点的数据,结点的父子系是通过它们相对位置来反映的,而不需要任何附加的存储单元来存放指针,通常情况下顺序存储结构用于完全二叉树
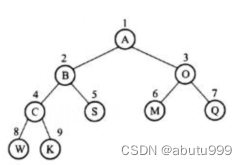
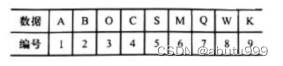
具体实现是从树的根结点开始,从上层至下层,每层从左到右,依次给结点编号并将数据存放到一个数组的对应单元中。
结点C的父结点是结点B,它的左孩子是结点w,右孩子是结点K。C结点存储单元的下标是4,将其除以2得到它的父结点B的存储单元下标,而将其乘以2则是它的左孩子w存储单元的下标,当然将其乘2再加1则是它右孩子K的存储单元下标。
链式存储
虽然顺序存储的空间利用率高,计算简单,但是其不适于一般的二叉树
如图为给定的二叉树。给出了从上至下、从左至右的层序存储的对应结点编号,其中灰色结点是为了满足顺序存储要求而增加的“虚”结点,可以在相应的存储单元存放一个特殊的数值,以区别于其他“实结点”。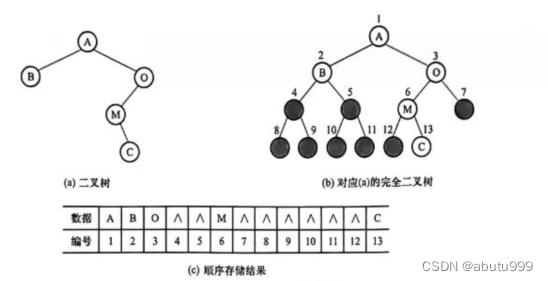
可以看到,5个结点的二叉树,顺序存储需要13个存储单元,超过一半的存储空间浪费掉了。更有甚者,对一个深度为h的右斜二叉树来讲,需要2-1个存储单元,而实际上该斜二叉树只有k个结点。
另外,二叉树的顺序存储方式避免不了顺序存储的固有缺点,即不易实现增加、删除操作。因此,二叉树的顺序存储方式适用于一定的条件,对于不需要修改的完全二叉树,是一种较好的选择。
实际上,二叉树的最常用表示方法是用链表表示,每个结点由数据和左右指针三个数据成员组成。
结构定义
typedef int ElementType;
typedef struct TNode* Position;
typedef Position BinTree;
struct TNode {ElementType Data;//结点数据BinTree Left; //指向左子树BinTree Right; //指向右子树
};操作实现
遍历
我们用L,V,R分别表示遍历左分支L,访问结点V,遍历右分支R,那么可以有以下6种情况:LVR,LRV,VLR,VRL,RLV,RVL。
规定:访问左分支在右分支之前,只剩下:LVR, LRV, VLR。
我们按照V的位置分别将其命名为:中序遍历,后序遍历,先序遍历
中序遍历
对树的任一结点的访问是在先遍历完其左子树后进行的,访问此结点后,在对其右子树遍历
遇到每个结点,其遍历过程
- 中序遍历左子树
- 访问根节点
- 中序遍历右节点
void InorderTraveral(BinTree BT) {if (BT) {InorderTraveral(BT->Left);printf("%d\n, BT->Data");InorderTraveral(BT->Right);}
}
后序遍历
对结点的左右子树先进行遍历,然后才对此结点访问。遍历是从根节点开始,遇到每个结点时,其遍历过程是:
- 后序遍历其左子树
- 后序遍历其右子树
- 访问根节点
void PostorderTraversal(BinTree BT) {if (BT) {PostorderTraversal(BT->Left);printf("%d\n, BT->Data");PostorderTraversal(BT->Right);}
}
先序遍历
对结点的访问是在其左、右子树遍历之前进行的。遍历是从根节点开始,遇到每个结点时,其遍历过程是:
- 访问根结点
- 先序遍历其左子树
- 先序遍历其右子树
void PreorderTraversal(BinTree BT) {if (BT) {printf("%d\n, BT->Data");PreorderTraversal(BT->Left);PreorderTraversal(BT->Right);}
}非递归遍历
在沿左子树深入时,进入一个结点就将其压入堆栈。
若是先序遍历,则在入栈之前访问之;当沿左分支深入不下去时,则返回,即从堆栈中弹出前面压入的结点;
若为中序遍历,则此时访同该结点,然后从该结点的右子树继续深入;
若为后序遍历,则将此结点二次入栈,然后从该结点的右子树继续深入,与前面类同,仍为进入一个结点入栈一个结点,深入不下去再返回,直到第二次从栈里弹出该结点,才访问之。
对于非递归中序遍历,遇到一个节点就将其压栈,并去遍历其左子树;当左子树结束后,从栈顶弹出结点并访问它,然后按其右指针再去中序遍历该节点的右子树。
void InorderTraversalUn(BinTree BT) {BinTree T;Stack S = CreateStack(100);T = BT;while (T || !IsEmpty(S)) {while (T) {Push(S, T);T = T->Left;}T = Pop(S);printf("%d\n, T->Data");T = T->Right;}}
层序遍历
层序遍历是按照树的层次,从第一层的根结点开始向下逐层访问每个结点,对每一层的结点按照从左到右的顺序访问。
可以设置一个队列结构,遍历从根节点开始,首先将根节指针入队,然后执行以下操作:
- 从队列取出一个元素
- 访问该元素所指向的结点
- 若元素所指向的结点的左右孩子非空,将其左、右孩子的指针入队。
不断执行这三步,直到队列为空。
void LevelorderTraversal(BinTree BT) {Queue Q;BinTree T;T = BT;Q = CreateQueue(100);AddQ(Q, T);while (!IsEmptyQ(Q)) {T = DeleteQ(Q);printf("%d\n, T->Data");if (!T->Left) { AddQ(Q, T->Left); }if (!T->Right) { AddQ(Q, T->Right); }}
}