上一篇博客我们对树有了初步了解与学习，这篇我将初步学习二叉树！！（新年快乐！）

目录

二叉树  

1、定义：

2、特点：

3、基本形态：

4、二叉树的种类：

（1）满二叉树

（2）完全二叉树 （效率高）

（3）斜树

5、二叉树的性质：

 6、二叉树的存储：

---

二叉树  

1、定义：

二叉树是每个节点最多有两个子树的树结构。二叉树是n（n>=0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

2、特点：

（1）每个结点最多有两棵子树（二叉树不存咋大于2的结点）。

（2）二叉树的子树有左右顺序之分，其子树的次序不能颠倒。

（3）即使树中的某结点只有一棵子树，也要区分它是左子树还是右子树。

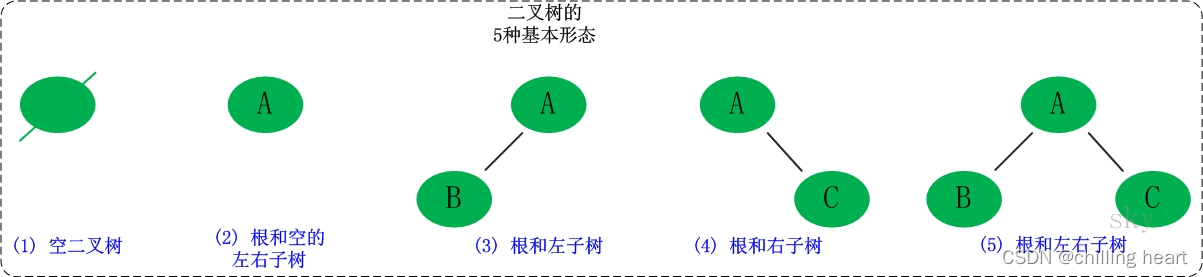
3、基本形态：

（1）空二叉树；

（2）只有一个根结点；

（3）根结点只有左子树；

（4）根结点只有右子树；

（5）根结点既有左子树又有右子树。

4、二叉树的种类：

（1）满二叉树

定义：一个二叉树每个层的结点数都达到了最大值。

【即如果一个二叉树的层数为n，则结点总数是（2^k）-1】

满二叉树是一种特殊的完全二叉树！！

特点：

a.叶子只能出现在最下一层。出现在其他层就不可能达到平衡。

b.非叶子结点的度一定为2。

c.在同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

（2）完全二叉树 （效率高）

定义：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

​

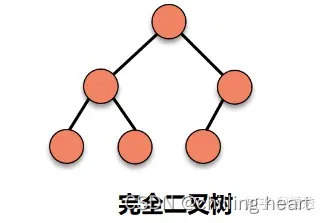
特点：

a.叶子结点只能出现在最下两层。

b.最下层的叶子一定集中在左部连续位置。

c.倒数第二层，如果有叶子结点，一定都在右部连续位置。

d.如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况。

e.同样结点数的二叉树，完全二叉树的深度最小。

（3）斜树

向哪边斜就叫啥斜树！！

左斜树：所有的结点都只有左子树的二叉树。

右斜树：所有的结点都只有右子树的二叉树。

5、二叉树的性质：

（1）

若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)  (i>0)个结点。

（2）

若规定只有根结点的二叉树的深度为1，则深度为k的二叉树的最大结点数是2^k-1 (k>=1)。

（3）

对任何一棵二叉树，如果其叶结点个数为n0，度为2的非叶结点个数为n2，则有n0=n2+1。

（4）

具有n个结点的完全二叉树的深度k为[log2n]+1上取整。（[x]表示不大于x的最大整数）

（5）

对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有结点从0开始编号，对于序号为i的结点有：
若i>0，双亲序号：(i-1)/2； i=0，i为根结点编号， 无双亲结点。
若2i+1<n，左孩子序号：2i+1，否则无左孩子。
若2i+2<n，右孩子序号：2i+2，否则无右孩子。

 6、二叉树的存储：

二叉树的存储结构分为顺序存储和类似于链表的链式存储。

链式存储：

//孩子表示法class Node6 
{int val;     //数据域Node6 left;  //左孩子的引用，常常代表左孩子为根的整棵左子树Node6 right; //右孩子的引用，常常代表右孩子为根的整棵右子树
}//孩子双亲表示法public class Node7 {int val;      //数据域Node7 left;   //左孩子的引用，常常代表左孩子为根的整棵左子树Node7 right;  //右孩子的引用，常常代表右孩子为根的整棵右子树Node7 parent; //当前结点的根结点
}

今天的学习就到这了，下篇博客咱继续！！