题目列表

3033. 修改矩阵

3034. 匹配模式数组的子数组数目 I

3035. 回文字符串的最大数量

3036. 匹配模式数组的子数组数目 II

一、修改矩阵

简单模拟即可，代码如下

class Solution {
public:vector<vector<int>> modifiedMatrix(vector<vector<int>>& matrix) {int n=matrix.size(),m=matrix[0].size();for(int i=0;i<m;i++){int mx=0;for(int j=0;j<n;j++)mx=max(mx,matrix[j][i]);for(int j=0;j<n;j++)if(matrix[j][i]<0)matrix[j][i]=mx;}return matrix;}
};

 二、匹配模式数组的子数组数目I&II

(二、四题目相同就一起讲了，暴力的做法就不在说了)

这题说实话，也不是很难，关键在于我们要将题目中的信息就行转化，即要将nums数组转换成1/0/-1的数组，然后就是该数组与pattern数组的匹配问题，等价于字符串匹配问题，只不过将字符变成了数字，用kmp算法，代码如下

class Solution {
public:int countMatchingSubarrays(vector<int>& nums, vector<int>& pattern) {int n=nums.size();vector<int> v(n-1);for(int i=0;i<n-1;i++)v[i]=(nums[i]<nums[i+1])-(nums[i]>nums[i+1]);//利用布尔值0/1来得到1/0/-1，也可以用if语句int m=pattern.size();vector<int>next(m);for(int i=1,j=0;i<m;i++){while(j&&pattern[i]!=pattern[j])j=next[j-1];if(pattern[j]==pattern[i])j++;next[i]=j;}int ans=0;for(int i=0,j=0;i<n-1;i++){while(j&&v[i]!=pattern[j])j=next[j-1];if(v[i]==pattern[j])j++;if(j==m){ans++;j=next[j-1];}}return ans;}
};

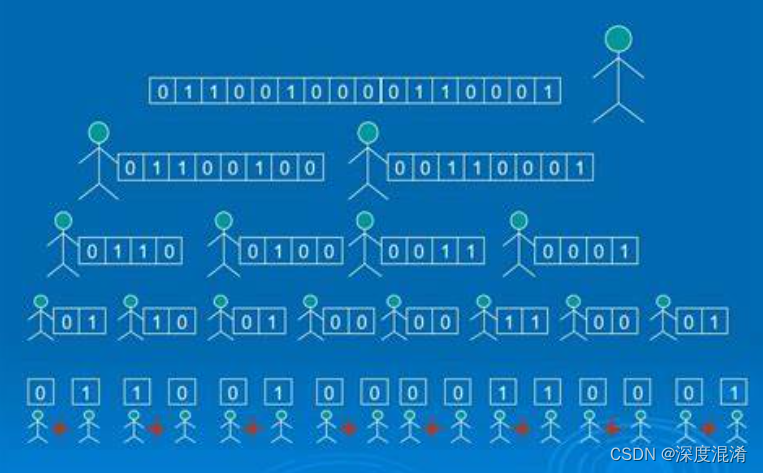
当然这题也可以用上周赛中的z函数来解答，这里既然又说到z函数，就具体讲解一下z函数的原理和操作，如下图。

那么如何用z函数这个算法来求解字符串匹配问题呢？

代码如下

class Solution {
public:int countMatchingSubarrays(vector<int>& nums, vector<int>& pattern) {int n=nums.size(),m=pattern.size(),ans=0;vector<int> v(pattern);for(int i=0;i<n-1;i++)v.push_back((nums[i]<nums[i+1])-(nums[i]>nums[i+1]));vector<int> z(v.size());z[0]=v.size();int l=0,r=0;//维护z-box的区间for(int i=1;i<v.size();i++){if(i<=r) z[i]=min(r-i+1,z[i-l]);while(i+z[i]<v.size()&&v[z[i]]==v[i+z[i]]) z[i]++;if(r<i+z[i]-1) l=i,r=i+z[i]-1;if(i>=pattern.size()&&z[i]>=pattern.size()) ans++;}return ans;}
};

三、回文字符串的最大数量

这题算是一个构造题，即如何构造回文串使得回文串的个数尽可能得多，首先我们必然要统计各个字母出现的次数，然后进行分配，从贪心的角度来思考，我们肯定是优先从字符串长度短的开始构造回文串。接下来就是如何构造回文串的问题。

对于回文串，我们只要考虑它的对称的两边是否够用即可(对于奇数长度，中间的那个我们不用考虑，因为字符的个数是足够的，大家可以细品一下这句话)，换句话说，我们可以看"成双的字符"的个数有多少，能满足多少个回文串即可，代码如下

class Solution {
public:int maxPalindromesAfterOperations(vector<string>& words) {int cnt[26]={0};int n=words.size();vector<int>v;for(auto str:words){v.push_back(str.size());for(auto e:str){cnt[e-'a']++;}}int p=0,ans=0;for(auto x:cnt) p+=x/2;//得到有几对sort(v.begin(),v.end());for(auto x:v){if(p>=x/2)ans++,p-=x/2;elsebreak;}return ans;}
};