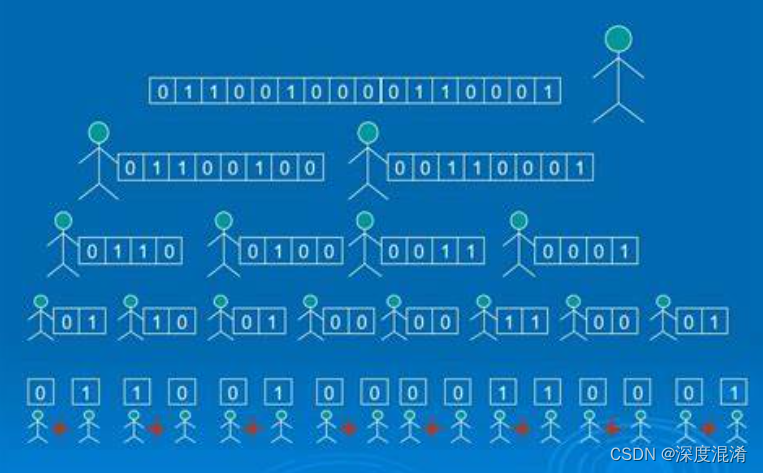
计算一个十进制数的二进制表示有多少位1？

1 遍历法（递归或非递归）

使用循环按位统计1的个数。

2 哈希查表法

利用一个数组或哈希生成一张表，存储不同二进制编码对应的值为1的二进制位数，那么在使用时，只需要去进行查询，即可在O(1)的时间复杂度内得到结果。
但是，此算法有个弊端，由于算法是采用空间换取时间的方法，当一个二进制数的位长超过一定限度时，对应的表也就会占据很大的空间，也就是说节约时间越多，花费的存储越多。另外此方法还会收到CPU缓存的限制，如果表太大，表在缓存的上下文切换也就越多，可能会导致性能没有想象中那么高。
所以，为了解决此问题，一般情况下，采用适当的二进制位长度来建表，比如8位、16位，这样情况下，可以对上述问题得到一个平衡，不仅可以享受到优越的性能，而且时间开销也没有遍历法高。

3 Variable-precision SWAR算法

在数学上，我们一般称上述问题为“计算汉明重量”，而当前一直效率最好的通用算法为variable-precision SWAR算法，该算法不仅在常数时间计算多个字节的汉明重量，而且不需要使用任何额外的内存。
 

4 源程序

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public static partial class Algorithm_Gallery{public static int Count_Setbits(int n){// initialize the resultint bitCount = 0;for (int i = 1; i <= n; i++){bitCount += Count_Setbits_Utility(i);}return bitCount;}private static int Count_Setbits_Utility(int x){if (x <= 0){return 0;}return (x % 2 == 0 ? 0 : 1) + Count_Setbits_Utility(x / 2);}public static int Count_Setbits_Second(int n){int i = 0;int ans = 0;while ((1 << i) <= n){bool k = false;int change = 1 << i;for (int j = 0; j <= n; j++){ans += (k) ? 1 : 0;if (change == 1){k = !k;change = 1 << i;}else{change--;}}i++;}return ans;}private static int Leftmost_Bit(int n){int m = 0;while (n > 1){n = n >> 1;m++;}return m;}private static int Next_Leftmost_Bit(int n, int m){int temp = 1 << m;while (n < temp){temp = temp >> 1;m--;}return m;}public static int Count_Setbits_Third(int n){int m = Leftmost_Bit(n);return Count_Setbits_Third_Utility(n, m);}public static int Count_Setbits_Third_Utility(int n, int m){if (n == 0){return 0;}m = Next_Leftmost_Bit(n, m);if (n == ((int)1 << (m + 1)) - 1){return (int)(m + 1) * (1 << m);}n = n - (1 << m);return (n + 1) + Count_Setbits_Third(n) + m * (1 << (m - 1));}}
}

POWER BY TRUFFER.CN
BY 315SOFT.COM