21中信号分解方法汇总
CEEMD(互补集合经验模态分解)CEEMDAN(自适应噪声完备集合经验模态分解)
EEMD(集合经验模态分解）EMD(经验模态分解)ESMD(极点对称模态分解）EWT(经验小波变换分解)FEEMD(快速EEMD分解)ICEEMDAN(改进自适应噪声完备集合经验模态分解)LMD(局域均值分解)MVMD(多元变分模式分解)POD(本征正交分解)REMD(固有时间尺度分解)RLMD(鲁棒性局部均值分解)SGMD(辛几何分解)SSA(奇异谱分析)SSD(奇异谱分解)SVMD(逐次变分模态分解)SWD(群分解)TVF_EMD(时变滤波器的经验模态分解)VMD(变分模态分解)WT(小波分解)

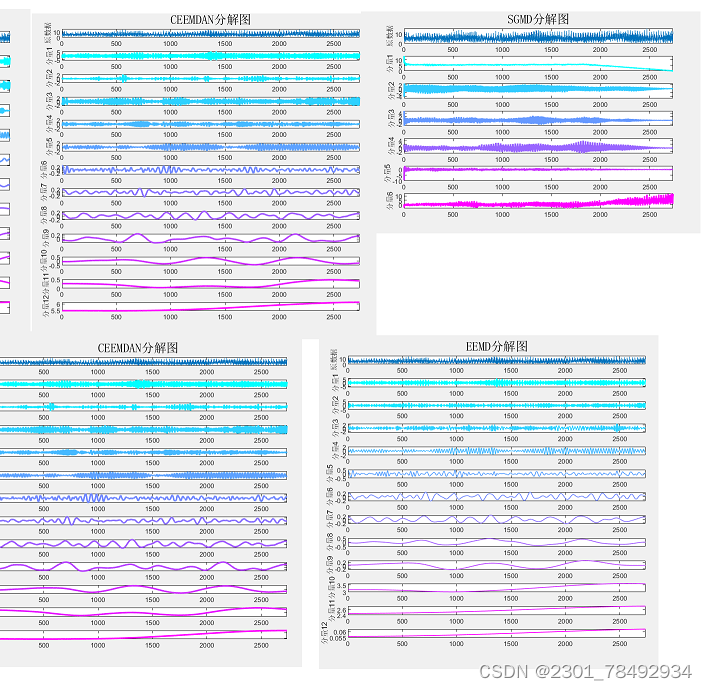
下文仅对部分分解算法效果进行展示

1. EMD (经验模态分解)

原理：EMD 是一种自适应的时频分析方法，用于将复杂信号分解为一系列固有模态函数（IMFs）。这些 IMFs 需要满足两个条件：极值点的数量和过零点的数量要么相等，要么相差最多一个；在任何时候，由局部极大值定义的上包络线和由局部极小值定义的下包络线的均值为零。EMD 通过“筛选”过程来实现分解，每次迭代都会移除信号的一个 IMF。

优点：自适应，不需要预设基函数；适用于非线性、非平稳信号。
缺点：可能受到模态混叠和端点效应的影响；对噪声敏感。

2. EEMD (集合经验模态分解)

原理：EEMD 在 EMD 的基础上添加白噪声以改善模态混叠问题。多次向原始信号中添加不同的白噪声，并对每次添加噪声后的信号进行 EMD 分解，最后对所有分解结果取平均。

优点：减少了模态混叠；提高了分解的稳定性。
缺点：需要多次分解和平均，计算量大；引入白噪声可能会影响结果的物理意义。

3. FEEMD (快速EEMD分解)

原理：FEEMD 是 EEMD 的一个优化版本，旨在提高计算效率。它采用更高效的算法来减少计算时间和内存使用。

优点：计算速度快；保留了 EEMD 的优点。
缺点：仍然需要处理与 EEMD 相同的噪声问题。

4. CEEMD (互补集合经验模态分解)

原理：CEEMD 使用成对的正负白噪声来消除 EEMD 中噪声的残余。正噪声和负噪声的效应在平均过程中相互抵消，从而减少了对结果的影响。

优点：进一步减少了噪声的影响；提高了分解的稳定性。
缺点：增加了计算复杂性；仍然需要处理噪声问题。

5. CEEMDAN (自适应噪声完备集合经验模态分解)

原理：CEEMDAN 是 CEEMD 的一个改进版本，它使用自适应噪声和更新策略来提高分解的质量和效率。在每次迭代中，它都会更新残余信号，并添加与残余信号相关的自适应噪声。

优点：通过自适应方法提高了分解的准确性；减少了噪声的影响。
缺点：可能仍然需要处理与噪声相关的问题；计算复杂。

6. ICEEMDAN (改进自适应噪声完备集合经验模态分解)

原理：ICEEMDAN 是 CEEMDAN 的一个改进版本，它进一步优化了分解算法。它可能采用更先进的噪声处理策略或改进的自适应更新机制。

优点：可能提供了更高的分解精度；减少了噪声的影响。
缺点：可能需要更多的计算资源；实现可能更复杂。

7. VMD (变分模态分解)

原理：VMD 通过约束变分问题将信号分解为一系列带宽有限的模态。它旨在找到一组模态，这些模态的总和能够最好地逼近原始信号，并且每个模态的带宽之和最小。VMD 使用了拉格朗日乘数法和交替方向乘子法（ADMM）等优化技术。

优点：提供了明确的优化目标和约束条件；适用于处理多模态信号。
缺点：计算量大；可能不适用于所有类型的信号。

8. LMD (局域均值分解)

原理：LMD 基于局部均值和局部幅值函数将信号分解为一系列乘积函数（PFs）。这些 PFs 描述了信号的局部特征，如振幅和频率调制。

优点：对局部特征敏感；适用于处理具有明显局部特征的信号。
缺点：可能不适用于所有类型的信号；实现可能较复杂。

9. RLMD (鲁棒性局部均值分解)

原理：RLMD 是 LMD 的一个改进版本，旨在提高分解的鲁棒性和稳定性。它可能采用了更先进的局部特征提取方法或噪声处理策略。

优点：提高了鲁棒性；适用于处理具有噪声或复杂特征的信号。
缺点：可能仍然受到与 LMD 相同的限制；实现可能更复杂。

10. MVMD (多元变分模式分解)

原理：MVMD 是一种用于处理多元信号或数据集的模态分解方法。它结合了 VMD 和多元统计方法，以同时处理多个信号并提取它们的共同和独特特征。

优点：适用于多元数据集；能够提取共同和独特特征。
缺点：计算量大；可能不适用于所有类型的多元信号。

11. POD (本征正交分解)

原理：POD 是一种用于提取数据集的主要特征的技术。它通过将数据投影到一组正交基上来提取主导模态。这些模态是数据集中能量最大的方向，即数据的最优正交表示。POD 通常用于流体力学、气象学等领域的数据分析。

优点：

• 提取主导特征，简化复杂系统；
• 正交基保证了模态之间的独立性；
• 适用于各种类型的数据集，包括时间序列、图像等。

缺点：

• 可能无法捕捉到数据中的非线性和非平稳特征；
• 需要足够的数据样本以确保结果的准确性；
• 对于高维数据，计算量可能很大。

12. REMD (固有时间尺度分解)

原理：REMD 是一种基于多尺度分析的方法，旨在提取信号中的固有时间尺度。它通过迭代过程逐步分解信号，以揭示其内在的时间尺度结构。REMD 通常与经验模态分解（EMD）或变分模态分解（VMD）等方法结合使用，以提供更准确的时间尺度信息。

优点：

• 适用于非线性和非平稳信号；
• 能够提取信号中的多个时间尺度；
• 对于具有不同时间尺度的复杂信号，能够提供有用的信息。

缺点：

• 计算量可能很大，特别是对于长时间序列；
• 对于某些类型的信号，可能无法准确提取所有时间尺度；
• 可能受到噪声和端点效应的影响。

13. ESMD (极点对称模态分解)

原理：ESMD 是一种基于极点对称性的信号分解方法。它通过将信号分解为一系列极点对称的模态函数来提取信号的不同特征。这些模态函数具有明确的物理意义，如频率、振幅和相位等。

优点：

• 适用于处理具有明确极点对称性的信号；
• 提取的模态函数具有明确的物理意义；
• 能够提供比传统傅里叶分析更精细的频率信息。

缺点：

• 对于非极点对称的信号，可能无法准确提取模态；
• 计算量可能较大；
• 可能受到噪声和端点效应的影响。

14. EWT (经验小波变换分解)

原理：EWT 是一种基于小波变换的信号分解方法。它通过将信号投影到一组自适应小波基上来提取信号的不同特征。这些小波基是根据信号本身的特性构建的，因此能够更好地适应信号的非平稳性和非线性。

优点：

• 适用于非平稳和非线性信号；
• 自适应小波基能够更好地匹配信号的特性；
• 能够提供比传统小波变换更精细的频率和时间分辨率。

缺点：

• 计算量可能较大；
• 对于某些类型的信号，可能无法构建合适的自适应小波基；
• 可能受到噪声和端点效应的影响。

15. SVMD (逐次变分模态分解)

原理：SVMD 是一种基于变分原理的信号分解方法。它通过构建一个变分模型来描述信号的不同模态，并通过优化算法求解该模型以提取模态。SVMD 通常结合了变分模态分解（VMD）的思想，但采用了不同的优化策略或约束条件。

优点：

• 提供了灵活的变分模型来描述信号的不同特性；
• 适用于处理多模态信号；
• 能够提供更准确的模态提取结果。

缺点：

• 计算量可能较大；
• 变分模型的构建和求解可能较复杂；
• 对于某些类型的信号，可能无法准确提取所有模态。

16. SWD (群分解)

原理：SWD 是一种基于群理论的信号分解方法。它通过将信号表示为一系列群元素的组合来提取信号的不同特征。这些群元素可以是频率、时间、空间等不同的信号属性。

优点：

• 提供了基于群理论的信号分解框架；
• 能够处理多维信号和复杂系统；
• 能够提取信号的不同属性和特征。

缺点：

• 群理论的引入可能增加了算法的复杂性；
• 对于某些类型的信号，可能无法找到合适的群结构进行分解；
• 计算量可能较大。

17. TVF_EMD (时变滤波器的经验模态分解)

原理：TVF_EMD 是经验模态分解（EMD）的一种改进版本，它引入了时变滤波器来改进模态的提取过程。时变滤波器能够适应信号的时变特性，从而更准确地提取模态。

优点：

• 提高了EMD的准确性和稳定性；
• 时变滤波器能够更好地适应信号的时变特性；
• 适用于处理非平稳和非线性信号。

缺点：

计算量可能较大，尤其是与标准EMD相比；

• 可能仍然受到噪声和端点效应的影响；
• 需要仔细选择或设计合适的时变滤波器。

18. SSA (奇异谱分析)

原理：SSA（Singular Spectrum Analysis）是一种基于矩阵分解的信号处理技术。它通过将信号表示为一个轨迹矩阵，并对该矩阵进行奇异值分解（SVD）来提取信号的不同成分。这些成分代表了信号的不同特征和时间尺度。

优点：

• 适用于非线性和非平稳信号；
• 能够提取信号的主要成分，并分离出噪声和其他干扰；
• 提供了信号的重构和预测能力。

缺点：

• 对于某些类型的信号，可能无法准确提取所有成分；
• 需要选择合适的窗口长度和嵌入维度；
• 计算量可能较大，尤其是在处理大数据集时。

19. SSD (奇异谱分解)

原理：SSD（Singular Spectrum Decomposition）是SSA的一个变种或扩展，它侧重于从数据中提取奇异谱并进行分解。SSD通常用于时间序列分析，特别是当数据中存在非线性、非平稳或周期性变化时。

优点：

• 能够揭示时间序列中的隐藏结构和周期性；
• 提供了对信号成分的解释和分离；
• 在某些情况下，比传统的频域分析更具优势。

缺点：

• 可能需要复杂的数学和计算技能来理解和实现；
• 对于某些类型的信号，可能不是最佳的分析工具；
• 计算量和数据需求可能较大。

20. WT (小波分解)

原理：WT（Wavelet Transform）是一种多分辨率分析方法，它通过将信号表示为一系列小波函数的线性组合来提取信号的不同特征。小波分解提供了在时间和频率上同时局部化的分析，因此特别适用于处理非平稳信号。

优点：

• 提供了时间和频率的局部化分析；
• 适用于处理非平稳和非线性信号；
• 提供了多分辨率分解的能力。

缺点：

• 小波基的选择可能影响分析结果；
• 对于某些类型的信号，可能不是最优的分析工具；
• 计算量可能较大，尤其是在处理大数据集时。

每种方法都有其独特的优点和局限性，选择哪种方法取决于特定应用的需求和信号的特性。在实际应用中，可能需要结合多种方法来获得最佳的分析结果。