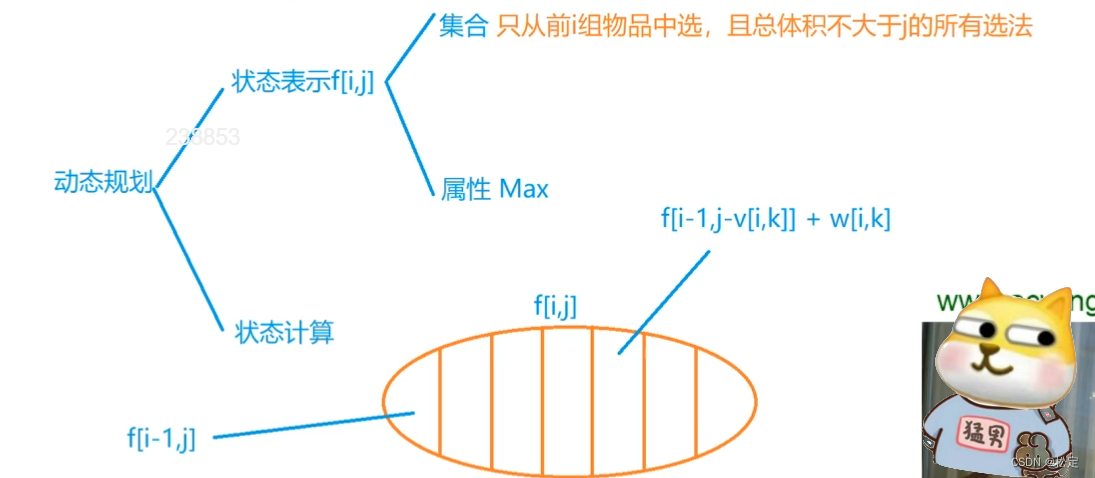
杨氏矩阵
有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,请编写程序在这样的矩阵中查找某个数字是否存在。
要求:时间复杂度小于O(N);
分析
若要满足要求时间复杂度小于O(N),就不能每一行一个个找。
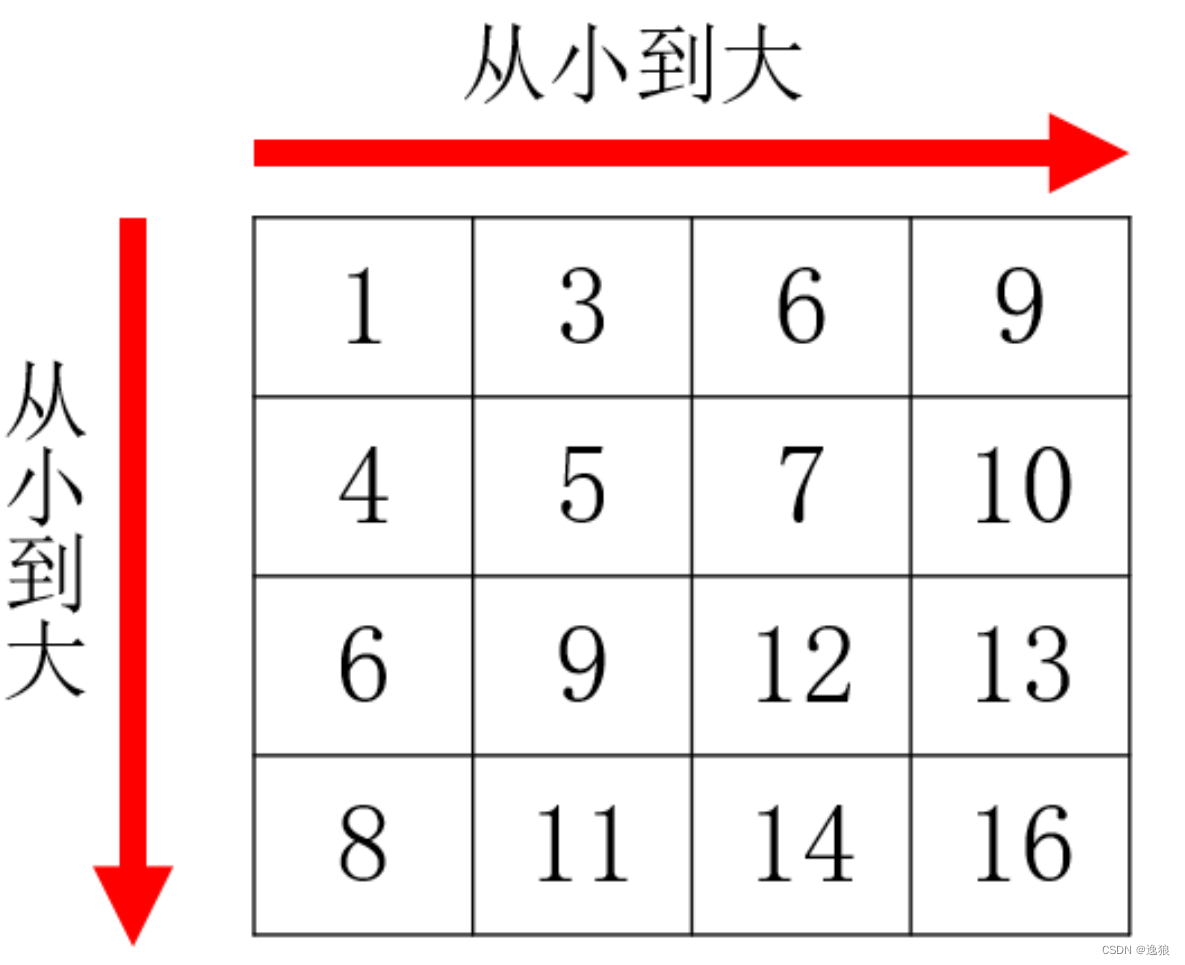
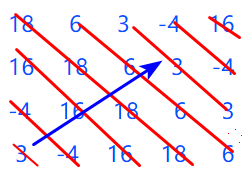
根据杨氏矩阵的特点(行递增、列递增),我们可以从矩阵的右上角开始,
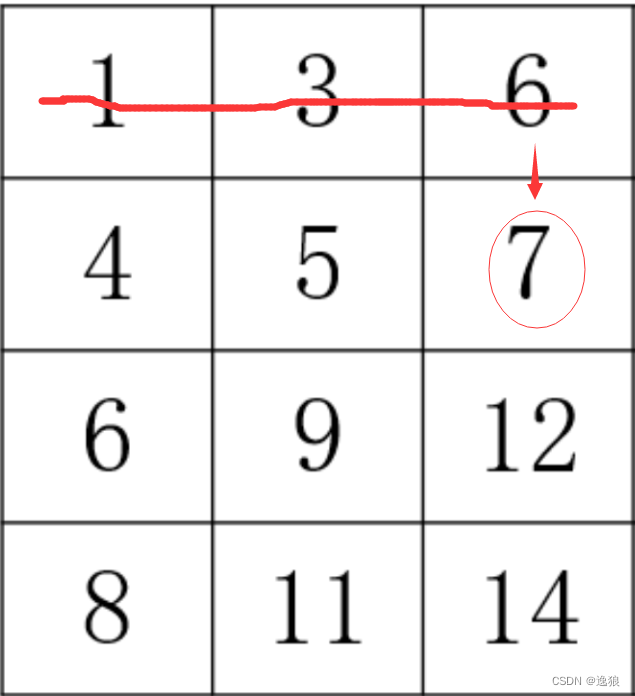
就比如我们要找上图中的数字7,
9>7,因为列递增 ,9是该列最小的数字,都大于7,所以第4列的数字都比7大,排除第4列
右上角数字变为了6,6<7,因为行递增,6是该行最大的数字,都小于7,所以第1行的数字都比7小,排除第1行

右上角数字变为了7,7=7,找到了
代码实现
// 假设有4列,x行,y列,key是要找的数字
int FindNum(int arr[][4], int x, int y, int key)
{int i = 0;int j = y - 1;//满足此循环,i和j都是合法的while (j >= 0 && i < x){if (arr[i][j] > key){j--;}else if (arr[i][j] < key){i++;}else{return 1;//找到了}}return 0;//没找到
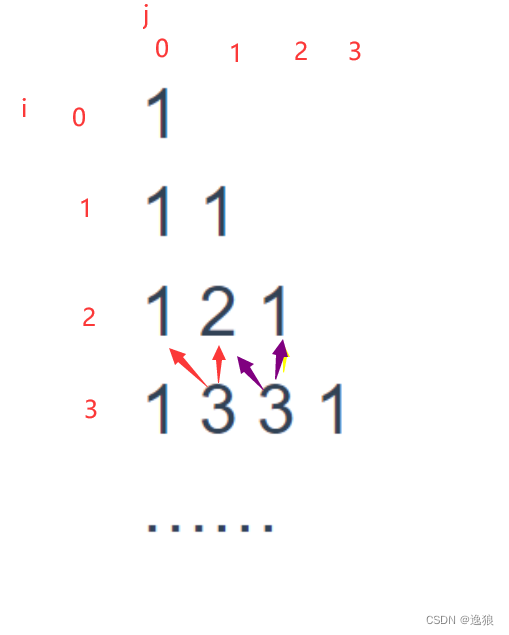
}杨辉三角
在屏幕上打印杨辉三角
分析
杨辉三角的特点:除了外围的数字为1,其他满足 数字 = 这列的上一行数字 + 上一行前一列数字
我们定义有i行j列

其中数字是1的下标满足:j==0或i==j
其他数字的下标满足:[i][j] = [i-1][j] + [i-1][j-1]
代码实现
#include<stdio.h>
//在屏幕上打印杨辉三角。
void YanghuiTriangle(int arr[][4], int n)
{for (int i = 0; i < n; i++){for (int j = 0; j <= i; j++){if (j == 0 || i == j){arr[i][j] = 1;}else{arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];}}}//打印for (int i = 0; i < n; i++){for (int j = 0; j <= i; j++){printf("%d ", arr[i][j]);}printf("\n");}
}
int main()
{int arr[4][4] = { 0 };YanghuiTriangle(arr, 4);return 0;
}