强化学习（GPS）

GPS——Guided Policy Search引导策略搜索

GPS目前被作为基础算法广泛应用于各种强化学习任务中，其出发点在于纯粹的策略梯度方法在更新参数时不会用到环境模型因而属于一种无模型强化学习算法。由于没有利用任何环境的内在属性，使得其训练只能完全依靠试错，效率较低。

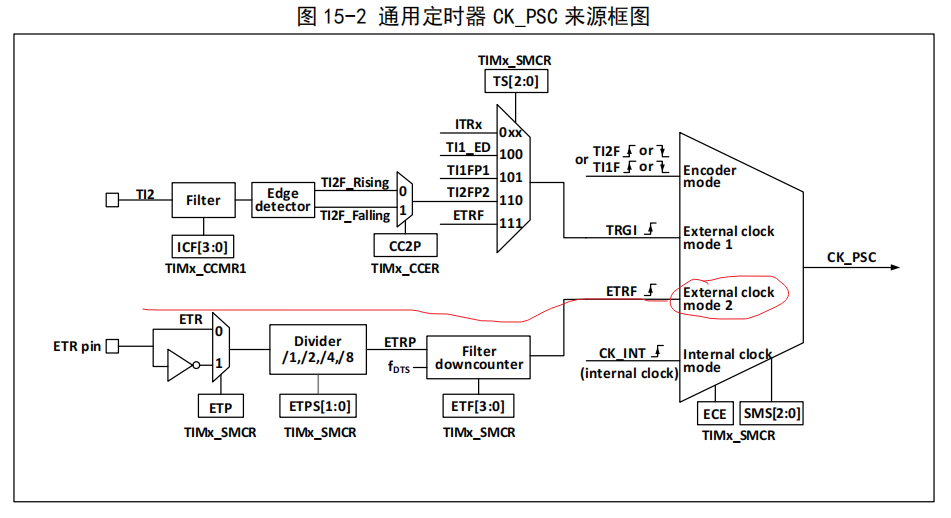
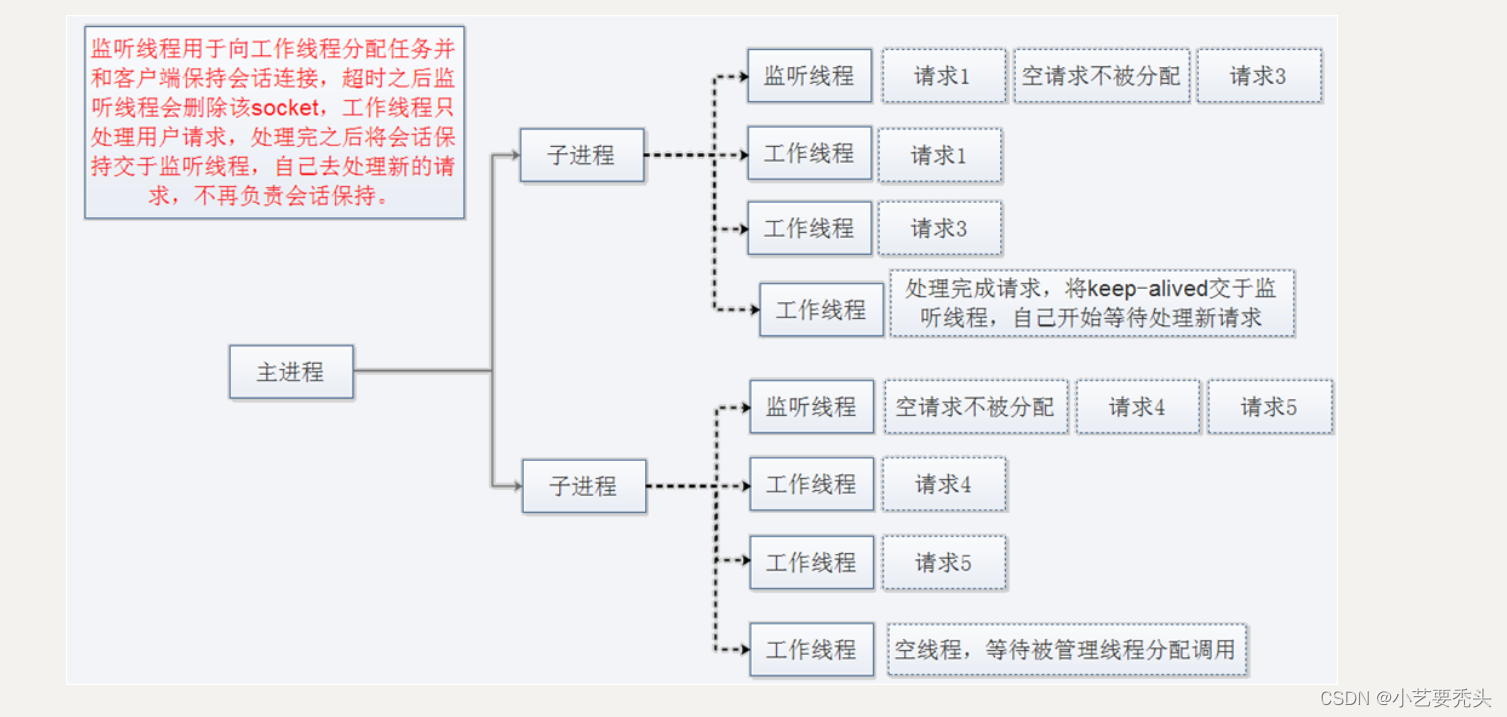
开环方法：开放循环控制或非反馈控制，是一种控制策略，其中系统的输出或行为仅依赖于预设的指令或计划，而不考虑实际输出或环境状态的变化。在开环控制中，一旦确定了控制策略，就会一直执行下去，不会根据系统的实际表现进行调整。

闭环方法：反馈控制，涉及到系统通过传感器持续监测器输出或环境状态，并将这些信息反馈到控制系统中，以调整其输入或行为。闭环控制能够自动纠正偏差，因此对环境变化和不确定性有更好的适应性。

路径优化算法是一个开环方法，策略梯度是一个闭环方法，将两者相结合，利用路径优化算法的输出结果来指导策略梯度方法的训练过程，从而提高策略梯方法的效率，即GPS算法。

GPS-v1

基本思想：首先使用路径优化算法产生一些训练数据并加入训练集中用以指导后续策略梯度方法的训练。但是策略梯度方法是在线策略算法，只能使用当前策略采样得到的数据来估计梯度从而更新参数，为了能够使用其他策略采样的数据，这里必须要使用一种技术：重要性采样。

重要性采样（一种用于估计概率分布或函数期望值的方法）：

基本思想：如果想要估计某个函数 $f\left ( x \right )$ 在概率分布 $P\left ( x \right )$ 下的期望值 $E_{P}\left [ f\left ( x \right ) \right ]$ ，可以利用一个与 $P\left ( x \right )$ 相关但更易于采样的分布 $Q\left ( x \right )$ ，来近似这个期望值。

从 $Q\left ( x \right )$ 中抽取样本 $x_{i}$ ，并为每个样本 $x_{i}$ 加上一个权重 $w\left ( x_{i} \right )$ ，这个权重是 $P\left ( x_{i} \right )$ 与 $Q\left ( x _{i}\right )$ 的比值。

基于重要性采样的策略梯度方法

在其他策略采样处的样本分布的基础上进行新策略的搜索，一旦新策略的样本分布与采样样本分布相距较远时，无法保证估计梯度的准确性。前面有工作是通过计算重要性权重的方差来判断新策略的准确性的，但是对于很长的路径，重要性权重在大部分地方都为0，方差也很小，但是并不能说明什么问题，V1版本的GPS算法通过在优化目标上额外加入重要性权重的对数值的方法，来“软最大化”重要性权重值，毕竟重要性权重越大，代表新策略分布与采样分布更为接近。

伪代码

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/260965.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！