前言

虽然我不应该再看NeRF相关的东西了，但是我还是觉得这个论文的题目很有意思，毕竟我认为神经网络本来就是模拟生物大脑的一个模型，那么我们应该更多的注意一些生物的机制，这些机制如果能得以很好的建模，或许能为神经网络结构下一步的开发提供思路。

简介

不同于NeRF依赖神经网络的权重来存储三维信息，BioNeRF利用感知启发的方式来融合多种输入，来改进模型中的记忆模块。并且该模型模拟了视锥细胞的功能，使其专注于纹理信息的提取。因此在这个意义上，记忆模块实际上是对形状信息和纹理信息进行组合。

论文链接
GitHub

（ps.感觉有种水论文讲故事的感觉）

NeRF介绍

$$\begin{gathered} (R,G,B,\Delta )=F_{\theta }(x,y,z,\theta ,\varphi ) \\ c(x,y,z,\theta ,\varphi )=\int (R,G,B{)}_i{\Delta }_{i}di \end{gathered}$$
NeRF本质上是利用一个MLP，来对一个五元组输入，输出一个四位输出，包含当前点的RGB三色，以及其密度$\Delta$。因此可以认为，物体的三维信息实际上保存在模型参数中。这也极大的节省了内存，是一种高效利用内存的技术。

NeRF其中一个关键概念是，它将复杂的真实世界的三维表示编码为神经网络的参数。此外，该模型将体积密度预测限制为相机位置的函数，从而允许RGB颜色预测为位置和观看方向的函数。这些概念类似于受神经科学发现和锥体细胞原理启发的一些生物学上更合理的研究，特别是关于引导信息流的环境和整合记忆的想法，负责根据过去的经验提供额外的环境。

BioNeRF

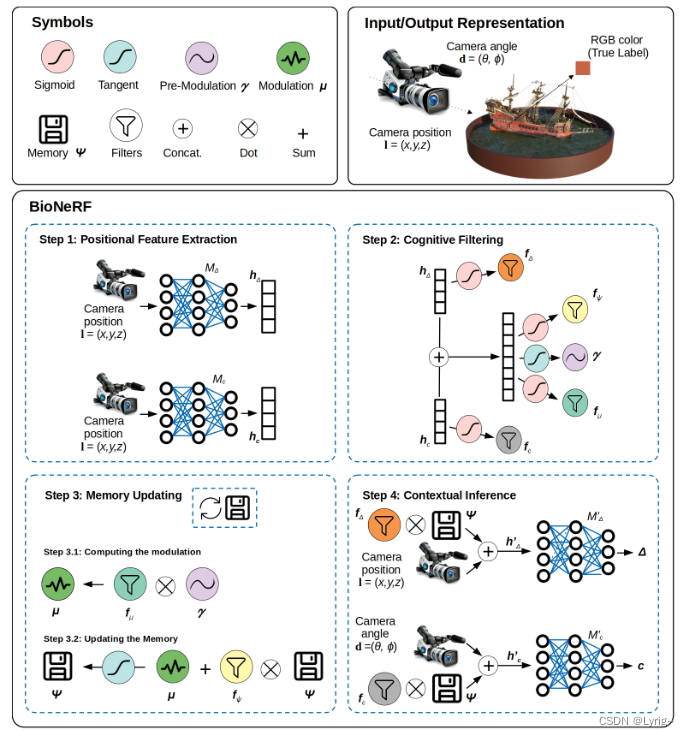
位置编码提取

第一步，将图像输入同时输入两个独立的神经网络$M_{\Delta },M_c$，两者的结构虽然相同，但是并不共享参数。

感知过滤

ps . 我们称这些为过滤的主要原始是，他会将输入特征映射到[0,1]区间。
这一阶段主要是针对上一阶段得到的特征编码进行进一步计算，有四种过滤方式:密度$f_{\Delta }$、颜色$f_c$、记忆$f_{\Psi }$、调整（调制）$f_{\mu }$。
$$\begin{gathered} f_{\Delta }=\sigma (h_{\Delta }) \\ {f}_c=\sigma (h_c) \\ {f}_{\Psi }=\sigma (W_{\Psi }[h_{\Delta },h_c]+b_{\Psi }) \\ {f}_{\mu }=\sigma (W_{\mu }[h_{\Delta },h_c]+b_{\mu }) \end{gathered}$$
其中$\sigma$是sigmoid函数。

预调制$\gamma$满足:
$$\gamma =tanh(W_{\gamma }[h_{\Delta },h_c]+b_{\gamma })$$

记忆更新

首先需要先进行一步计算如下。·
$$\mu =f_{\mu }\otimes \gamma$$

作为新的信息，之后用下式更新记忆内容:
$$\Psi =tanh(W_{\Psi }(\mu +(f_{\Psi }\otimes \Psi ))+b_{\Psi })$$

纹理推断

利用前文更新的记忆以及得到的结果，还有相机位姿，concat得到新的特征$h_{\Delta }^{\prime },h_c^{\prime }$:
$$\begin{gathered} h_{\Delta }^{\prime }=[\Psi \otimes f_{\Delta },I] \\ {h}_c^{\prime }=[\Psi \otimes f_c,d] \\ I=(x,y,z) \\ d=(\theta ,\varphi ) \end{gathered}$$
再利用两个独立的神经网络作为解码器，得到$c,\Delta$

损失函数

就是纯粹的损失函数。

量化验证

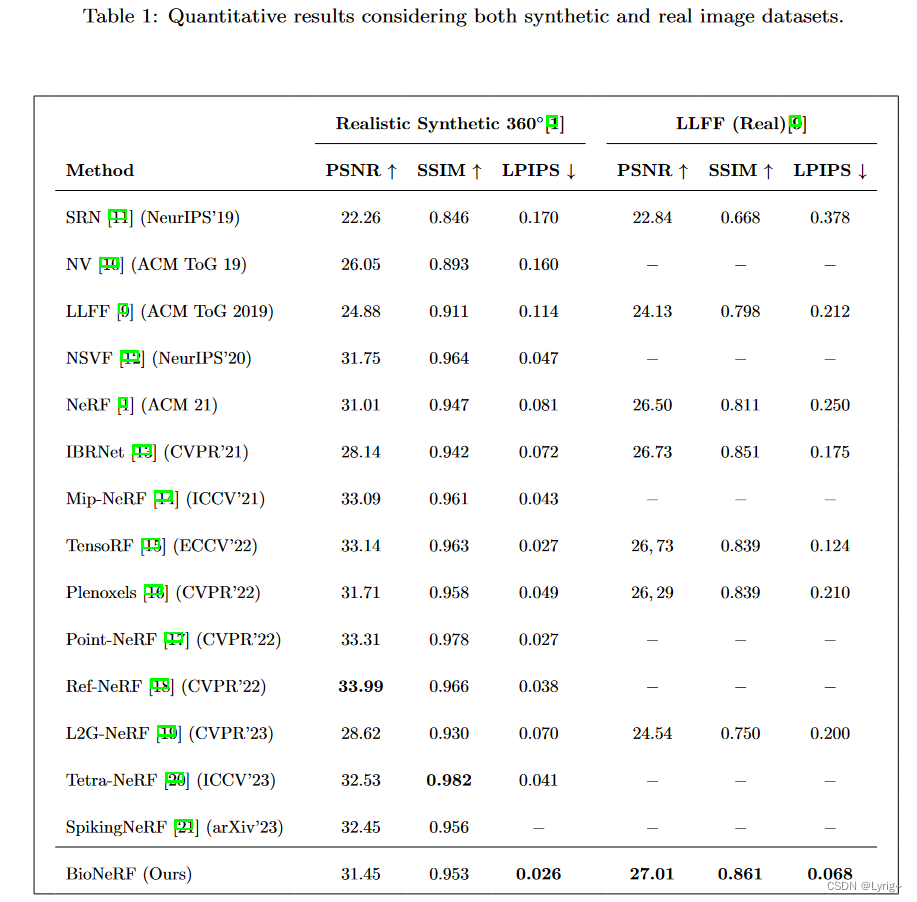
总结

感觉还是有点失望吧，这篇文章虽然说，是模仿生物视觉成像，不过依然存在以下问题：

1. 生物中的记忆力表示，能否仅仅表示为一个张量呢？这种记忆力，是否可能也是作为一个神经网络，以参数的形式进行表示呢？
2. 对比CodeNeRF，PixelNeRF等单视点成像的NeRF研究而言，改模型甚至难以单视点成像，是否说明其本身对于三维形状的提取还不如前两篇文章呢？
3. 实际上不难发现，这篇文章提到的神经网络实际上参数量很大，性能的提升，是否可能主要受到参数量的影响呢？
4. 这种记忆力机制，能否由一个Triplane来表示呢？感觉应该能起到相同的效果，甚至说，如果你认为Triplane不行，我们可以造两个Triplane，分别表示色彩和形状？如此说来这不是更复合生物特征？
5. 文中提到的记忆力更新，感觉可以类比为一种kqv的注意力机制不是吗？感觉有编故事的嫌疑。

优点：
1.提到了记忆机制，这或许为解释Triplane在NeRF中非常有效的原因，因为Triplane实际上提供了一种记忆机制。
2.结果好。