本文主要参考视频如下:
数字信号处理9-1_线性时不变系统对复指数信号的响应_哔哩哔哩_bilibili
傅里叶分析的主要研究内容如下所示:
注意,计算机中使用的离散傅里叶变换并不是离散时间傅里叶变换;
前四种都是理论上的变换方式,最后一种是计算机应用中的变换方式。
连续时间周期信号的傅里叶级数
要注意,连续时间周期信号的傅里叶级数是一个离散的结果,是一系列谐波的离散组合。
理论上,任何一个周期信号都可以进行傅里叶级数的分解,但是不一定能收敛,所以一般只有满足狄利赫里条件的周期信号才能展开成傅里叶级数。
满足狄利赫里条件时,在不连续的点处会出现吉布斯现象
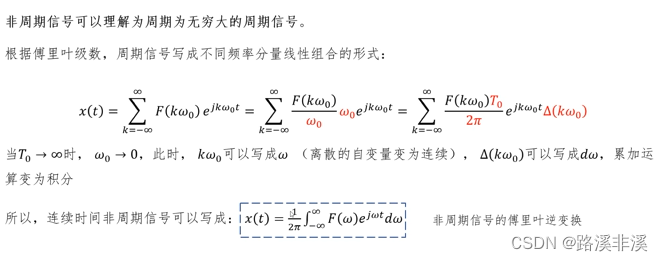
连续时间非周期信号的傅里叶变换
注意,连续时间非周期信号的傅里叶变换是一个频率密度的概念,是一个连续的函数,以w为自变量
频谱越来越密。
逆变换到时域
周期信号的傅里叶级数也可以统一到傅里叶变换
注意,傅里叶级数的结果是频谱,傅里叶变换的结果是频谱密度。
连续时间傅里叶变换的性质
1、共轭和共轭对称性
2
3
4
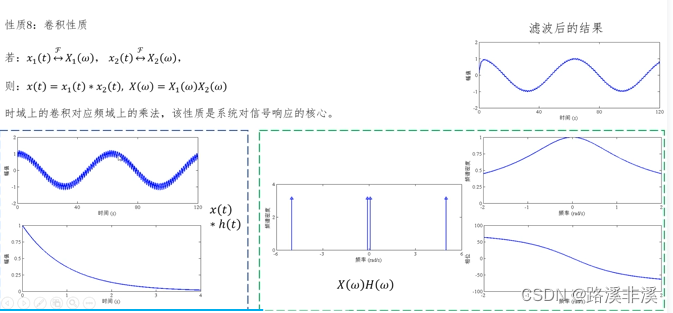
如果时域卷积不方便计算,可以转换成对应频率的相乘。
5
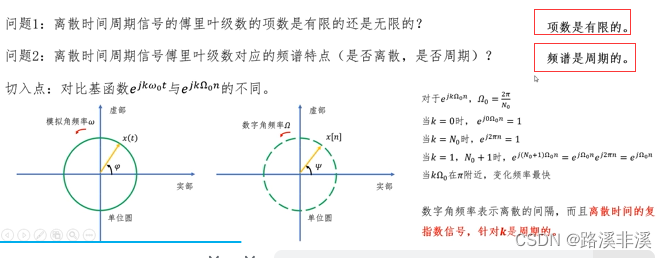
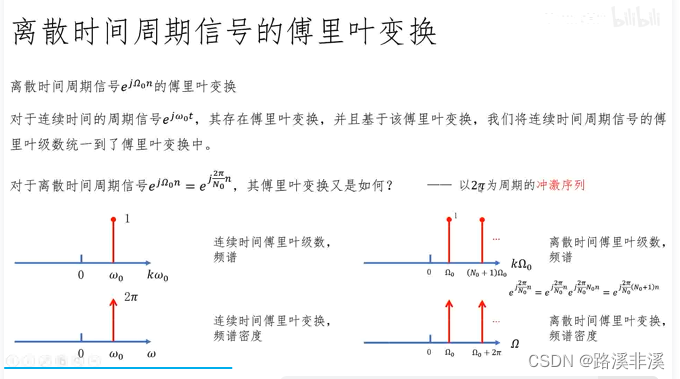
离散时间周期信号的傅里叶级数
注意下,连续时间周期信号的傅里叶级数是一个无穷级数;
离散时间周期信号的傅里叶级数只需要在一个周期上展开即可;
举个例子
离散时间周期信号的频谱是周期延拓的
存在性
可见,任何离散时间周期信号的傅里叶级数必定存在,不需要满足什么额外条件;
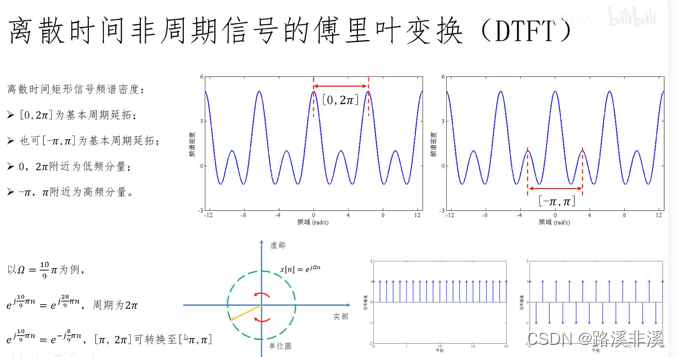
离散时间非周期信号的傅里叶变换
逆变换
存在性
频谱密度图像是以2π为周期进行周期沿拓的
离散时间周期信号也可以统一到傅里叶变换
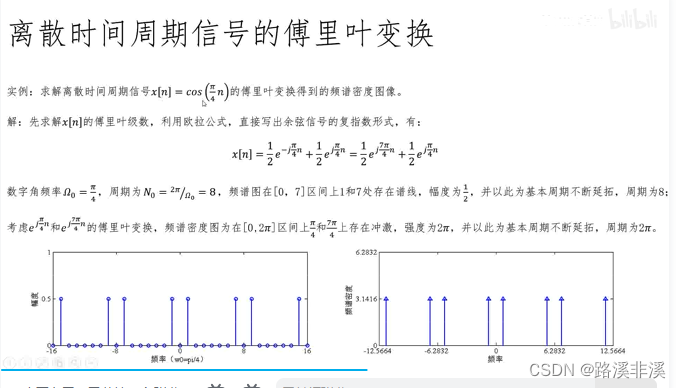
举个例子
离散时间傅里叶变换的性质
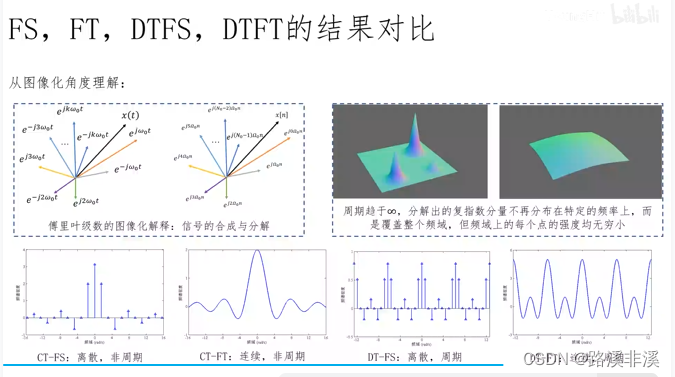
以上几种傅里叶变换的对比
图像化理解
离散傅里叶变换DFT
离散傅里叶变换是基于离散时间周期信号的傅里叶级数的,是计算机处理信号的方式。
它是暴力地将离散信号的长度N0就看做周期为N0的离散时间周期信号,然后计算其DFS,但是相比DFS会少一个系数,需要我们手动处理,这就是DFT
这种简单粗暴的方式是否合理呢?给一颗定心丸,肯定是合理的。
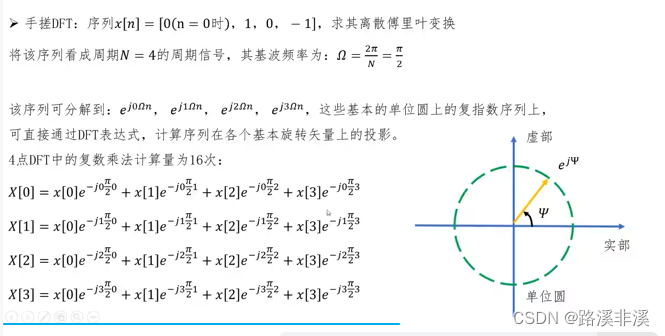
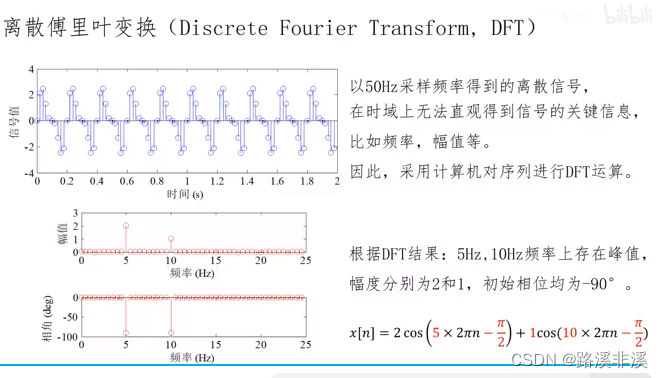
举个例子
再举个实际的例子
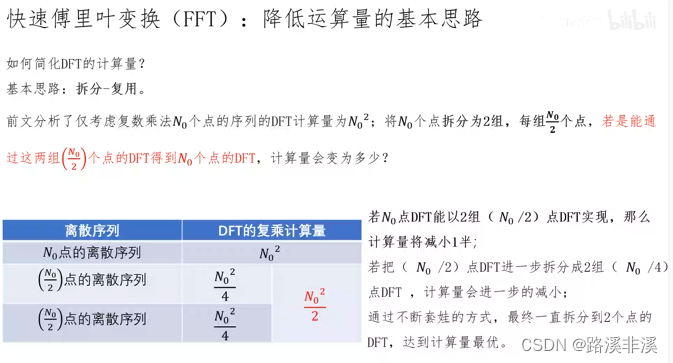
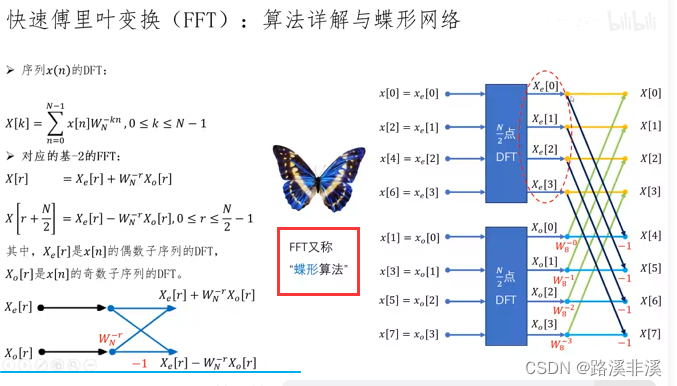
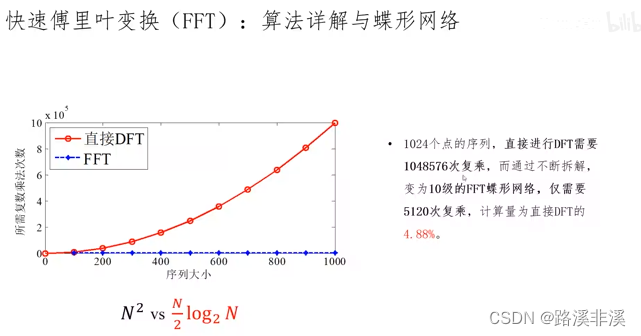
快速傅里叶变换FFT
FFT其实就是DFT的快速算法
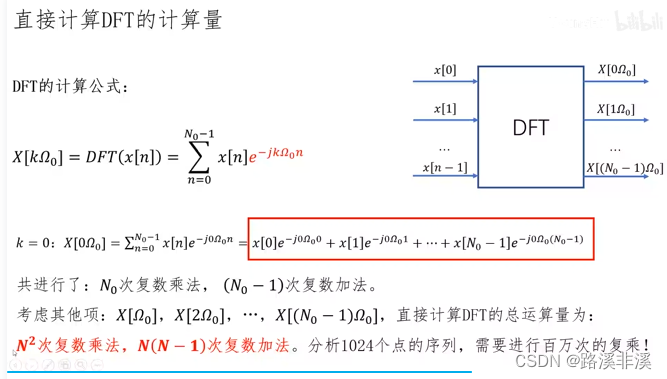
DFT的计算量
具体实现过程可参考这个视频
数字信号处理13-2_快速傅里叶变换(FFT)-降低运算量的基本思路_哔哩哔哩_bilibili
不在此赘述了
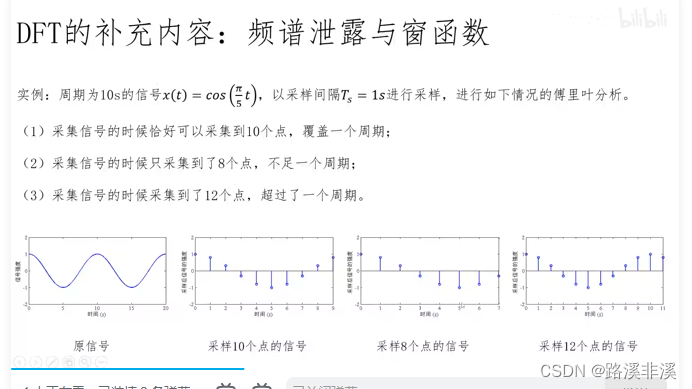
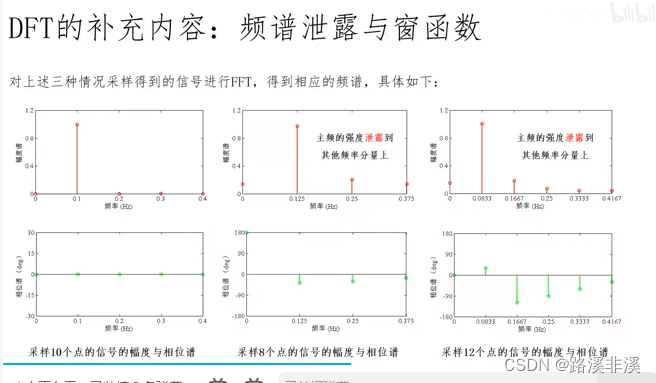
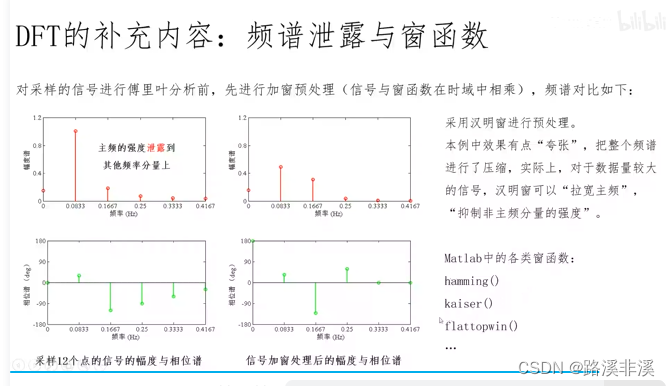
频谱泄漏和窗函数
举个实例来说明什么是频谱泄漏
假如刚好采集到一个周期,那么就能反应真实情况
但是如果信号本身就没有周期呢?或者采集的不到一个周期或者超过一个周期呢?就有误差了。
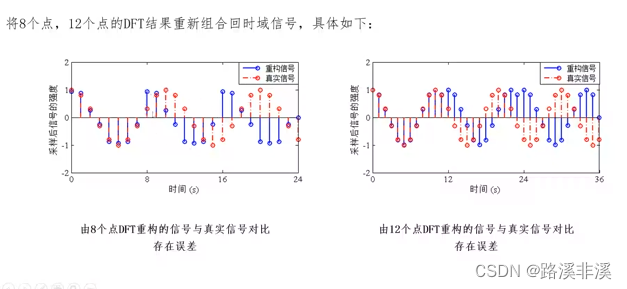
还原回去看下
如何减弱频谱泄漏的影响
实际中,窗函数一般不这么用,在滤波器设计中用得比较多。