【算法与数据结构】回溯算法、贪心算法、动态规划、图论（笔记三）

文章目录

七、回溯算法
八、贪心算法
九、动态规划
- 9.1 背包问题
- 9.2 01背包
- 9.3 完全背包
- 9.4 多重背包
十、图论
- 10.1 深度优先搜索
- 10.2 广度优先搜索
- 10.3 并查集

最近博主学习了算法与数据结构的一些视频，在这个文章做一些笔记和心得，本篇文章就写了一些基础算法和数据结构的知识点，具体题目解析会放在另外一篇文章。在学习时已经有C， C++的基础。文章附上了学习的代码，仅供大家参考。如果有问题，有错误欢迎大家留言。算法与数据结构一共有三篇文章，剩余文章可以在【CSDN文章】晚安66博客文章索引找到。

七、回溯算法

回溯算法也可以叫回溯搜索法，它是一种搜索的方式。回溯是递归的副产品，有递归就有回溯，因此回溯函数就是递归函数。回溯法的本质是穷举，穷举所有可能，然后选出我们想要的答案。如果想要令回溯法更加高效一些，那就加一些剪枝操作。虽然说回溯法并不高效，但是一些问题不得不用回溯法，能用暴力搜索解出来就不错了，在剪枝，除此之外没有更高效的解法。回溯法用来及诶觉以下的几个问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

回溯法解决的问题可以抽象为树形结构，因为回溯法解决的问题都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成树的深度。递归就要有终止条件，所以必然是一颗高度有限的树。回溯算法的伪代码：

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

八、贪心算法

贪心算法的本质是选择每一阶段的局部最优，从而达到全局最优。贪心算法经典问题有：背包问题，买卖股票的最佳时机。贪心算法没有固定的套路，说白了就是常识性推导加上举反例。贪心算法一般分为以下四个步骤：

1、将问题分解为若干个子问题
2、找出合适的贪心策略
3、求解每一个子问题的最优解
4、将局部最优解堆叠成全局最优解

九、动态规划

动态规划(Dynamic Programming, DP)，如果一个问题有很多重叠的子问题，使用动态规划是最有效的。所有动态规划总每一个状态由上一个状态推导出来，这一点就区别于贪心算法，贪心算法没有状态变量的推导，而是从局部直接选最优的。动态规划问题可以分为下面五个步骤：

1、确定dp数组(dp table)以及下标的含义
2、确定递推公式
3、dp数组如何初始化
4、确定遍历顺序
5、举例推导dp数组
在很多动态规划题目当中，确定了递推公式，题目就自然的解出来了。同时，在debug动态规划题目是，将dp数组打印出来，观察其变化是否按照自己所预想的那样。

9.1 背包问题

对于背包问题来说，主要可以分为两个部分：背包和物品。背包的最大容量为 $V$ ，物品具有价值 $W$ ，体积 $v$ 以及每个物品的数量。如果根据物品数量进行分类，可以分为01背包问题，完全背包问题，多重背包问题和分组背包问题：

01背包：每种物品的数量只有一个；
完全背包：物品数量有无数个；
多重背包：不同物品的数量可以不同；
分组背包：按组打包，每组最多选一个。
对于找工作面试来说，掌握01背包，完全背包和多重背包就够了。LeetCode的题库中没有纯01背包问题，需要转化成01背包问题。

9.2 01背包

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。题目假设如下，背包最大重量为4。

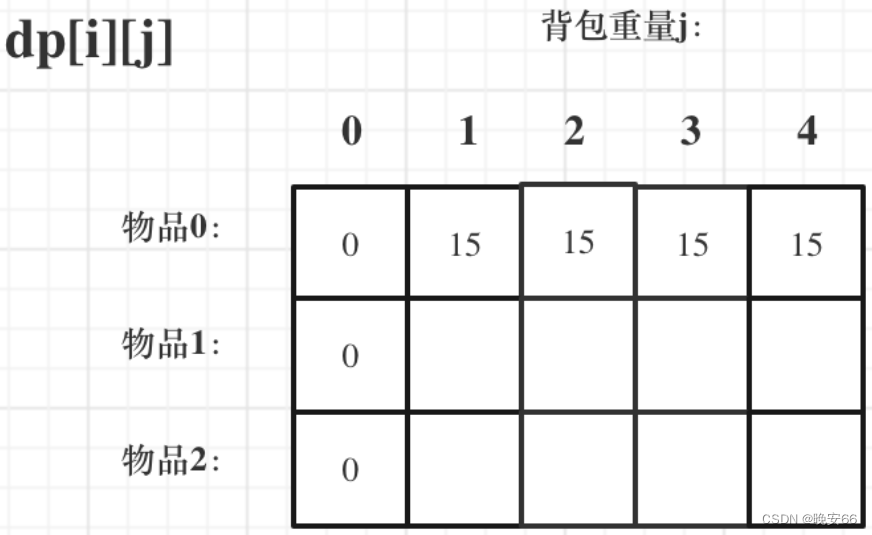
在这里插入图片描述

根据动态规划的五个步骤，我们首先确认dp数组的含义。假设一个二维 $d p [i] [j]$ 数组代表了从下标为 $[0 - i]$ 的物品里任意取，放进容量为 $j$ 的背包，最大价值总和。第二步确认递归公式。不放物品：当第 $i$ 个物品不放进去时，此时的价值和前面的相同，有 $d p [i] [j] = d p [i - 1] [j]$ 。放物品：放物品的前提是放入的物品重量不大于背包现有容量，当然这个可以用 $i f$ 语句控制。假设能放进去，那么放进去之后的价值 $d p [i] [j]$ ，可以表示为 $d p [i - 1] [j - w e i g h t [i]] + v a l u e [i]$ 。其中， $d p [i - 1] [j - w e i g h t [i]]$ 为背包容量为 $j - w e i g h t [i]$ 的时候不放物品i的最大价值， $v a l u e [i]$ 为物品 $i$ 的价值。综合以上分析，我们可以得到递归公式： $d p [i] [j] = ma x (d p [i - 1] [j], d p [i - 1] [j - w e i g h t [i]] + v a l u e [i])$ 。

第三步我们进行初始化，因为 $i$ 是由 $i - 1$ 初始化而来的，那么我们将 $d p [i] [0]$ 初始化为0。实际上我们在构建dp数组的时候可以将二维数组中的所有元素初始化为0，而非零的值将在循环遍历中被覆盖。然后初始化第一行当 $j > w e i g h t [i]$ 时（背包可以放假物品0）， $d p [0] [j]$ 应该是 $v a l u e [0]$ 。第四步，确定遍历顺序。遍历的两个维度分别是物品和背包重量，遍历物品相对比遍历背包重量更容易理解：

在这里插入图片描述

// 初始化 dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品for(int j = 0; j <= bagweight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}

当然，上述的dp数组也可以写成一维滚动数组形式。下面的代码舍去了初始化的代码，舍去下标二维dp数组的下标 $i$ 从而变成了一维数组。主要原因是 $d p [i - 1] [j]$ 完全可以用 $d p [j]$ 来表示。二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

举一个例子：物品0的重量weight[0] = 1，价值value[0] = 15。如果正序遍历dp[1] = dp[1 - weight[0]] + value[0] = 15，dp[2] = dp[2 - weight[0]] + value[0] = 30。此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。

倒序就是先算dp[2]。dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0），dp[1] = dp[1 - weight[0]] + value[0] = 15。所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。

class Solution {	// 一维dp数组（滚动数组形式）
public:int bag01(const vector<int> weight, const vector<int> value, const int bagweight) {vector<int> dp(vector<int>(bagweight + 1, 0));for (int i = 0; i < weight.size(); i++) {			// 遍历物品for (int j = bagweight; j >= weight[i]; j--) {			// 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}return dp[bagweight];}
};

简言之，一维dp数组和二维dp数组的区别在于一维的空间复杂度低，二维的更容易理解（初学者用二维即可）。以上的完整代码如下：

# include <iostream>
# include <vector>
using namespace std;class Solution {
public:int bag01(const vector<int> weight, const vector<int> value, const int bagweight) {vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));for (int j = weight[0]; j <= bagweight; j++) {		// 初始化dp[0][j] = value[0];}for (int i = 1; i < weight.size(); i++) {			// 遍历物品for (int j = 0; j <= bagweight; j++) {			// 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}return dp[weight.size() - 1][bagweight];}
};int main() {Solution s1;vector<int> weight = { 1, 3, 4 };vector<int> value = { 15, 20, 30 };int bagweight = 4;int result = s1.bag01(weight, value, bagweight);cout << result << endl;system("pause");return 0;
}

9.3 完全背包

完全背包问题可以描述为：有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。依然假设背包最大重量为4。

在这里插入图片描述

为了保证每个物品仅被添加一次，01背包内嵌的循环是从大到小遍历。而完全背包的物品是可以添加多次的，所以要从小到大去遍历。

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}

9.4 多重背包

有N种物品和一个容量为V的背包。第 $i$ 种物品最多有 $M_i$ 件可用，每件耗费的空间是 $C_i$ ，价值是 $W_i$ 。求解将哪些物品装入背包可使这些物品的耗费的空间，总和不超过背包容量，且价值总和最大。

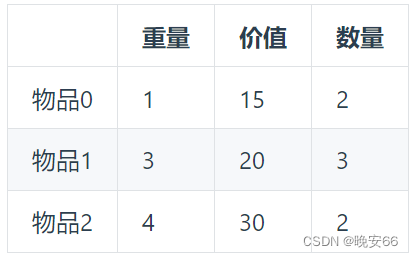
我们将物品数量摊开，其实可以将多重背包问题转换成01背包。例如：背包最大重量为10。物品的重量、价值和数量如下。那么可以转化成7个物品，每个物品只能用一次。这样就是一个01背包问题。因此我们在01背包的基础之上加上遍历个数即可。

在这里插入图片描述

#include<iostream>
#include<vector>
using namespace std;class Solution {
public:int Multip_Bag(int bagWeight, int nItem, vector<int> weight, vector<int> value, vector<int> nums) {vector<int> dp(bagWeight + 1, 0);for (int i = 0; i < nItem; i++) { // 遍历物品for (int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量// 以上为01背包，然后加一个遍历个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}return dp[bagWeight];}
};int main() {int bagWeight = 10, nItem = 3;vector<int> weight = {1, 3, 4}, value = {15, 20, 30}, nums = {2, 3, 2};Solution s1;int result = s1.Multip_Bag(bagWeight, nItem, weight, value, nums);cout << result << endl;system("pause");return 0;
}

十、图论

10.1 深度优先搜索

DFS和BFS的区别：

深度优先搜索（Depth First Search， DFS）是沿着一个方向搜索，不到黄河不死心，直到遇到绝境了，搜不下去了，再换方向（回溯）。
广度优先搜索（Breadth First Search， BFS）是先把本节点所连接的所有节点遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索的方向是四面八方的，因此被称为广度优先搜索。

因为DFS搜索就一个方向，并且需要回溯，所以用递归来实现是最方便的。二叉树遍历的递归法是DFS，而二叉树遍历的迭代法是BFS。

void dfs(参数) {处理节点dfs(图，选择的节点); // 递归回溯，撤销处理结果
}

回溯算法本质上也是一种DFS过程，DFS搜索过程可以笼统的划分为三步。一是确定输入参数；二是确定终止条件；三是处理目前搜索节点的出发路径。

void dfs(输入参数) {if (终止条件) {存放结果;return;}for (选择：本节点所连接的其他节点) {处理节点;dfs(图，选择的节点); // 递归回溯，撤销处理结果}
}

10.2 广度优先搜索

如果说深搜是一条路跑到黑然后再回溯的搜索方式，那么广搜就是一圈一圈的搜索过程。广搜的搜索方式就适合解决两个点之间最短路径的问题。因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。

10.3 并查集

并查集是当我们需要判断两个元素是否在同一个集合里的时候，我们就要想到用并查集。并查集常用来解决连通性问题。并查集有以下两个功能：

将两个元素添加到一个集合中。
判断两个元素在不在同一个集合。

设想我们将三个元素A， B，C（都是int类型）放在同一集合，其实就是将三个元素连通在一起。只需要一个一维数组来表示：father[A] = B, father[B] = C，father[C] = C。当我们使用find函数去寻找数组的元素，如果数组元素的根相同，这样就表示A与B与C连通。

// 将v，u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同，则说明在一个集合，不同两个节点相连直接返回father[v] = u;
}

find函数通过数组下标找到数组元素，一层一层寻根过程，代码如下：

// 并查集里寻根的过程
int find(int u) {if (u == father[u]) return u; // 如果根就是自己，直接返回else return find(father[u]); // 如果根不是自己，就根据数组下标一层一层向下找
}

find函数寻根的过程是通过递归的方式，不断获取father数组下标对应的数值，最终找到集合的根。而这很像在一个多叉树中，从叶子节点出发，找到根节点的过程。如果说这颗树的高度很深，每次寻根需要递归很多次。

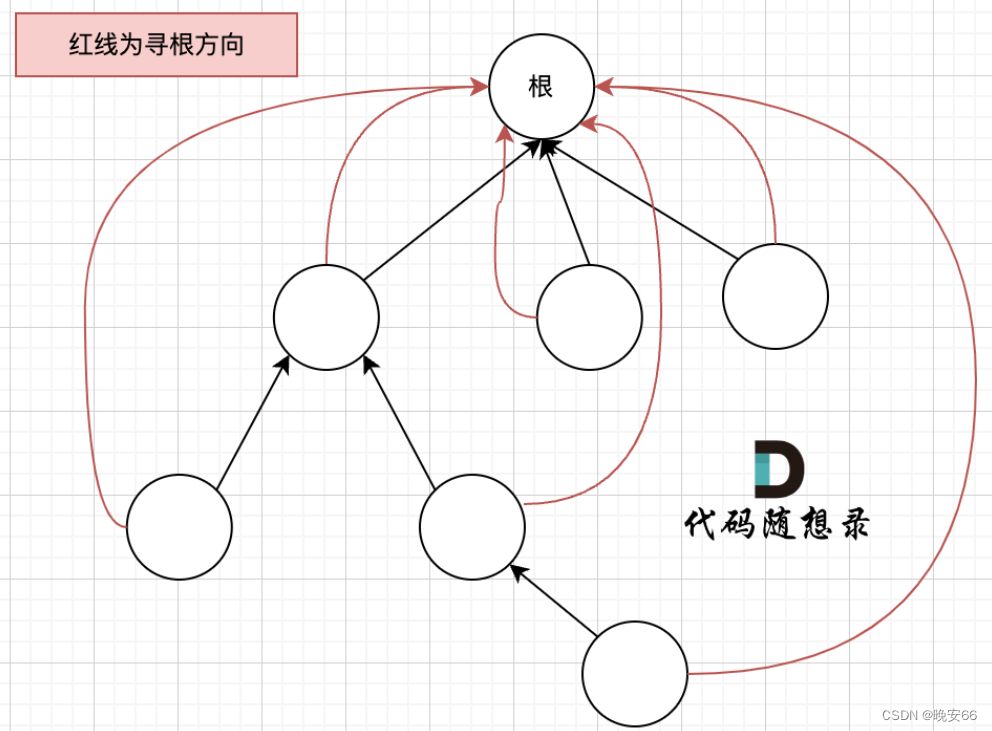
在这里插入图片描述

而我们的目的是需要知道这些节点在同一个根下就可以，因此让多茶树的叶子节点直接指向根即可，每次寻根只需要一次。

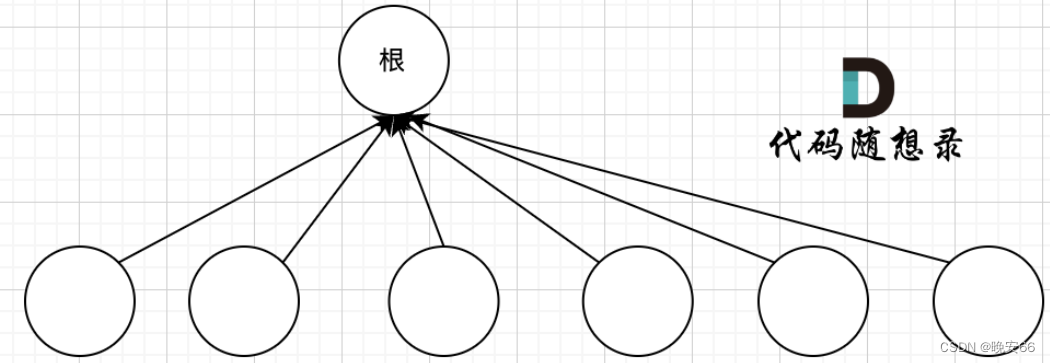
在这里插入图片描述

要实现这样的路径压缩过程，只需要在递归过程中，让father[u]接住递归函数 find(father[u])的返回结果。这样是让u的父节点直接变成find函数返回的根节点。进一步可以用三元表达式精简代码。

// 并查集里寻根的过程
int find(int u) {if (u == father[u]) return u;else return father[u] = find(father[u]); // 路径压缩
}

int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);
}

同时，father数组初始化的时候要令 father[i] = i，默认指向自己。

// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {father[i] = i;}
}

如果通过find函数找到两个元素属于同一个根的话，那么这两个元素就是同一个集合，代码如下：

// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}

结合以上加入并查集join、寻根find、初始化init和判断是否同一集合isSame函数，我们就得到一个并查集完整模板：

int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {father[i] = i;}
}
// 并查集里寻根的过程
int find(int u) {return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}// 将v->u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return ; // 如果发现根相同，则说明在一个集合，不同两个节点已经相连，直接返回father[v] = u;
}