所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

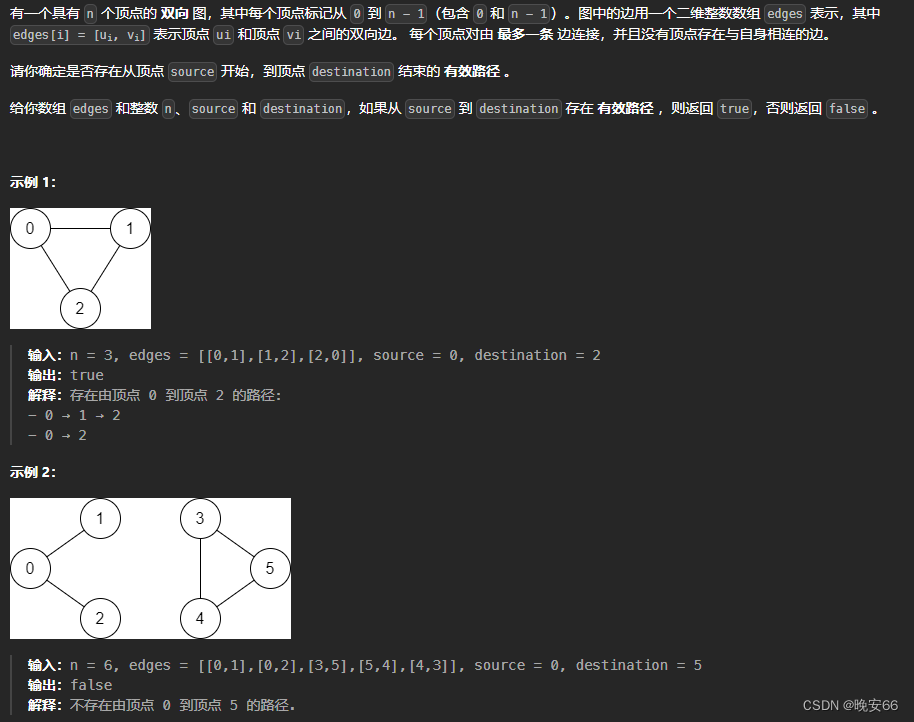
二、解法

  思路分析：本题应用并查集的理论直接就可以解决：【算法与数据结构】回溯算法、贪心算法、动态规划、图论（笔记三）。
  程序如下：

class Solution {
private:int n = 200005;		// 节点数量 200000vector<int> father = vector<int>(n, 0);	// C++里面的一种数据结构// 并查集初始化void init() {for (int i = 0; i < n; i++) {father[i] = i;}}// 并查集里寻根的过程int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);    // 路径压缩}// 判断 u 和 v是否找到同一个根bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;}// 将v->u 这条边加入并查集void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回father[v] = u;      // 根不同，则令v的父节点为u}
public:bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {init();for (int i = 0; i < edges.size(); i++) {join(edges[i][0], edges[i][1]);}return isSame(source, destination);}
};

复杂度分析：

• 时间复杂度：$O(n+m\times \alpha (m))$，其中$n$是图中的顶点数，$m$为图中边的数目（edges大小），$\alpha$是反阿克曼函数。并查集的初始化需要花费$O(n)$的时间，图中边的查询与合并的单次操作时间复杂度是$O(\alpha (m))$，主函数中一共需要$m$次。因此最终的时间复杂度为$O(n+m\times \alpha (m))$。
• 空间复杂度：$O(n)$，主要用来开辟father数组。

三、完整代码

# include <iostream>
# include <vector>
using namespace std;class Solution {
private:int n = 200005;		// 节点数量 200000vector<int> father = vector<int>(n, 0);	// C++里面的一种数据结构// 并查集初始化void init() {for (int i = 0; i < n; i++) {father[i] = i;}}// 并查集里寻根的过程int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);    // 路径压缩}// 判断 u 和 v是否找到同一个根bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;}// 将v->u 这条边加入并查集void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回father[v] = u;      // 根不同，则令v的父节点为u}
public:bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {init();for (int i = 0; i < edges.size(); i++) {join(edges[i][0], edges[i][1]);}return isSame(source, destination);}
};int main() {int n = 3, source = 0, destination = 2;vector<vector<int>> edges = { {0, 1}, {1, 2}, {2, 0} };Solution s1;bool result = s1.validPath(n, edges, source, destination);cout << result << endl;system("pause");return 0;
}

end