● 343. 整数拆分

想不到，要勇于看题解。

关键在于理解递推公式。

1、DP数组及其下标的含义：dp[i]是分解i这个数得到的最大的乘积。

2、DP数组如何初始化：dp[0]和dp[1]都没意义，所以直接不赋值，初始化dp[2]=1即可。

3、递推公式：根据题目：给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ）。可以分成两种情况：①n拆分成2个正整数的和。②n拆分成大于2个正整数的和。

①的话，dp[n]应该=j*(n-j)的最大值，②的话，dp[n]应该等于j*dp[n-j]的最大值。j是从1遍历到i-1，因为dp[n-j]是分解n-j这个数得到的最大的乘积，所以至少分解了2次，乘j就是至少分解了3次。

所以dp[n]应该取两种情况下的最大值,dp[n]=max(  j * ( n-j ), j * dp[n-j] )。这个dp[n]只是n包含j的时候分解的最大值，和前面的n包含1……j-1的时候分解的最大值没有联系起来，所以这个式子还是不对的。

因此dp[n]还要和自己比较，和之前的j对应的最大值（也就是最近一次更新的dp[n]比较），最终才是最大值。

根据公式得到从2到10的最大乘积如下：

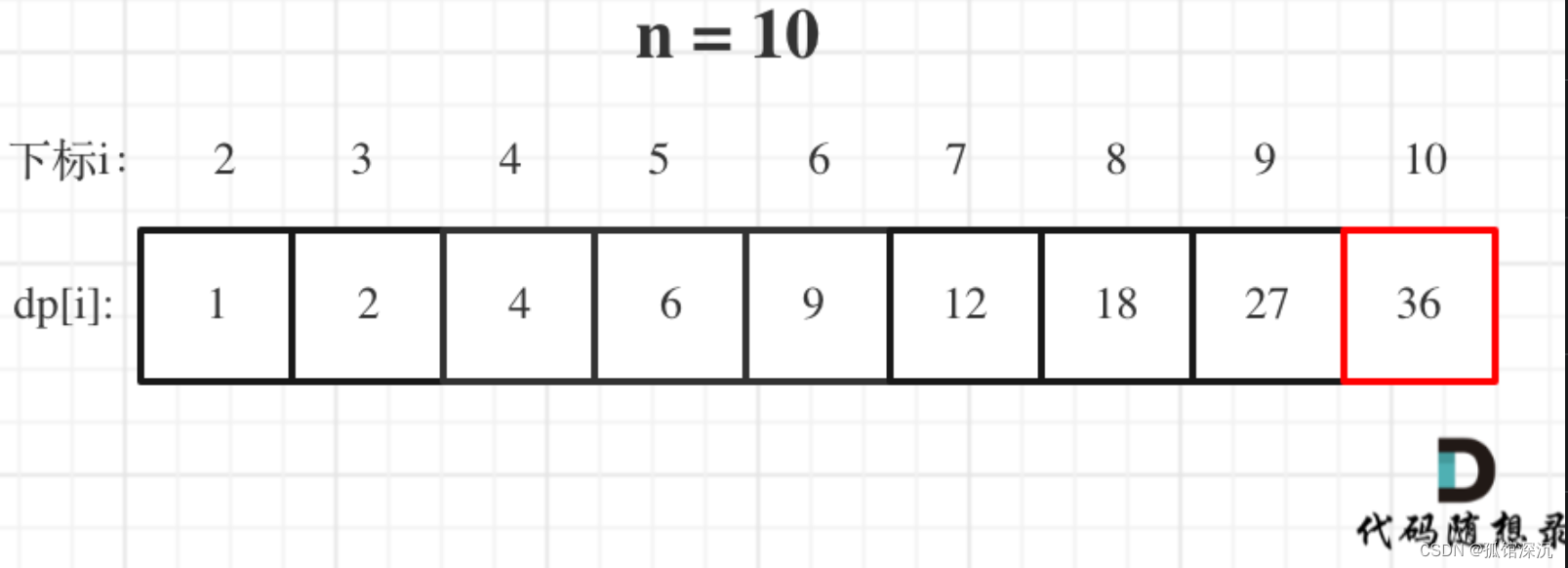
校验发现正确。

4、遍历顺序：

当然是从左到右从小到大，小的数统计好了，大的数就靠小的数的最大乘积来统计。i初始化了2，所以应该是从3到n，注意下标是对应的，最后就是返回dp[n]。对于j，一般认为从1到i-1，比如4，分解2个的话是1和3,2和2,3和1。j是1,2就统计到了所有的乘积，因为后面的是对称的，所以其实从1到i/2就行。发现分解成2个以上的话也是到i/2之前就能统计到最大值，具体原因还不知道。

5、打印DP数组。
打印如上图，发现没错。

代码：

class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1);dp[2]=1;             //初始化for(int i=3;i<=n;++i){for(int j=1;j<=i/2;++j){dp[i]=max({dp[i],j*(i-j),j*dp[i-j]});    //考虑k=2和k>2的情况，更新dp[i]}}return dp[n];}
};

● 96.不同的二叉搜索树

n=3的时候，分为以1为头结点、以2为头结点和以3为头结点三种情况。所以对于所有n，都是如此。

n=3的时候，数量是下面三个数量相加：

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量；

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量；

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量。

那么令dp[i]就是i个节点组成的二叉搜索树的数量，对于所有n，数量是下面n个数量相加：

元素1为头结点搜索树的数量=dp[n-1] * dp[0]；

……

元素n为头结点搜索树的数量 = dp[0] * dp[n-1]。

1.dp[i]含义：i个节点组成的二叉搜索树的数量

2.递推公式：

3.初始化：dp[0]=1,dp[1]=1；注意dp[0]是1，空树也是一棵搜索树。

4.遍历顺序：同样的由小推大。

代码：

class Solution {
public:int numTrees(int n) {vector<int> dp(n+1,0);dp[0]=1;//初始化for(int i=1;i<=n;++i){for(int j=0;j<i;++j){       //求和公式dp[i]+=dp[j]*dp[i-1-j]; }}return dp[n];}
};