Uncertainty-Aware Mean Teacher
- 0 FQA:
- 1 UA-MT
- 1.1 Introduction:
- 1.2 semi-supervised segmentation
- 1.3 Uncertainty-Aware Mean Teacher Framework
- 参考:
0 FQA:
Q1: 不确定感知是什么意思?不确定信息是啥?
Q2:这篇文章的精妙的点在哪?
Q3:MC dropout可以用在分类上面吗?因为原文是用在分割上面的。
Q4:mc dropout是放在哪里? 放在教师上还是学生上?为什么?
Q5: 怎么保留低不确定性,和怎么利用高不确定性的呢?
Q6: **不确定图是啥? 怎么生成的? **
A2: 概括来看,这篇文章就是改进了一下无标签的一致性损失函数。 这篇文章的精妙点在于,通过教师的mc dropout来估计每个目标预测的不确定性,在估计不确定性的指导下,计算一致性损失时过滤掉不可靠的预测,只保留可靠的预测。 让学生从教师的可靠的知识中学习,增加教师知识的可靠性。 其实就是多输出几次结果,然后取均值的感觉,然后避免网络的误差。
A3:理论上感觉是可以的,因为mc dropout 就相当于多推理几次,可能不同的点在于如何计算不确定性图。因为分割是体积,而分类是分类结果。
A4: 通过mc 让教师更加确信自己教的知识,学生也会学的更好。
A6: 其实也没有啥不确定性图,只不过是为了掩饰mc 之后出来的东西。其实就是多了一个计算熵值的步骤。有了这个map 看起来更加花里胡哨。
1 UA-MT
论文完整标题:Uncertainty-aware Self-ensembling Model for Semi-supervised 3D Left Atrium Segmentation
代码:https://github.com/yulequan/UA-MT
1.1 Introduction:
本文提出了一种新的基于不确定性的半监督学习框架(UA-MT),通过额外利用未标记的数据从3D MR图像中分割左心房。和Mean Teacher模型一样,该方法鼓励分割预测在相同输入的不同扰动下保持一致。
具体地说,本文建立了一个教师模型和一个学生模型,学生模型通过最小化标注数据上的分割监督损失和所有输入数据上的与教师模型预测输出的一致性损失进行优化。
但未标注的输入中没有提供ground truth,教师模型中的预测目标可能不可靠且有噪声。在这方面,我们设计了(UA-MT)框架,学生模型通过利用教师模型的不确定性信息,逐渐从有意义和可靠的目标中学习。除了生成目标输出,教师模型还通过Monte Carlo Dropout 估计每个目标预测的不确定性。在估计不确定性的指导下,计算一致性损失时过滤掉不可靠的预测,只保留可靠的预测(低不确定性)。因此,学生模型得到了优化,得到了更可靠的监督,并反过来鼓励教师模型生成更高质量的目标。
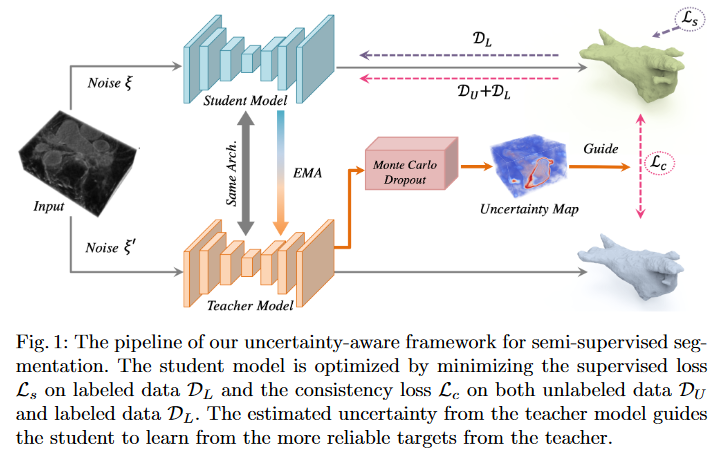
1.2 semi-supervised segmentation
半监督分割:EMA:
有监督损失,无监督一致性损失;
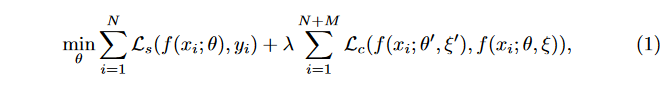
1.3 Uncertainty-Aware Mean Teacher Framework
如果没有未标记输入中的注释,教师模型的预测目标可能不可靠且有噪声。因此,我们设计了一种不确定性感知方案,使学生模型能够逐渐从更可靠的目标中学习。给定一批训练图像,教师模型不仅生成目标预测,还估计每个目标的不确定性。然后通过一致性损失来优化学生模型,该模型在估计不确定性的指导下仅关注置信目标。
Uncertainty Estimation:受贝叶斯网络中不确定性估计的启发,我们使用蒙特卡罗 Dropout 来估计不确定性
在随机 dropout 下对教师模型执行 T 次随机前向传递,并为每个输入量输入高斯噪声。
因此,对于输入中的每个体素,我们获得一组softmax概率向量:{pt}_t *T。我们选择 预测熵 作为近似不确定性的度量,因为它有一个固定的范围[8]。
采用预测熵,作为度量方式来近似获取到不确定性:UAMT 算法过滤掉分割预测中不确定值较高的像素,仅保留可信的像素作为学生模型学习的目标。
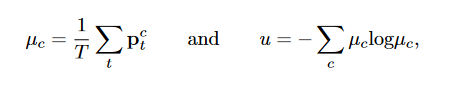
其中 ptc 是第 t 次预测中第 c 个类别的概率。请注意,不确定性是在体素水平上估计的,整个体积** U 的不确定性**是 {u} ∈ RH×W ×D。
Uncertainty-Aware Consistency Loss.:在估计不确定性 U 的指导下,我们过滤掉相对不可靠**(高不确定性)的预测,并仅选择某些预测作为学生模型学习的目标。特别是,对于我们的半监督分割任务,我们将不确定性感知一致性损失 Lc 设计为教师和学生模型的体素级均方误差(MSE)损失**,仅用于最确定的预测:
过滤掉高不确定性的,也就是熵大于某个值的。熵值越大,不确定性越高。
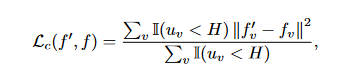
式中,I(·)为指示函数; f ′ v 和 fv 分别是教师模型和学生模型在第 v 个体素处的预测; uv 是第 v 个体素处的估计不确定性 U; H是选择最确定目标的阈值。
通过我们在训练过程中的不确定性感知一致性损失,学生和教师都可以学到更可靠的知识,从而减少模型的整体不确定性。