数理逻辑

定义

使用数学的方法研究逻辑推理的规律

命题

数理逻辑研究的中心问题是推理，而推理的前提和结论都是命题。因而命题是推理的基本单位。

定义

具有确切真值的陈述句称为命题(proposition)。该命题可以取一个“值”，称为真值。真值只有“真”和“假”两种，分别用“T”(或“1”)和“F”(或“0”)表示。

不是命题的例子

一切没有判断内容的句子都不是命题，比如命令句、疑问句、祈使句、二义性的陈述句。

• 命令句：比如，“把门关上。” 这是一个请求或指令，没有真假之分。

• 疑问句：例如，“你今天怎么样？” 这是一个问题，它没有表明任何可以验证的事实。

• 二义性的陈述句，比如：“这个命题是假的（指当前这个命题）”。

  • 如果这是一个真命题，那么这个命题确实是假的，那么这个命题到底是真还是假？
  • 如果这是一个假命题，那么这个命题不是假命题而是真命题，跟上面一样产生了矛盾。

原子命题和复合命题

定义

• 原子命题(简单命题)：不能再分解为更为简单命题的命题。
• 复合命题：可以分解为更为简单命题的命题。这些简单命题之间是通过如“或者”、“并且”、“不”、“如果…则……”、“当且仅当”等这样的逻辑连词和标点符号复合而成。

约定

通常用大写的带或不带下标的英文字母表示命题（包括原子命题和复合命题），例如：

$$A,B,C,\dots ,P,Q,R,\dots ,A_1,B_1,C_1,\dots ,P_1,Q_i,R_i,\dots$$

命题联结词

否定联结词

定义

设 P 是任意一个命题，复合命题“非 P”(或“P 的否定”)称为 P 的否定式 (negation)，记作 ¬P，其中 ¬ 为否定联结词。P 为真当且仅当 ¬P 为假。

例子

• P: 四川是一个国家。
• ¬P: 四川不是一个国家。

否定式是自然语言中的“非”、“不”、“没有”等的逻辑抽象。

真值表

P	¬P
真(T)	假(F)
假(F)	真(T)

这个真值表表示的是，如果原命题 P 的真值为真（T），那么它的否定 ¬P 的真值为假（F），反之亦然。

合取联结词

定义

设 P、Q 是任意两个命题，复合命题“P 并且 Q”(或“P 和 Q”)称为 P 与 Q 的合取式 (conjunction)，记作 P∧Q，其中 “∧” 为合取联结词。P∧Q 为真当且仅当 P，Q 同为真。

例子

• P: 3 是素数。
• Q: 3 是奇数。
• P∧Q: 3 既是素数又是奇数。

这展示了合取命题的性质：只有当所有单独的命题都为真时，合取命题才为真。

真值表

P	Q	P∧Q
真(T)	真(T)	真(T)
真(T)	假(F)	假(F)
假(F)	真(T)	假(F)
假(F)	假(F)	假(F)

这个真值表表示的是合取命题 P∧Q 只有在两个单个命题 P 和 Q 都为真的情况下才为真，如果其中任何一个为假，合取命题 P∧Q 就为假。

析取联结词

定义

设 P、Q 是任意两个命题，复合命题 “P 或 Q” 称为 P 与 Q 的析取式 (disjunction)，记作 P∨Q，其中 “∨” 是析取联结词。P∨Q 为真当且仅当 P、Q 至少有一个为真。

例子

• P: 张谦是大学生。
• Q: 张谦是运动员。
• P∨Q: 张谦是大学生或是运动员。

这个例子说明了析取命题 P∨Q 的性质：只要 P 和 Q 中至少有一个命题为真，P∨Q 就为真。

蕴含联结词

定义

设 P、Q 是任两个命题，复合命题 “如果 P，则 Q” 称为 P 与 Q 的蕴涵式 (implication)，记作 P → Q，其中 “→” 是蕴涵联结词。P → Q 为假当且仅当 P 为真且 Q 为假。一般把蕴涵式 P → Q 中的 P 称为该蕴涵式的前件，Q 称为蕴涵式的后件。

例子

• P: 周末天气晴朗。
• Q: 我们将到郊外旅游。
• P → Q: 如果周末天气晴朗，则我们将到郊外旅游。

这个例子阐明了蕴涵式 P → Q 的性质：只在 P 为真且 Q 为假的情况下，P → Q 才为假。

真值表

P	Q	P → Q
真(T)	真(T)	真(T)
真(T)	假(F)	假(F)
假(F)	真(T)	真(T)
假(F)	假(F)	真(T)

这个真值表表示的是蕴涵式 P → Q 的真值条件。只有当 P 为真而 Q 为假时，P → Q 才为假。在其他所有情况下，P → Q 都为真。

当前件P为假，无论后件Q真假如何， P → Q都为真，这被称为善意推定。打个比方，我们将“罪证为假”设定为P，“犯人无罪”设定为Q，那么，“如果罪证为假，则犯人无罪”设定为P → Q，显然，即使P这个命题是假的，也不影响P → Q为真。

等价联结词

定义

设 P、Q 是任两个命题，复合命题 “P 当且仅当 Q” 称为 P 与 Q 的等价式 (equivalence)，记作 P ↔ Q，其中 “↔” 是等价联结词（也称作双条件联结词）。P ↔ Q 为真当且仅当 P、Q 同为真或者同为假。

例子

• P: 两个三角形全等。
• Q: 三角形的三条边全部相等。
• P ↔ Q: 两个三角形全等当且仅当三角形的三条边全部相等。

这个例子表明了等价命题 P ↔ Q 的性质：它只在 P 和 Q 同时为真或同时为假的情况下为真。

真值表

P	Q	P ↔ Q
真(T)	真(T)	真(T)
真(T)	假(F)	假(F)
假(F)	真(T)	假(F)
假(F)	假(F)	真(T)

此真值表描述了等价联结词 P ↔ Q 的逻辑行为：当 P 和 Q 都为真或都为假时，P ↔ Q 是真；当 P 和 Q 之一为真而另一为假时，P ↔ Q 是假。

命题符号化及其应用

速查表格

联结词	记号	复合命题	读法	记法	真值结果
否定	$\neg$	$\neg P$	非 P	P 的否定	-P 的真值为“真”当且仅当 P的真值为“假”
合取	$\wedge$	$P\wedge Q$	P 并且 Q	P 合取 Q	$P\wedge Q$ 的真值为“真"当且仅当 P、Q 的真值同为“真”
析取	$\vee$	$P\vee Q$	P 或者 Q	P 析取 Q	$P\vee Q$ 的真值为“真”当且仅当 P、Q 的真值至少一个为“真”
蕴涵	$\to$	$P\to Q$	若 P，则 Q	P 蕴涵 Q	$P\to Q$ 的真值为“假”当且仅当 P的真值为“真”、Q 的真值为“假”
等价	$\leftrightarrow$	$P\leftrightarrow Q$	当且仅当 Q	P 等价于 Q	$P\leftrightarrow Q$ 的真值为“真”当且仅当 P、Q 的真值同为“真”或同为“假”

注意：

• $\wedge$与$\vee$还有$\leftrightarrow$是有对称性的，而$\neg$和$\to$没有。

• 联结词是两个命题真值之间的联结，而不是命题内容之间的连接，因此复合命题的真值只取决于构成他们的各简单命题的真值，而与它们的内容无关，与二者之间是否有关系无关。

优先级

所有五个联接词的优先顺序（数字越小越优先）为

1. 否定
2. 合取
3. 析取
4. 蕴涵
5. 等价

• 同级的联结词，按其出现的先后次序(从左到右)；

• 若运算要求与优先次序不一致时，可使用括号；

• 同级符号相邻时，也可使用括号。括号中的运算为最高优先级。

在大多数编程语言中，否定（表现为!或者not）、合取（&&或者and）、析取（||或者or），这一顺序同样适用。

复合命题符号化

假设有命题：

• P: 你陪伴我
• Q: 你代我叫车子
• R: 我将出去

下面是这些语句的符号化表示：

1. 如果你陪伴我并且代我叫辆车子，则我将出去。

   • 符号化为: $(P\wedge Q)\to R$

2. 如果你不陪伴我或不代我叫辆车子，我将不出去。

   • 符号化为: $(\neg P\vee \neg Q)\to \neg R$

3. 除非你陪伴我或代我叫车子，否则我将不出去。

   • 符号化为: $(\neg P\wedge \neg Q)\to \neg R$ 或者可以表示为 $\neg (P\vee Q)\to \neg R$，依据德摩根定律。如果不使用否定符号，还可以写$R\to (P\vee Q)$，也就是反过来。

布尔检索演示

1. 同时包含“量子物理”和“弦理论”

   • Google搜索框输入: 量子物理 AND 弦理论
   • 数学符号表达式: $量子物理\wedge 弦理论$

2. 包含“量子物理”但不包含“弦理论”

   • Google搜索框输入: 量子物理 -弦理论
   • 数学符号表达式: $量子物理\wedge \neg 弦理论$

3. 包含“量子物理”或“相对论”

   • Google搜索框输入: 量子物理 OR 相对论
   • 数学符号表达式: $量子物理\vee 相对论$

命题变元

一个特定的命题是一个常值命题，不是真就是假。

一个任意的没有赋予具体内容的原子命题是一个变量命题，常称为命题变量（命题变元），无具体真值。

当原子命题是命题变元，包含此原子命题的复合命题也即命题变元的函数，该函数称为真值函数或者命题公式。

如下是一个命题函数：
$$G=P\wedge Q\to \neg R$$

命题公式

命题演算的合式公式（well formed formula, wff），又称为命题公式，简称公式。

有三条规则生成合式公式：

1. 命题变元本身是一个公式。
2. G是公式，则$(\neg G)$也是公式
3. 如G、H是公式，$(G\wedge H)$是公式，诸如此类都是公式

由有限步使用上述三个规则后得到的符号串才是命题公式。

• 原子命题变元是最简单的合式公式，称为原子合式公式，简称原子公式。
• 命题公式没有真值，只有对命题变元进行真值指派后才可确定真值。
• 整个公式最外层括号可以省略，不影响运算次序的括号也可省略。
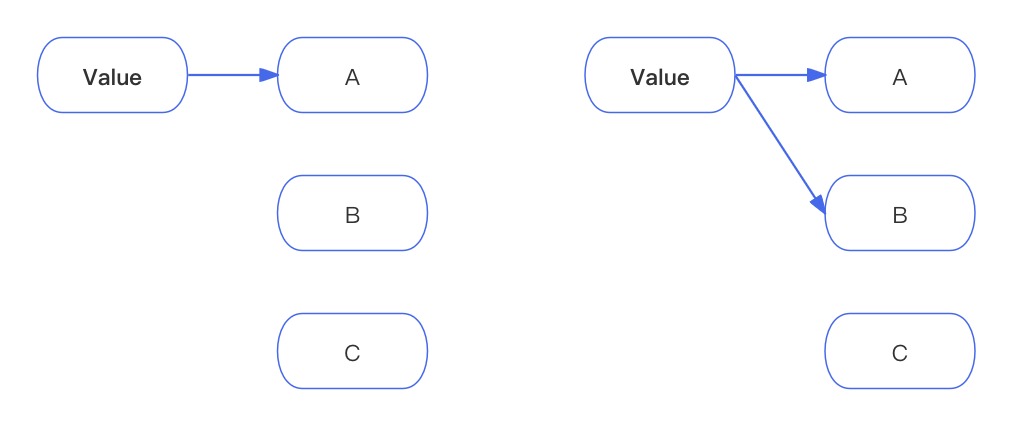
• 可以使用二元树的方式表达，如下图。

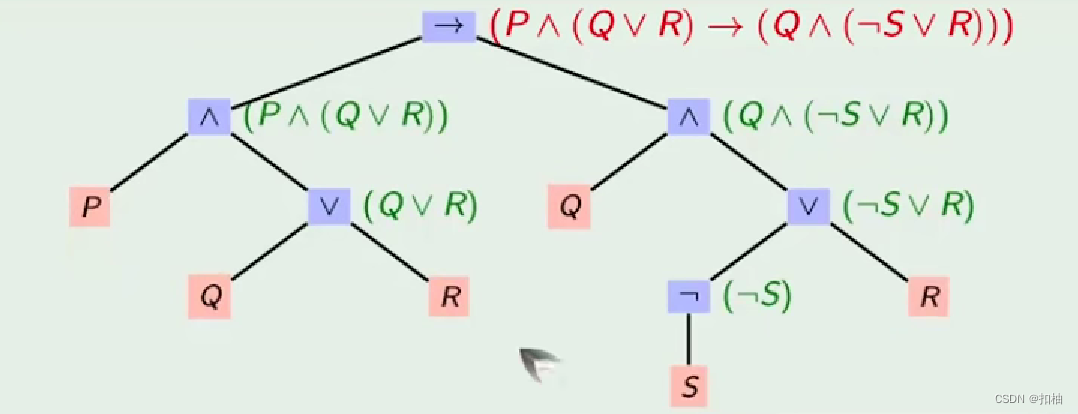
公式的解释

设$P_1,P_2,P_3...,P_n$是出现在公式$G$中的所有命题变元，指定$P_1,P_2,P_3...,P_n$的一组真值，这组真值称为$G$的一个解释，常记为$I$。

如果公式在解释$I$下为真，称$I$为$G$的成真赋值，为假则称为成假赋值。

真值表

一般来说，如果有$n$个命题变元，则有$2^n$个不同解释。

由公式$G$在其所有可能解释下所取真值构成的表，称为$G$的真值表。

真值表画法：

示例真值表：

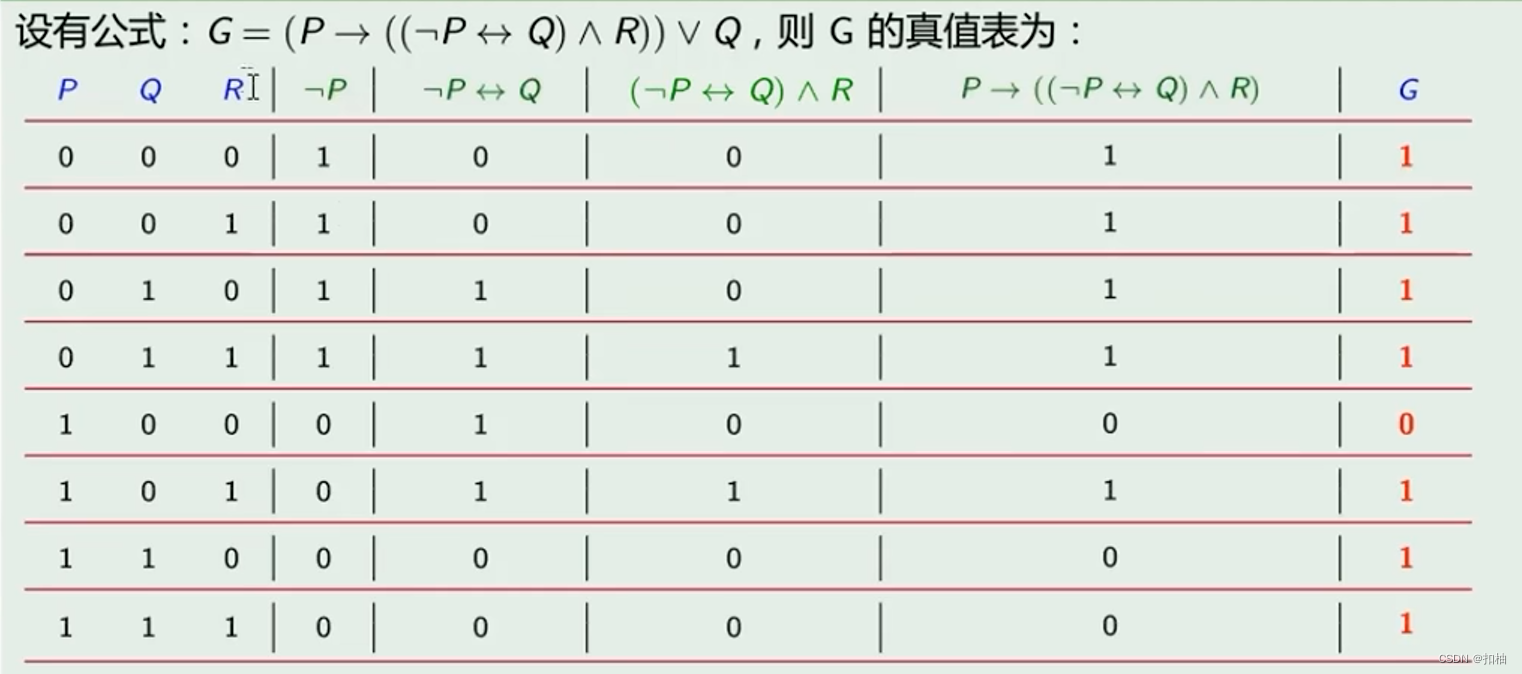
命题公式的分类

1. 永真公式（重言式, tautology）：公式的所有解释下真值都为真。
2. 永假公式（矛盾式, contradiction）：公式的所有解释下真值都为假。
3. 可满足公式（satisfiable），在此公式不是永假公式的情况下，永真公式一定是可满足公式。

公式的逻辑等价

定义

对于两个命题公式$G,H$，如果它们的命题变元是$P_1,P_2,P_3...P_n$，那么对应的有$2^n$个解释，如果这些解释中，G和H的真值结果全都相同，则称G和H为等价的，记作$G=H$（或者$G\iff H$）。

定理

$G=H$的充分必要条件为：$G\leftrightarrow H$是永真公式。

可判定性：可完成对任意公式的判定类问题，命题公式是可判定的。（类型或等价判定）

命题公式的逻辑律、基本等价关系

有了这些逻辑律和等价关系，我们就可以进行巧妙地证明、化简、求解了。

可用于化简门电路、化简判断逻辑来进行优化性能。

幂等律 (Idempotent Laws)

• 逻辑与的幂等律：$G\wedge G\equiv G$
• 逻辑或的幂等律：$G\vee G\equiv G$

交换律 (Commutative Laws)

• 逻辑与的交换律：$G\wedge H\equiv H\wedge G$
• 逻辑或的交换律：$G\vee H\equiv H\vee G$

结合律 (Associative Laws)

• 逻辑与的结合律：$(G\wedge H)\wedge I\equiv G\wedge (H\wedge I)$
• 逻辑或的结合律：$(G\vee H)\vee I\equiv G\vee (H\vee I)$

同一律 (Identity Laws)

• 逻辑与的同一律：$G\wedge \text{True}\equiv G$
• 逻辑或的同一律：$G\vee \text{False}\equiv G$

零律 (Domination Laws)

• 逻辑与的零律：$G\wedge \text{False}\equiv \text{False}$
• 逻辑或的零律：$G\vee \text{True}\equiv \text{True}$

分配律 (Distributive Laws)

• 逻辑与对逻辑或的分配律：$G\wedge (H\vee I)\equiv (G\wedge H)\vee (G\wedge I)$
• 逻辑或对逻辑与的分配律：$G\vee (H\wedge I)\equiv (G\vee H)\wedge (G\vee I)$

吸收率 (Absorption Laws)

• 逻辑与的吸收率：$G\wedge (G\vee H)\equiv G$
• 逻辑或的吸收率：$G\vee (G\wedge H)\equiv G$

矛盾律 (Contradiction Law)

• $G\wedge \neg G\equiv \text{False}$

排中律 (Law of Excluded Middle)

• $G\vee \neg G\equiv \text{True}$

双重否定律 (Double Negation Law)

• $\neg (\neg G)\equiv G$

德摩根律 (De Morgan’s Laws)

• $\neg (G\wedge H)\equiv \neg G\vee \neg H$
• $\neg (G\vee H)\equiv \neg G\wedge \neg H$

蕴含式 (Implication)

• $G\to H\equiv \neg G\vee H$

假言易位 (Contrapositive)

• $(G\to H)\equiv (\neg H\to \neg G)$

等价式 (Equivalence)

• $(G\leftrightarrow H)\equiv (G\to H)\wedge (H\to G)$

等价否定式 (Negation of Equivalence)

• $(G\leftrightarrow H)\equiv \neg G\leftrightarrow \neg H$

归谬论 (Reductio ad absurdum)

• $(\neg G\to \text{False})\to G$

范式 (Normal Form)

• 有限个简单合取式（短语）的析取称为析取范式（disjunctive normal form）。
• 有限个简单析取式（子句）的合取成为合取范式（conjunctive normal form）。

文字 (Literal)

命题变元和命题变元的否定都是文字。

例如，在表达式 $(p\vee \neg q)$ 中，$p$ 和 $\neg q$ 都是文字。

子句 (Clause)

有限个文字的析取成为简单析取式（或子句）。

短语 (Phrase)

有限个文字的合取成为简单合取式（或短语）。