二叉树和堆

- 一、树的概念和结构
- 二、二叉树的概念
- 三、堆
- 四、堆的创建
- - one、堆的插入(需要与向上或者向下调整算法配合(取决于你建大堆还是小堆)
  - two、剔除堆中的根节点
- 五、堆的简单排序

一、树的概念和结构

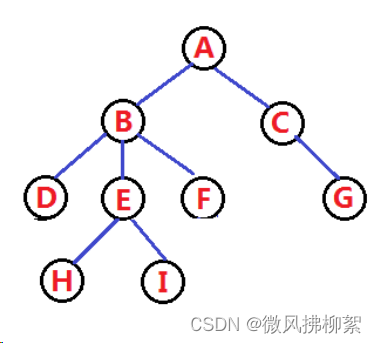
树是一种非线性的的数据结构，逻辑结构就是一颗倒挂的树，物理结构是一个数组

这里的A为父亲，B和C为孩子，以此类推D,E,F是B的孩子

二、二叉树的概念

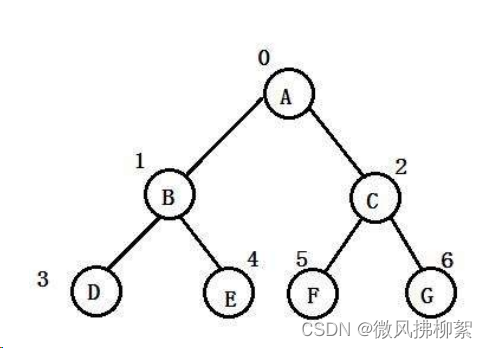
1.二叉树是有限个节点的集合，根节点就是数组的第一个元素array[0]，根节点下面分为左子树和右子树

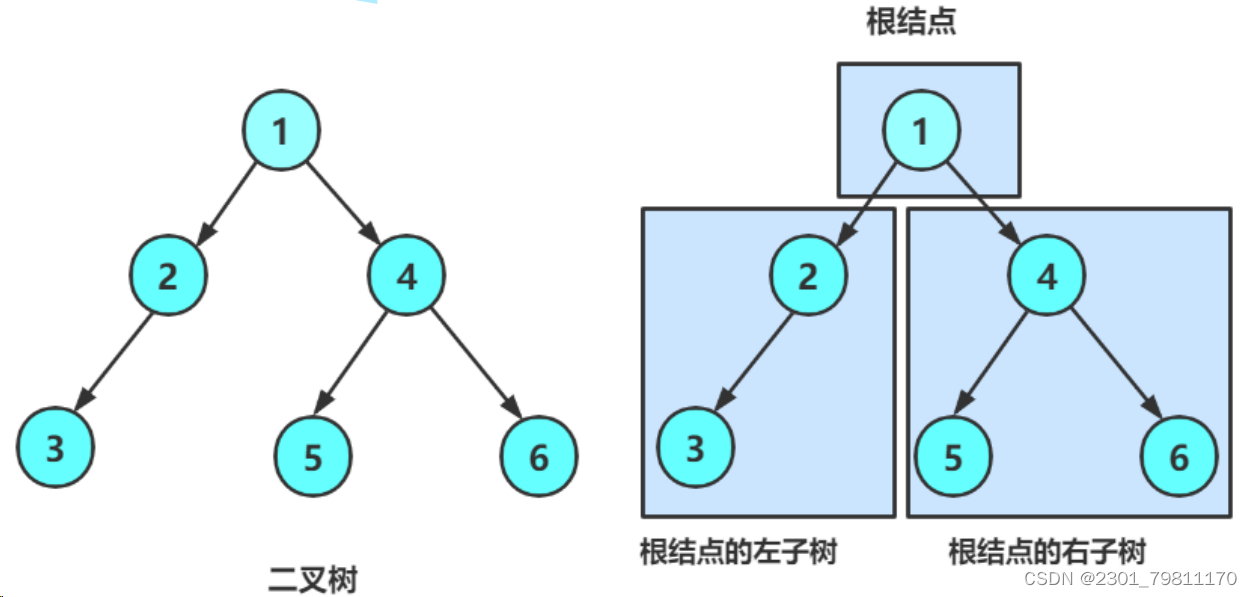
2.特殊的二叉树：

满二叉树
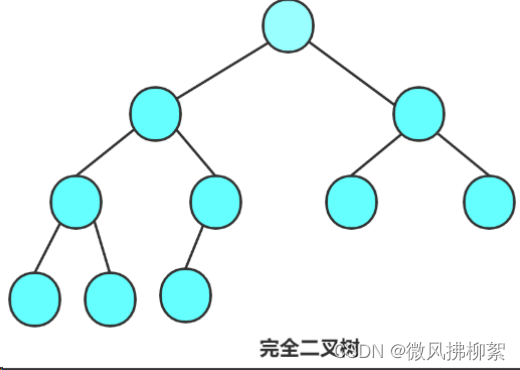
完全二叉树

三、堆

堆分为小堆和大堆

小堆的父亲小于或等于孩子
大堆的父亲大于或等于孩子

堆总是一颗完全二叉树

四、堆的创建

这里有些部分与顺序表非常相似
比如

堆的初始化
堆的销毁
判断堆是否为空
找出堆中的首元素

one、堆的插入(需要与向上或者向下调整算法配合(取决于你建大堆还是小堆)

我这里是建小堆
用的向上调整算法

void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){HPDataType tmp = a[parent];a[parent] = a[child];a[child] = tmp;child = parent;parent = (child - 1) / 2;}else{break;}}}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = (php->capacity == 0 ? 4 : php->capacity * 2);HPDataType* tmp = (HPDataType*)realloc(php->a,newcapacity*sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a,php->size-1);
}

下面是向下调整算法：用于建大堆

void AdjustDown(HPDataType* a, int size)
{int parent = 0;int child = parent * 2 + 1;while (child < size){ if (child+1<size && a[child] > a[child + 1]){child++;}if (a[parent] > a[child]){HPDataType tmp = a[parent];a[parent] = a[child];a[child] = tmp;parent = child;child = parent * 2 + 1;}else{break;}}}

two、剔除堆中的根节点

这里需要讲根节点和堆中最后一个元素交换位置

然后再将交换之后的堆的尾元素剔除，然后重新调整堆，需要用到向下调整算法

void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));//判断size不为0if (php->size > 0){HPDataType tmp = php->a[0];php->a[0] = php->a[php->size - 1];php->a[php->size - 1] = tmp;php->size--;AdjustDown(php->a,php->size);}else{perror("HeapPop fail");return;}
}

五、堆的简单排序

void HeapSort(HPDataType* a, int n)
{//升序 -- 建大堆//降序 -- 建小堆//建堆 向上调整建堆for (int i = 1; i < n; i++){AdjustUp(a,i);}int end = n - 1;while (end > 0){HPDataType tmp = a[0];a[0] = a[end];a[end] = tmp;end--;}
}