目录

Softmax回归

损失函数

图片分类数据集

Softmax回归从零开始实现

Softmax回归简洁实现

---

Softmax回归

回归和分类的区别

回归问题举例上节课的预测房价问题，分类问题就是对样本进行分类

回归和分类的具体区别

假设真实的类别为第i个类别（值为1），其他类别都是假的（值为0），选择i最大化置信度

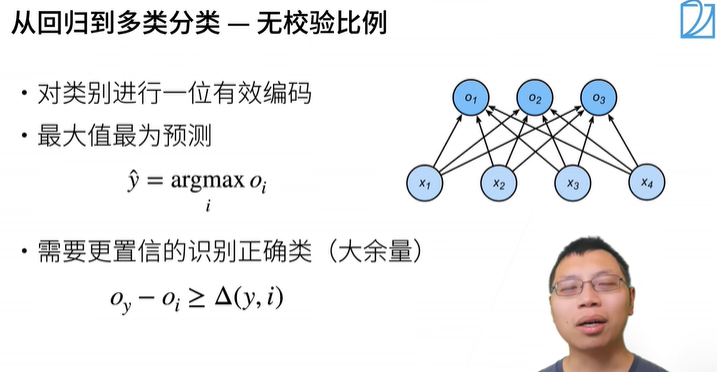
置信度的规则

选择i使得置信度远大于其他的类别的置信度

置信度相当于概率

y hat是一个长为n的向量 下面那个公式的操作是使得和为1，也就是说yi hat可以作为概率，两个Y的区别就可以作为损失

softmax的损失函数

softmax回归总结

损失函数

均方损失

蓝色：Y=0时，变化预测值Y’的函数（二次函数）

绿色：似然函数（高斯分布）

橙色：损失函数的梯度（穿过原点的一次函数），决定了如何更新参数

梯度和预测值的相对关系决定了参数更新的变化程度

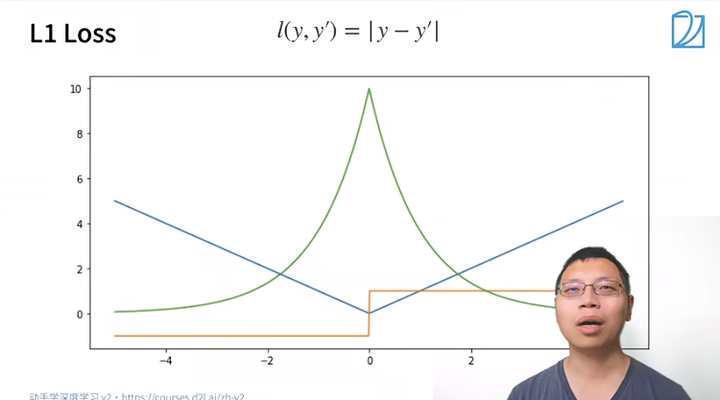
L1损失函数

蓝色：预测值、绿色：似然函数、橙色：导数

好处：稳定

不好：零点处不可导

综合以上两种损失函数，自己造的完美损失函数

梯度和实际值的相对关系

---

图片分类数据集

Fashion-MNIST数据集

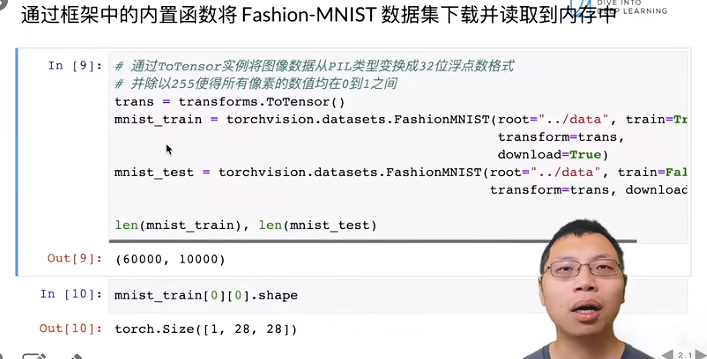
下载数据集到内存

transforms.totensor() 将图像数据转化为浮点数格式

train=true 下载训练数据集 download=true默认在网上下载

第一张图片的形状 1表示Channel 28x28

打标签、输出图像函数

输出

画两行，每行有九张图片

读取数据

shuffle 决定是否要打乱数据集的顺序

timer用来测试速度（读取数据的速度通常要比模型速度快很多）

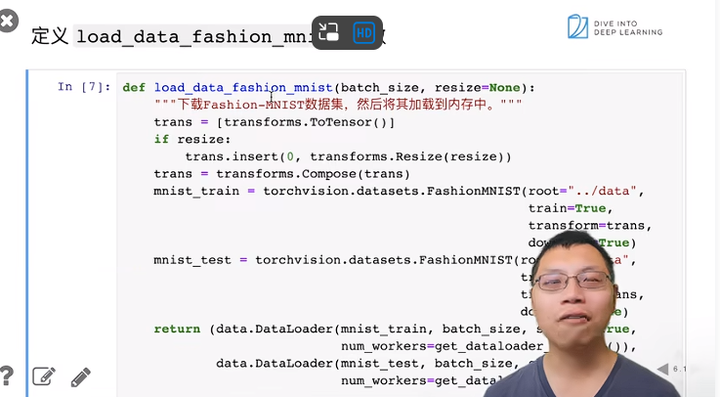
下载数据集

resize可以选择把图片变得更大

---

Softmax回归从零开始实现

softmax是所有深度学习的基础

iter 训练集和测试集的迭代器

拉成向量（会损失信息，可以用卷积神经网络恢复）

矩阵求和

keepdim=true 表示还是二维矩阵 X是一个矩阵

实现softmax

一个实例

实现softmax回归模型

-1表示自动计算（实际表示批量大小）

举个例子

y_hat是预测值

y_hat [ [0,1], y] 拿出对真实标号那个类的预测值

实现交叉熵损失函数

预测类别与真实元素进行比较

评估任意模型的准确率

Accumulator

softmax回归训练

可视化

训练函数

优化损失函数

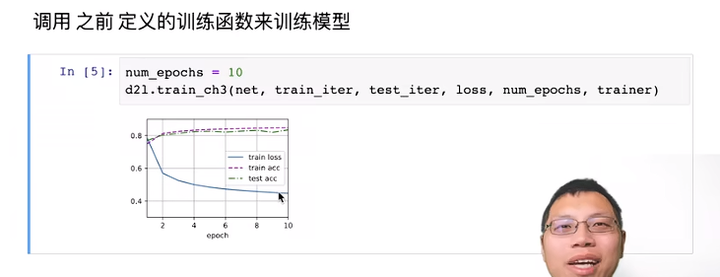
训练模型

对图片进行分类预测

Softmax回归简洁实现