堆排序的时间复杂度是O（N*logN），优于选择排序O（N^2）

一、堆

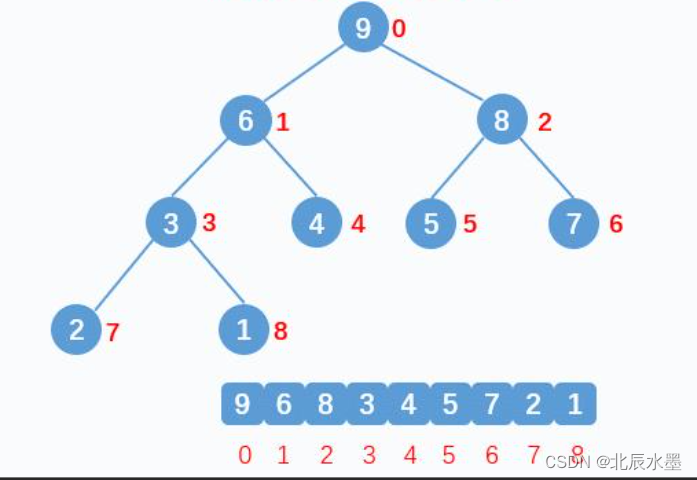
1.堆的概念：堆一般指的是二叉堆，顾名思义，二叉堆是完全二叉树或者近似完全二

2.堆的性质：①完全二叉树

                     ②每个节点的值都大于或等于其子节点的值，为最大堆；反之为最小堆。

3.堆的存储结构是数组，逻辑结构是二叉树

二、 堆排序（包括建堆和排序）：

1.建堆的实现原理：

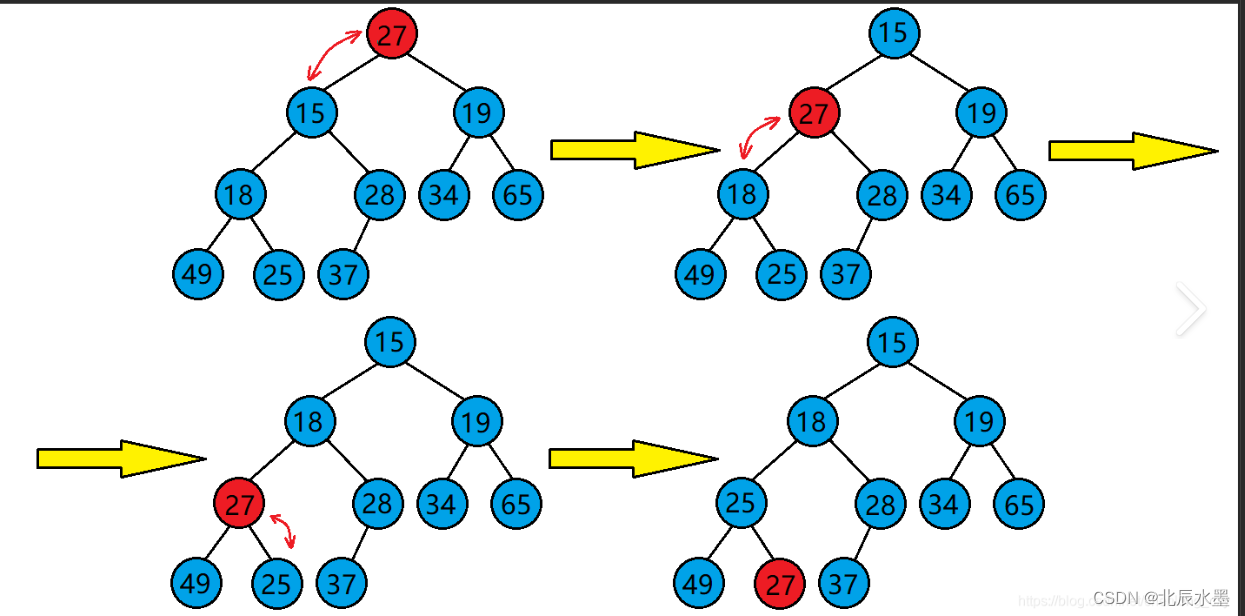
用到向下调整算法，比较两个孩子的大小，选出大的孩子，与父亲比较，如果孩子大于父亲，交换。然后把parent=child，child=parent*2+1；向下调整算法一共会调整h-1次，因此时间复杂度是O（logN）

从最后一个非叶子的节点开始用向下调整算法，实现建大堆。（建小堆就是> < 符号的改变）

2.向下调整算法的过程：

void swap(int* a, int* b)//实现交换的函数
{int tmp = *a;*a = *b;*b = tmp;
}
//前提下面都是大堆
void AdjustDown(int* a, int n,int root)//向下调整算法
{int parent = root;int child = parent * 2 + 1;//默认是左孩子，逻辑结构中二叉树的一个规律，左孩子=父亲*2+1while (child < n){if (child+1<n && a[child] < a[child+1])//排大堆，如果右孩子更大，就让child是右孩子{child += 1;}if (a[child] > a[parent])//排大堆，如果孩子大于父亲，交换，并且依次向下调整{swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else//已经是大堆了，退出while循环{break;}} 

 3.建堆：

//建堆：从最后一个非叶子节点开始调整，就可以达到下面都是大堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)//n-1是最后一个数组下标，求父亲(下标-1)/2
{AdjustDown(arr, n, i);
}

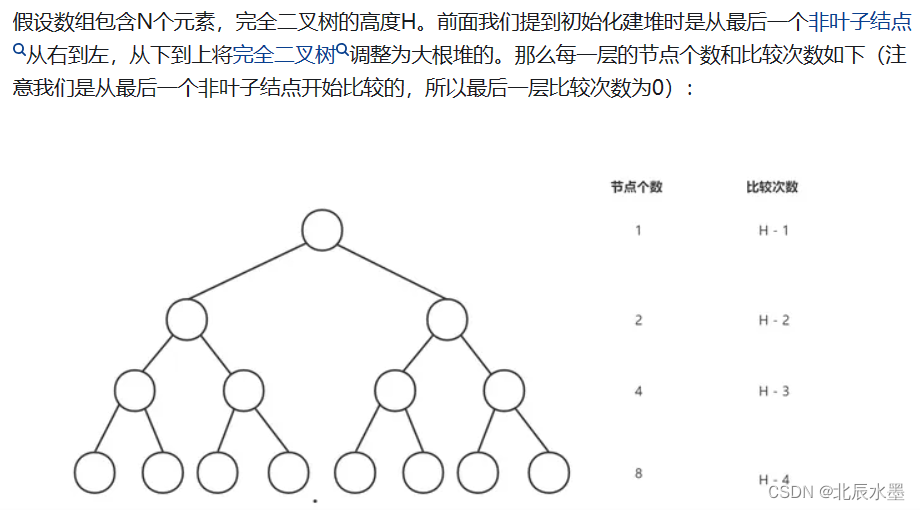
4.建堆的时间复杂度是O（N）-->（粗略的了解原理，记住结论就行）

 5.排序：（用大堆）

用小堆的坏处：交换之后踢出第一个数，会导致堆的错位，要重新建堆，时间复杂度O（N^2）

排序的原理：

把第一个最大的数与最后一个数交换，然后把最后一个数踢出堆，继续向下调整算法，再交换次大的数。

int end = n - 1;
while (end > 0)
{swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);//把交换之后的根，向下调整，调整h-1次，又变成大堆，再交换，可以得到次小的数end--;
}

堆排序的所有代码：

#include<stdio.h>
void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
//前提下面都是大（小）堆
void AdjustDown(int* a, int n,int root)
{int parent = root;int child = parent * 2 + 1;//默认是左孩子while (child < n){if (child+1<n && a[child] < a[child+1])//排大堆{child += 1;}if (a[child] > a[parent])//排大堆{swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}} 
}
void HeapSort(int* arr, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--)//n-1是最后一个数组下标，求父亲(下标-1)/2{AdjustDown(arr, n, i);}int end = n - 1;while (end > 0){swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);//把交换之后的根，向下调整，调整h-1次，又变成大堆，再交换，可以得到次小的数end--;}
}
int main()
{int arr[] = { 10,1,5,3,6,8,7,4,9};int n = sizeof(arr) / sizeof(arr[0]);HeapSort(arr, n);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}return 0;
}