轮廓系数(Silhouette Coefficient)是评估聚类算法效果的常用指标之一。它结合了聚类的凝聚度(Cohesion)和分离度(Separation),能够量化聚类结果的紧密度和分离度。
背景
1.聚类分析的背景
在数据挖掘和机器学习领域,聚类分析是一种常用的无监督学习方法,用于将数据集中的对象划分为具有相似特征的簇。聚类分析的目标是发现数据中的内在结构,将相似的数据点归为一类,并使不同类别之间的差异最大化。通过聚类,我们可以识别出数据中的模式、群集和关联,从而进行进一步的分析和决策制定。
2.评估聚类效果的需求
在进行聚类分析时,评估聚类效果是至关重要的。一个好的聚类结果应该具有以下特征:
簇内的样本应该尽可能相似。
不同簇之间应该尽可能不相似。
因此,我们需要一种评估指标来衡量聚类的紧密度和分离度,以便对不同的聚类结果进行比较,并选择最佳的聚类数目和算法。
3.轮廓系数的产生
轮廓系数是由Peter J. Rousseeuw 在1987年提出的。它的提出是为了克服传统的聚类评估方法的局限性,如仅仅依赖于簇内的均方差来评估聚类效果。轮廓系数的目的是同时考虑簇内和簇间的距离,从而提供更全面的聚类质量评估。轮廓系数是一种相对直观且易于理解的指标,它将聚类的紧密度和分离度结合在一起,提供了对聚类质量的综合评价。它的取值范围在-1到1之间,值越接近1表示聚类效果越好,值越接近-1表示聚类效果越差。
定义
轮廓系数通过计算每个数据点的轮廓系数来评估聚类的质量。轮廓系数的计算基于以下两个因素:
-
簇内相似度(凝聚度)(a):数据点与同一簇内其他点的平均距离。它衡量了数据点与其所属簇的紧密程度。
-
簇间不相似度(分离度)(b):数据点与其最近的不同簇的所有点的平均距离。它衡量了数据点与其他簇的分离程度。
计算过程
对于每个数据点i,其轮廓系数 s i s_i si可以通过以下公式计算:
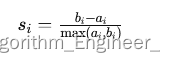
其中,
a i a_i ai 是数据点i与其所属簇内其他点的平均距离。
b i b_i bi 是数据点i与最近的不同簇中所有点的平均距离。
对于整个数据集,轮廓系数SS是所有数据点的轮廓系数的平均值。
解释
轮廓系数的取值范围在-1到1之间。
当轮廓系数接近1时,表示簇内相似度高,簇间不相似度低,聚类效果好。
当轮廓系数接近0时,表示簇内相似度和簇间不相似度相当,聚类效果一般。
当轮廓系数接近-1时,表示簇内相似度低,簇间不相似度高,聚类效果差。
优缺点
优点:能够同时考虑簇内和簇间的距离,提供了对聚类质量的全面评估。易于理解和计算,适用于各种类型的聚类算法。缺点:对聚类形状和密度不敏感,可能无法有效地处理非凸形状的簇或密度不均匀的簇。受到数据集不均衡的影响,可能导致评估结果不准确。
应用
轮廓系数广泛应用于各种聚类算法的性能评估和比较,如K均值聚类、层次聚类、DBSCAN等。它也被用于确定最佳的聚类数目和帮助解释聚类结果。