【查找算法】二分查找

一：二分查找

1.1 基本概念

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

1.2 原理

查找的目标数据元素必须是有序的。没有顺序的数据，二分法就失去意义。
数据元素通常是数值型，可以比较大小。
将目标元素和查找范围的中间值做比较（如果目标元素=中间值，查找结束），将目标元素分到较大/或者较小的一组。
通过分组，可以将查找范围缩小一半。
重复第三步，直到目标元素=新的范围的中间值，查找结束。

1.3 基本思想

首先用要查找的关键字key与中间位置的结点的关键字相比较，这个中间结点把线性表分成了两个子表，若比较结果相等则查找完成；若不相等，再根据k与该中间节点关键字的的比较大小来去确定下一步查找哪个子表（如果我们把一个线性表想成是水平的，如果key值大于中间节点，则在右边的子表继续查找；如果key值小于中间值，则在左边的子表继续查找），这样递归下去，直到找到满足条件的节点或者该线性表中没有这样的节点。

1.4 图解

第一步：
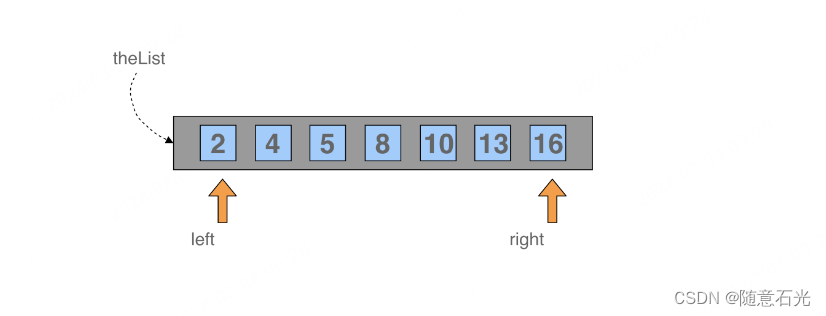
在这里插入图片描述
第二步：

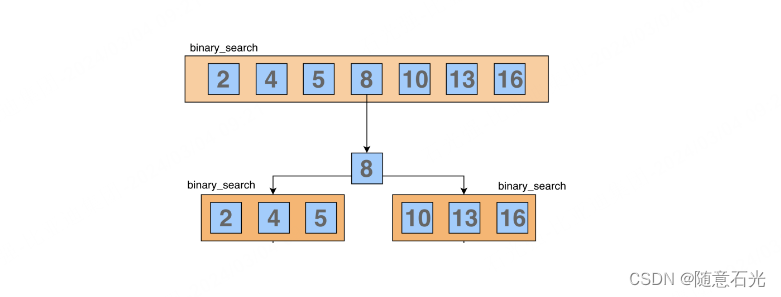
第三步：

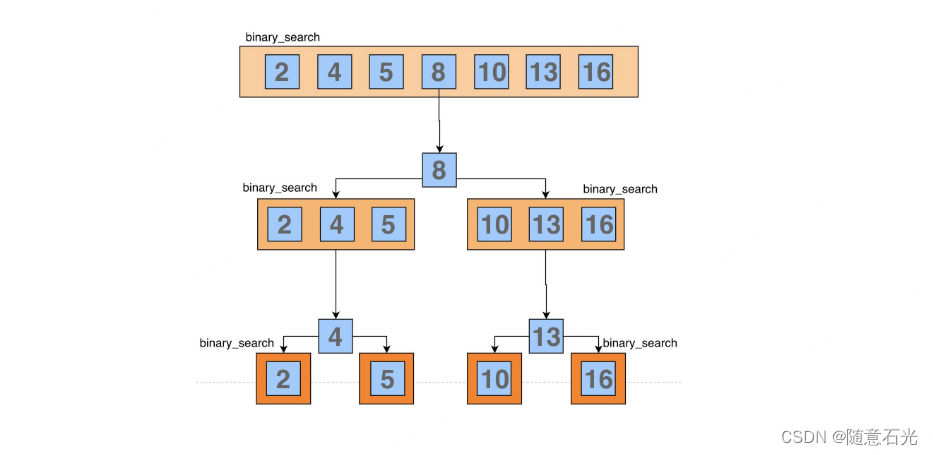
1.5 优缺点

优点：

比较次数少，查找速度快，平均性能好。

缺点：

必须要求待查表为有序表（若为无序数组，分成两份查找没有意义，排序本身也要耗费时间）；
插入删除困难（曾删操作需要移动大量的节点）

二：时间以及空间复杂度

2.1 时间复杂度分析

最坏的情况下：两种方式时间复杂度一样：O(log2 N)
最好情况下： O（1）

2.2 空间复杂度分析

算法的空间复杂度并不是计算实际占用的空间，而是计算整个算法的辅助空间单元的个数

2.2.1 循环方式

由于辅助空间是常数级别的所以：空间复杂度是O(1);

2.2.2 递归方式

递归的次数和深度都是log2 N,每次所需要的辅助空间都是常数级别的：空间复杂度：O(log2N )

三：代码实现

3.1 基本写法

/*** 二分查找* 注意：使用二分查找必须保证该数组是有序的*/
public class BinarySearch {public static void main(String[] args) {int[] array = {1, 8, 10, 89, 1000, 1234};int index = binarySearch(array, 0, array.length - 1, 1);System.out.println(index);}/*** 二分查找算法** @param array     原始数组* @param right     右节点* @param left      左节点* @param findValue 需要查找的值* @return 需要查找值的下标，如果没找到就返回-1*/public static int binarySearch(int[] array, int right, int left, int findValue) {//获取中间值的下标int middle = (right + left) / 2;//获取中间值int middleValue = array[middle];//当findValue小于最小值或者大于最大值的时候，表示没有找到当前数，返回-1表示未找到if (findValue < array[0] || findValue > array[array.length - 1] || left > right) {return -1;}if (findValue > middleValue) {//如果需要查找的值大于中间值，则向右递归return binarySearch(array, middle + 1, left, findValue);} else if (findValue < middleValue) {//如果需要查找的值小于中间值，则向左递归return binarySearch(array, right, middle - 1, findValue);} else {return middle;}}}

3.2 代码升级

问题：当一个有序数组中，有多个相同的数值时，如：{1,8, 10, 89, 1000, 1000，1234} 。如何将所有的数值都查找到，比如这里的 1000

package com.sysg.dataStructuresAndAlgorithms.find;import java.util.ArrayList;
import java.util.List;/*** 二分查找* 注意：使用二分查找必须保证该数组是有序的*/
public class BinarySearch {public static void main(String[] args) {int[] array = {1, 8, 10, 89, 1000, 1000, 1000, 1000, 1234};int index = binarySearch(array, 0, array.length - 1, 1000);System.out.println(index);List<Integer> indexPlus = binarySearchPlus(array, 0, array.length - 1, 1000);System.out.println(indexPlus);}/*** 二分查找算法（基础版本）** @param array     原始数组* @param right     右节点* @param left      左节点* @param findValue 需要查找的值* @return 需要查找值的下标，如果没找到就返回-1*/public static int binarySearch(int[] array, int left, int right, int findValue) {//获取中间值的下标int middle = (right + left) / 2;//获取中间值int middleValue = array[middle];//当findValue小于最小值或者大于最大值的时候，表示没有找到当前数，返回-1表示未找到if (findValue < array[0] || findValue > array[array.length - 1] || left > right) {return -1;}if (findValue > middleValue) {//如果需要查找的值大于中间值，则向右递归return binarySearch(array, middle + 1, right, findValue);} else if (findValue < middleValue) {//如果需要查找的值小于中间值，则向左递归return binarySearch(array, left, middle - 1, findValue);} else {return middle;}}/*** 二分查找算法（升级版本）* 问题：当一个有序数组中，有多个相同的数值时，如：{1,8, 10, 89, 1000, 1000，1234} 。如何将所有的数值都查找到，比如这里的 1000* 思路分析：* 1.再找到middle的索引值后不要马上就返回* 2.向索引值的左边进行扫描，将所有符合条件的索引下标放入到arrayList当中* 3.向索引值的右边进行扫描，将所有符合条件的索引下标放入到arrayList当中* 4.最后返会arrayList** @param array     原始数组* @param right     右节点* @param left      左节点* @param findValue 需要查找的值* @return 需要查找值的下标，如果没找到就返回-1*/public static List<Integer> binarySearchPlus(int[] array, int left, int right, int findValue) {//获取中间值的下标int middle = (right + left) / 2;//获取中间值int middleValue = array[middle];//当findValue小于最小值或者大于最大值的时候，表示没有找到当前数，返回-1表示未找到if (findValue < array[0] || findValue > array[array.length - 1] || left > right) {return new ArrayList<>();}if (findValue > middleValue) {//如果需要查找的值大于中间值，则向右递归return binarySearchPlus(array, middle + 1, right, findValue);} else if (findValue < middleValue) {//如果需要查找的值小于中间值，则向左递归return binarySearchPlus(array, left, middle - 1, findValue);} else {List<Integer> resultIndexList = new ArrayList<>();//向左边扫描//定义一个临时的值来记录middle左边的值int temp = middle - 1;//退出while (temp >= 0 && array[temp] == findValue) {//否则就将temp放入到arrayList当中resultIndexList.add(temp);//将temp左移继续判断temp -= 1;}resultIndexList.add(middle);//向右边扫描temp = middle + 1;//退出while (temp <= array.length - 1 && array[temp] == findValue) {//否则就将temp放入到arrayList当中resultIndexList.add(temp);//将temp左移继续判断temp++;}return resultIndexList;}}}