一、定义：

        为了避免搜索二叉树的高度增长过快，降低二叉树的性能，规定在插入和删除二叉树的结点的时候，任何结点左右子树的高度差绝对值不超过1，这样的二叉树被称为平衡二叉树（balanced Binary Tree），简称平衡树。在搜索二叉树BST的基础上增加以上性质，就称为AVL树。

二、AVL树的构造

      1. AVL树的结点是一个三叉链结构：相比BST多了一个指向parent的结点。

template<class K,class V>
struct AVLTreeNode {pair<K,V> _kv;//结点值AVLTreeNode* _parent;//指针，三叉链AVLTreeNode* _left;AVLTreeNode* _right;int _bf;//平衡因子AVLTreeNode(const pair<K,V> kv):_kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr), _bf(0){}
};

  2.AVL树的插入：

1. 首先，从根结点开始，与待插入结点比较大小，直到直到插入位置——叶子结点的空孩子指针，然后建立新结点，并与父节点链接。
2. 然后修改插入结点的父节点的平衡因子，左节点插入，平衡因子-1，反之，加1。
3. 父节点平衡因子修改后，分三种情况处理：

①父节点平衡因子为0，不用处理return。

②父节点平衡因子为±1，向上传递，回到第二步，此时cur=parent，parent=grantparent，根据cur和parent的位置关系，修改平衡因子。

③父节点平衡因子为±2，根据插入结点cur、parent以及grandparent的位置，分4种情况，进行4种旋转结束。

 3.AVL树的四种旋转

右单旋：条件为

条件为：if (parent->_bf == 2 && cur->_bf == 1)

 所有情况下的结构图如下：h>=0

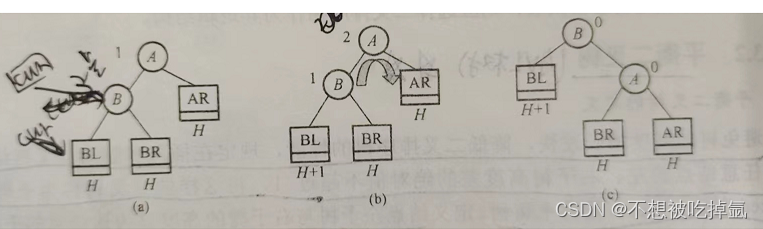
	void rotateR(Node* parent){Node* cur = parent->_left;Node* cur_right = cur->_right;parent->_left = cur_right;		//旋转第一步parent和cur_right的链接;if (cur->_right != nullptr)//Xcur_right->_parent = parent;cur->_right = parent;		//再处理cur和parent的链接Node* parent_parent = parent->_parent;//保存结点，用于处理，cur->parent;parent->_parent = cur;if (parent == _root)		//处理cur和parent_parent的链接{_root = cur;cur->_parent = nullptr;//X}else {cur->_parent = parent_parent;if (parent_parent->_left == parent){parent_parent->_left = cur;}else {parent_parent->_right = cur;}}parent->_bf = 0;//旋转后平衡因子为0cur->_bf = 0;}

左单旋：

条件为：if(parent->_bf==2&&cur->_bf==1)

  所有情况下的结构图如下：h>=0

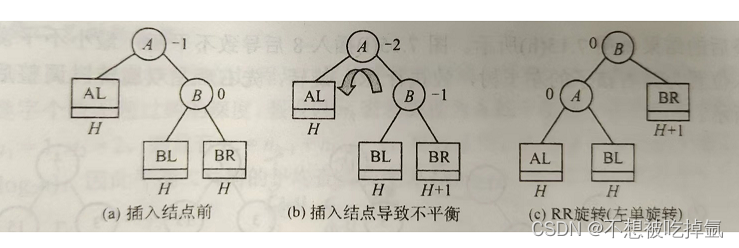
void rotateL(Node* parent) {Node* cur = parent->_right;Node* cur_left = cur->_left;parent->_right = cur_left;if(cur_left!=nullptr)cur_left->_parent = parent;cur->_left = parent;Node* ppNode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = cur;}else{ppNode->_right = cur;}cur->_parent = ppNode;}parent->_bf = 0;cur->_bf = 0;
}

先左后右双旋:

条件是 if(parent->_bf==-2&&cur->_bf==-1)

结构图如下： 注意H==0时，H-1=0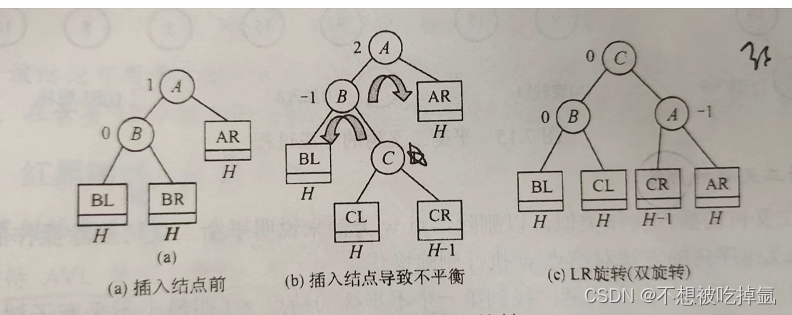

void rotateLR(Node* parent) {Node* cur = parent->_left;Node* cur_right = cur->_right;int bf = cur_right->_bf;//根据此节点的平衡因子决定，上层三个参加旋转的结点的平衡因子rotateL(parent->_left);//对平衡因子==±1的结点，即上层堆栈的cur，作为单左旋的parent，旋转后转为，单右旋的情况，再单右旋。rotateR(parent);if (bf == 1) {parent->_bf = 0;cur->_bf = -1;cur_right = 0;}else if (bf == -1) {parent->_bf = -1;cur->_bf =0;cur_right->_bf = 0;}else if (bf == 0) {parent->_bf = 0;cur->_bf = 0;cur_right->_bf = 0;}else {assert(false);}
}

先右后左双旋:

条件是：if(parent->_bf==2&&parent->_bf==-1)

结构图如下： 注意H==0时，H-1=0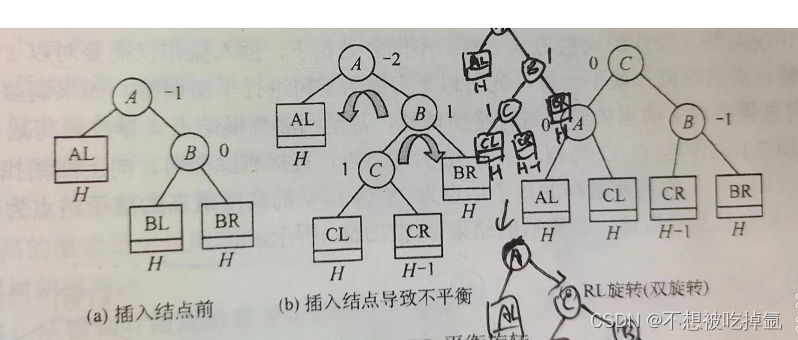

	void rotateRL(Node* parent) {Node* cur = parent->_right;Node* cur_left = cur->_left;int bf = cur_left->_bf;rotateR(parent->_right);rotateL(parent);if (bf == -1) {parent->_bf = 0;cur->_bf = 1;cur_left->_bf = 0;}else if (bf == 1) {parent->_bf = -1;cur->_bf = 0;cur_left->_bf = 0;}else if (bf == 0) {//当cur_left的子节点为空时，bf=0,parent->_bf = 0;cur->_bf = 0;cur_left->_bf = 0;}else {assert(false);}}