哈夫曼树

        在许多应用中，树中结点常常被赋予一个表示某种意义的数值，称为该结点的权。从树的根到任意结点的路径长度(经过的边数)与该结点上权值的乘积，称为该结点的带权路径长度。树中所有叶结点的带权路径长度之和称为该树的带权路径长度，记为：

        在含有n个带权叶结点的二叉树中，其中带权路径长度(WPL)最小的二叉树称为哈夫曼树，也称最优二叉树。例如，下图中的3棵二叉树都有4个叶子结点a, b,c,d,分别带权7,5,2,4，它们的带权路径长度分别为

                ​​​​​​​        

a. WPL = 7x2 + 5x2 + 2x2 + 4x2 = 36。
b. WPL = 4x2 + 7x3 + 5x3 + 2x1 = 46。
c. WPL = 7x1 + 5x2 + 2x3 + 4x3 = 35。
其中，图c树的WPL最小。可以验证，它恰好为哈夫曼树。

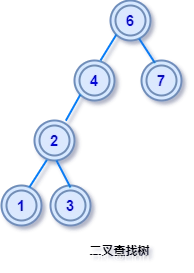
二叉查找树

        简单来说就是二叉树上所有节点的，左子树上的节点都小于根节点，右子树上所有节点的值都大于根节点。

                                        ​​​​​​​        ​​​​​​​       

平衡二叉查找树（AVL）

        在二叉查找树中，任一节点对应的两棵子树的最大高度差为 1，这样的二叉查找树称为平衡二叉树。其中左右子树的高度差也有个专业的叫法：平衡因子。

                                                        

AVL树的旋转

一旦由于插入或删除导致左右子树的高度差大于1，此时就需要旋转某些节点调整树高度，使其再次达到平衡状态，这个过程称为旋转再平衡。

     ​​​​​​​

        保持树平衡的目的是可以控制查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log n)，相比普通二叉树最坏情况的时间复杂度是 O(n) ，AVL树把最坏情况的复杂度控制在可接受范围，非常合适对算法执行时间敏感类的应用。

红黑树

        红黑树也是一种特殊的「二叉查找树」。到目前为止我们学习的 AVL 树和即将学习的红黑树都是二叉查找树的变体，可见二叉查找树真的是非常重要基础二叉树，如果忘了它的定义可以先回头看看。

        红黑树中每个结点都被标记了红黑属性，红黑树除了有普通的「二叉查找树」特性之外，还有以下的特征：

        节点是红色或黑色。根是黑色。所有叶子都是黑色（叶子是NIL节点）。每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。这些性质有兴趣可以自行研究，不过，现在你只需要知道，这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。

        ​​​​​​​        ​​​​​​​        

        而节点的路径长度决定着对节点的查询效率，这样我们确保了，最坏情况下的查找、插入、删除操作的时间复杂度不超过O(log n)，并且有较高的插入和删除效率。

红黑树 VS 平衡二叉树（AVL树）

        插入和删除操作，一般认为红黑树的删除和插入会比 AVL 树更快。因为，红黑树不像 AVL 树那样严格的要求平衡因子小于等于1，这就减少了为了达到平衡而进行的旋转操作次数，可以说是牺牲严格平衡性来换取更快的插入和删除时间。

        红黑树不要求有不严格的平衡性控制，但是红黑树的特点，使得任何不平衡都会在三次旋转之内解决。而 AVL 树如果不平衡，并不会控制旋转操作次数，旋转直到平衡为止。

        查找操作，AVL树的效率更高。因为 AVL 树设计比红黑树更加平衡，不会出现平衡因子超过 1 的情况，减少了树的平均搜索长度。

B树

B+树