进制算法题（进制转换、Alice和Bob的爱恨情仇）

进制的本质

对于一个十进制数字，比如说153，其本质是每一个数位上的数字乘上这一位上的权重，即:153=(1x $10^{2}$ )+(5x $10^{^{1}}$ )+(3 x $10^{0}$ )而二进制，只不过是把10换成了2，任意一个非负整数都有唯一的一个二进制表示:
$153_{10}$ = $(10011001)_{2}$
在计算机中，数字均通过二进制补码表示，所以学习进制转换尤为重要。

将任意进制转换为十进制

假设给了一个数组来表示一个k进制(假设K>10)的整数，我们该如何得到它的十进制数?

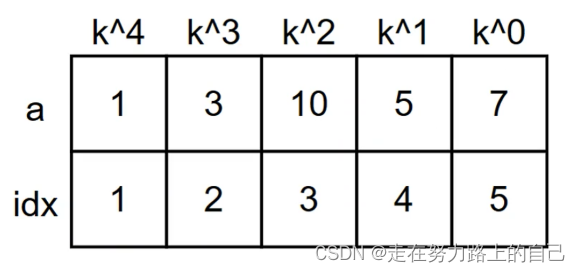
i = 1， $[ x = 1 \times k^0 ]$

i = 2， $[ x = 1 \times k^1 + 3 \times k^0 ]$

i =3， $[ x = 1 \times k^2 + 3 \times k^1 + 10 \times k^0 ]$

ll x = 0;
for (int i = 1; i <= n; ++i)
{x = x * k + a[i];
}
cout << x << '\n';

一般来说，这个k进制的数组可以通过对输入字符串的处理得到。

ll x; cin >> x;
while (x)a[++cnt] = x % k, x /= k;
reverse(a + 1, a + 1 + cnt);

例如十进制的11转换为二进制，根据这个规则得到的a数组为[1,1,0,1]，而实际上11的二进制为[1,0,1,1]。

一、进制

问题描述
请问十六进制数 2021ABCD 对应的十进制是多少?
答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

解题思路

从右至左给每一位编号，最右边为第0位，依次为第1位、第2位……对于“2021abcd”，d是第0位，c是第1位，依此类推。
每一位上的数字乘以16的相应次方（权重）。例如，d（十进制值）乘以16^0，c乘以16^1，b乘以16^2，a乘以16^3，1乘以16^4，2乘以16^5，0乘以16^6（注意这里的0不影响结果），2乘以16^7。
将步骤2中得到的所有乘积相加，得到最终的十进制值。

二、进制转换

用户登录

题目描述
给定一个 N 进制数 S，请你将它转换为 M 进制。
输入描述
第一行为一个整数 T，表示测试数据数量。(1 ≤ T < 10°)每个测试用例包含两行，第一行包含两个整数 N，M第二行输入一个字符串 S，表示 N 进制数。
数据范围保证:2<N,M<16，若N >10，则用 A~ F 表示字码10 ~ 15。保证 S 对应的十进制数的位数不超过 10。
输出描述
输出共 T，每行表示一组数据的答案

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1001;
int a[N];
char ch[] = { '0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F' };void solve() {int n, m; cin >> n >> m;// 输入 n, m// n 表示 输入的n进制, m表示 需要输出 m进制string s; cin >> s;// 输入字符串int len = s.length();//获取字符串长度s = "#" + s; // 其他字符也行, 不是一定要 "#"// 在前面添加一个"#"字符，这是为了让字符串的索引从1开始，以方便处理。for (int i = 1; i <= len; ++i) {if ('0' <= s[i] && s[i] <= '9') { // 如果字符属于 0~9a[i] = s[i] - '0'; // 将字符直接转换为数字  }else { //如果属于大学字母a[i] = s[i] - 'A' + 10; // 将大写字母转换为数字（A=10, B=11, ...）  }}ll x = 0;for (int i = 1; i <= len; ++i) {x = x * n + a[i]; // 通过遍历数组a，将原始进制下的数转换为十进制数值x}string ans;// 将十进制数值 x转换为m进制的字符串表示answhile (x) {ans += ch[x % m];  x /= m;// 使用ch数组来找到每一位的字符表示，// 并通过不断除以目标进制m来获取下一个字符，直到x变为0}reverse(ans.begin(), ans.end());// 反转字符串以得到正确的顺序（如果需要的话）  cout << ans << '\n';  
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int T; cin >> T;// 输入一个整数 T, 表示测试数据数量while (T--)solve();// 多组数据输入return 0;
}

三、Alice和Bob的爱恨情仇

用户登录

问题描述

Bob和Alice通过博弈的方式来吃掉小饼干。他们将小饼干分成n堆，每堆有αi个小饼干。他们轮流对这些饼干进行操作，每次从一堆中拿出k^m个小饼干（k为奇数且m≥0，且km不能超出该堆的总数）。当一方操作后没有剩余的小饼干，则该方获胜。Alice先手，两人都会以最佳方法取饼干。请问谁能赢？

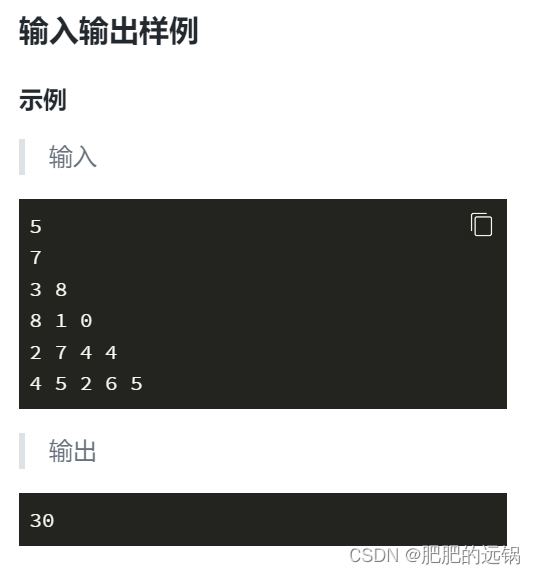
输入格式

第一行：两个正整数n（1≤n≤2×10^5）和k（1≤k≤10^9），分别表示饼干的堆数和每次取出饼干的底数。
第二行：n个整数，第i个表示第i堆小饼干有αi（1≤αi≤10^6）个小饼干。
输出格式

输出一行，包含一个字符串，表示Alice和Bob之中获胜的那个人。

诈骗题。
注意到 k 为奇数，而且每次至少可以取走一个石子。这意味着实际上
k^m 毫无意义，只与那一堆石子的奇偶数有关。更进一步，只与所有石
子堆的石子数之和的奇偶有关，若是奇数，则 Alice 胜，否则 Bob 胜。
时间复杂度 O(n)。

解题思路

k 是奇数
当 k 是奇数时，每次可以取走 (k^m) 个小饼干（m 是非负整数），由于 (k^m) 总是奇数（奇数的任何非负整数次幂都是奇数），因此：

如果一开始有 x 个小饼干，且 x 是奇数，那么先手总是可以取走 (k^m) 个小饼干，使得剩下的小饼干数量是偶数。然后无论后手如何取，先手总是可以取走 1 个小饼干，保持剩余小饼干数量为偶数。最终，先手将取走最后一个小饼干，赢得游戏。
如果一开始有 x 个小饼干，且 x 是偶数，那么无论先手如何取，后手总是可以取走 1 个小饼干，使得剩余小饼干数量为奇数。然后先手无论如何取，后手都可以取走 (k^m) 个小饼干，保持剩余小饼干数量为奇数。最终，后手将取走最后一个小饼干，赢得游戏。

在这道题中，题目还特别强调了 k 是奇数，由此我们可以进行大胆的推测这个博弈的结果跟奇偶数有很大关系。由于每次取值都是 k 的幂次方，由于 k 是奇数，故每次取的数也将是奇数。

总结：

在一个奇数堆中，由于每次取不超过总数的奇数个数的饼干，所以我们到最后取完的时候一定会取奇数次，同理可得，在一个偶数堆中则是取偶数次。

故可知对于 (1,2,…,)(a1,a2,…,an) 会有所对应的 (1,2,…,)(b1,b2,…,bn) ,其中 bi == ( ai % 22 ) ，当 bi 为 1 时代表取奇数， bi 为 0 时代表取偶数。

由此可得出 ans= (1,2,…)(b1,b2,…,bn) % 2，其中 ans 为 1 时代表总取数为奇数，即 Alice 赢，ans 为 0 时代表总取数为偶数，即 Bob 赢。

#include <bits/stdc++.h>void solve(const int &Case) {int n, k;std::cin >> n >> k;int ans = 0;for (int i = 0; i < n; i++) {int x;std::cin >> x;ans ^= x & 1;}if (ans > 0)std::cout << "Alice\n";else std::cout << "Bob\n";
}int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int T = 1;for (int i = 1; i <= T; i++)solve(i);return 0;
}

或者：

#include <iostream>
using namespace std;
long long ans,n,k,x;
int main()
{cin>>n>>k;while(n--){cin>>x;ans+=(x%2); }if(ans%2){cout<<"Alice";}else{cout<<"bob";}return 0;
}

今天就先到这了！！！