---

前言

之前我们已经完全弄明白了中心损失函数里的代码是什么意思，并且怎么用的了，现在我们来运行它。

论文：https://ydwen.github.io/papers/WenECCV16.pdf
github代码：https://github.com/KaiyangZhou/pytorch-center-loss

前文：【center-loss 中心损失函数】 原理及程序解释（完）

简单总结一下

这段主代码，还是先以小见大。

首先，有很多点，以普通的拟合直线为例子，假设直线是用来做分类问题，一条直线分成两类，或者说是回归问题，则就是，每个点落在两类的例子是多少。（可以想象可以用来做很多事。）
我们是这样一步一步做的
1、确立损失函数（作为评判好的模型的标准）。（损失函数有很多可选，具体使用具体分析）
2、随机设置权重参数（作为最后好的模型的参数）。(随机函数也有很多可选)
3、确立模型（如：y=wx+b）
4、计算当前的参数得出的值与实际值（标签值）的误差（可跳，损失函数里一般有此值），后代入（1）中的损失函数求得损失值。
5、确定降低损失值的方法。（有梯度下降法或数学公式法）注意这里是对损失函数求导！！！
6、得出由方法计算出的参数值。

贴一下：（梯度下降法的代码）

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt# 生成模拟数据，假设真实的w为2，b为3
np.random.seed(0) # 设置随机种子
x = np.linspace(0, 10, 100) # 生成100个在[0,10]的等距数 (包括0，10)
y = 2 * x + 3 + np.random.normal(0, 1, 100) # 生成y值，加入噪声# 定义一元线性回归模型
def linear_regression(x, w, b):return w * x + b# 定义均方误差函数
def mean_squared_error(y_true, y_pred):return np.mean((y_true - y_pred) ** 2)# 定义梯度下降算法
def gradient_descent(x, y, w, b, lr, epochs):# x: 自变量# y: 目标变量# w: 斜率的初始值# b: 截距的初始值# lr: 学习率# epochs: 迭代次数n = len(x) # 样本数量history_w = [] # 用来记录w的历史值history_b = [] # 用来记录b的历史值history_loss = [] # 用来记录损失函数的历史值for i in range(epochs): # 迭代epochs次# 计算预测值y_pred = linear_regression(x, w, b)# 计算损失值loss = mean_squared_error(y, y_pred)# 计算梯度dw = -2/n * np.sum((y - y_pred) * x)db = -2/n * np.sum(y - y_pred)# 更新w和bw = w - lr * dwb = b - lr * db# 记录w，b和损失值history_w.append(w)history_b.append(b)history_loss.append(loss)# 打印结果print(f"Epoch {i+1}: w={w:.4f}, b={b:.4f}, loss={loss:.4f}")return history_w, history_b, history_loss# 设置超参数
w = 0 # 斜率的初始值
b = 0 # 截距的初始值
lr = 0.02 # 学习率
epochs = 200 # 迭代次数# 调用梯度下降算法
history_w, history_b, history_loss = gradient_descent(x, y, w, b, lr, epochs)# 绘制损失函数的变化曲线
plt.plot(range(epochs), history_loss, color="r")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Loss Curve")
plt.show()# 绘制最终的拟合直线
plt.scatter(x, y, color="b", label="Data")
plt.plot(x, linear_regression(x, history_w[-1], history_b[-1]), color="g", label="Fitted Line")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Linear Regression")
plt.legend()
plt.show()

这里我们神经网络逻辑上还是一样。
1、确立损失函数 多了中心损失函数
2、随机设置权重参数nn.parameters()
3、确立模型这里用了CNN模型
4、求得损失值
5、确定降低损失值的方法这里也是梯度下降法
6、得出参数值

原来神经网路并没有想象中的那么高深，只是在原来基础上，做了很多的优化。
贴一下：（简单线性层的模型）

import torch
import torch.nn as nn
import torch.optim as optim#设置随机种子
torch.manual_seed(0)
# 生成一些随机的输入和标签
x = torch.randn(100, 1) # 100个样本，每个样本有1个特征  randn
y = 3 * x + 5 + torch.randn(100, 1) # 100个样本，每个样本有1个标签，服从 y = 3x + 5 + 噪声 的分布# 定义一个简单的线性模型
model = nn.Linear(1, 1) # 输入维度是1，输出维度是1
# 定义一个均方误差损失函数
criterion = nn.MSELoss()
# 定义一个随机梯度下降优化器
optimizer = optim.SGD(model.parameters(), lr=0.01) # 学习率是0.01# 训练100个迭代
for epoch in range(100):# 清零梯度optimizer.zero_grad()# 得到预测结果output = model(x)# 计算损失loss = criterion(output, y)# 反向传播，计算梯度loss.backward()# 更新参数optimizer.step()# 打印损失print(f"Epoch {epoch}, loss {loss.item():.4f}")# 打印模型参数
print(model.weight)
print(model.bias)

参数对比

之前我们第一个代码与第二个用到的参数：
w:权重
b:偏置
lr:学习率，乘在梯度前
epoch:迭代次数

此github代码：
model.parameters():里面为W权重矩阵、b偏置
criterion_cent.parameters():里面为W权重矩阵、b偏置
lr:学习率，乘在梯度前 这里lr_model为0.001，lr_cent为0.5
epoch:迭代次数 这里为100
变化
weight_decay：权重衰减（=L2惩罚项），一般很小 ，防止过拟合 一般5e-4 这里为5e-4
momentum：动量，乘在速度项前，用来加速学习过程 一般0.5-0.9 这里为0.9
gamma：学习率下降,乘在学习率前，一般0-1之间 这里为0.5
stepsize：学习率下降周期，每隔多少stepsize下降一次 这里为20

torch.optim.SGD(params, lr=0.001, momentum=0, dampening=0, weight_decay=0, nesterov=False, *, maximize=False, foreach=None, differentiable=False)

未用到的默认参数：
nesterov：使用Nesterov动量方法，默认为False。
maximize：梯度找山顶，默认为False。
foreach：None时，在使用Cuda的情况下性能会更好，默认为None。
differentiable:选择为True时，可能会损害性能，默认为False。

解释参数

还是用官方SGD的图来解释一下更新的代码。
已知y(学习率)，θ0（参数），f(θ)（目标损失函数），λ（权重衰减），μ（动量），τ（阻尼）
默认θ0为随机值，b1为0。(bt为中间量，或者叫动量缓冲区。累积了之前的梯度信息）

第一次迭代t=1时，求损失函数的梯度赋给g1,
如果权重衰减λ不为0，则g1 = g1 + λθ0。

以下讲解这行代码：

权重衰减（L2正则化）

这里在梯度中加入了权重参数θ0的信息，从而提高模型泛化的能力。

这个参数λ之所以很小，是因为我们不希望正则化项主导整个损失函数，而只是作为一个轻微的调整。

这个惩罚项会鼓励模型学习到更小的权重，因为大的权重会导致惩罚项增大，从而增加整体的损失函数值。

所以，当我们更新权重时，实际上是在原始梯度的基础上加上了这个惩罚项的梯度。这样做可以防止权重变得过大，有助于防止模型过拟合。

原理参考：机器学习中，L2正则化的原理，及其可以防止过拟合的原因

公式：

其中：L2范数为

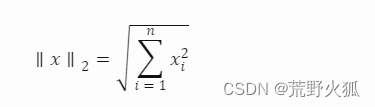
这里是在损失函数环节上加的L2正则化。

这里解释下上文：g1 = g1 + λθ0
1、这里不是θ0 ²,原因其实就是上面一步求梯度，已经将平方项移下来了（当然也有可能损失函数没有平方项）。
或者，我们可以看成，梯度项相加时，我们也要对 λ·IIwII² 求导，此时的平方项2就下来了，放进超参数里了。

2、至于L2范数里的求和为什么在g1 = g1 + λθ0 里没写，解释：是有这个操作的，只是求gt里也没写求和的操作，那为简便写伪代码起见，就也没写。

继续：

动量

如果动量u为0，则直接进行判断是否是求梯度最小还是梯度最大，如果最大则θ1 = θ0 + y x g1 ,如果最小则是θ1 = θ0 - y x g1 。

如果动量u不为0，此时判断t=1,则b1 = g1,
如果使用Nesterov动量方法，则g1 = g1 + ub1 (实际上是g1 =（1+u）x g1)，如果不使用则g1 = b1。(可以看出Nesterov动量方法相比于原方法收敛更快)

然后如上更新。

t =2时，(λ、u不为0的情况 )损失函数求导得出g2-> g2 = g2+λθ1
此时判断t>1, 则b2 = ub1 +（1-τ）x g2 (此时b1 = g1) 可以看出当τ为0时，动量u起到一个加速作用

-> 之后同上。

momentum动量解释：
是用来加速梯度下降过程的，但如果动量值设置大于1，会导致更新步长过大，从而可能导致优化过程在最小值附近震荡，甚至发散，而不是收敛到最小值。动量的目的是为了帮助梯度下降算法更快地穿过平坦区域并减少震荡，但它也需要保证整个过程的稳定性。

dampening阻尼解释：
“dampening” 通常指的是减少振荡和过度调整的过程。在随机梯度下降（SGD）中，当使用动量（momentum）时，dampening 参数用于减少动量的影响，从而帮助稳定学习过程。如果设置为非零值，dampening 会减少累积过去梯度的速度，这样可以防止在最小值附近的过度震荡。

例如，在PyTorch的 torch.optim.SGD 优化器中，dampening 参数通常与动量一起使用。如果不希望使用动量的衰减效果，可以将 dampening 设置为0。如果设置了 dampening，每次更新时累积的动量会乘以 (1 - dampening )。这样，即使动量保持不变，通过调整 dampening，也可以控制优化过程的平滑程度。

其他参数

# argparse.ArgumentParser() 创建一个ArgumentParser对象 用来处理命令行参数
parser = argparse.ArgumentParser("Center Loss Example")
# dataset # 数据集
# add_argument() 方法用于指定程序需要接受的命令参数
parser.add_argument('-d', '--dataset', type=str, default='mnist', choices=['mnist']) # 选择数据集 例：python main.py -d mnist
parser.add_argument('-j', '--workers', default=4, type=int,help="number of data loading workers (default: 4)") # 数据加载工作线程数 例：python main.py -j 4 #-j表示短名称
# optimization # 优化
parser.add_argument('--batch-size', type=int, default=128) # 批大小
parser.add_argument('--lr-model', type=float, default=0.001, help="learning rate for model") # 学习率
parser.add_argument('--lr-cent', type=float, default=0.5, help="learning rate for center loss") # 中心损失学习率
parser.add_argument('--weight-cent', type=float, default=1, help="weight for center loss") # 中心损失权重
parser.add_argument('--max-epoch', type=int, default=100) # 最大迭代次数
parser.add_argument('--stepsize', type=int, default=20) # 学习率下降间隔 : 每隔多少个epoch下降一次
parser.add_argument('--gamma', type=float, default=0.5, help="learning rate decay") # 学习率衰减 : 学习率下降的倍数 比如0.5表示学习率减半
# model # 模型
parser.add_argument('--model', type=str, default='cnn') # 模型选择
# misc # 其他
parser.add_argument('--eval-freq', type=int, default=10) # 评估频率
parser.add_argument('--print-freq', type=int, default=50) # 打印频率 
parser.add_argument('--gpu', type=str, default='0') # GPU
parser.add_argument('--seed', type=int, default=1) # 随机种子
parser.add_argument('--use-cpu', action='store_true') # 是否使用CPU action='store_true' 表示如果有这个参数则为True
parser.add_argument('--save-dir', type=str, default='log') # 保存路径 保存训练日志 保存在log文件夹下
parser.add_argument('--plot', action='store_true', help="whether to plot features for every epoch") # 是否绘制特征图args = parser.parse_args() # 解析参数 保存到args中

运行

进入colab官网白嫖gpu。
参考：利用谷歌colab跑github代码详细步骤

$ git clone https://github.com/KaiyangZhou/pytorch-center-loss
$ cd pytorch-center-loss
$ python main.py --eval-freq 1 --gpu 0 --save-dir log/ --plot

评估频率1epoch1次， gpu选择0号。保存在log文件夹下并绘图。
运行如下：

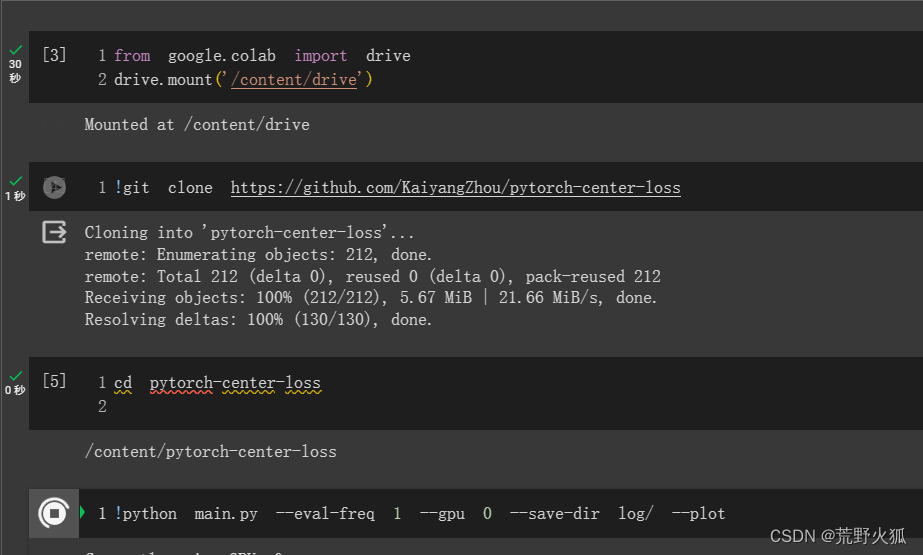
运行截图如下：

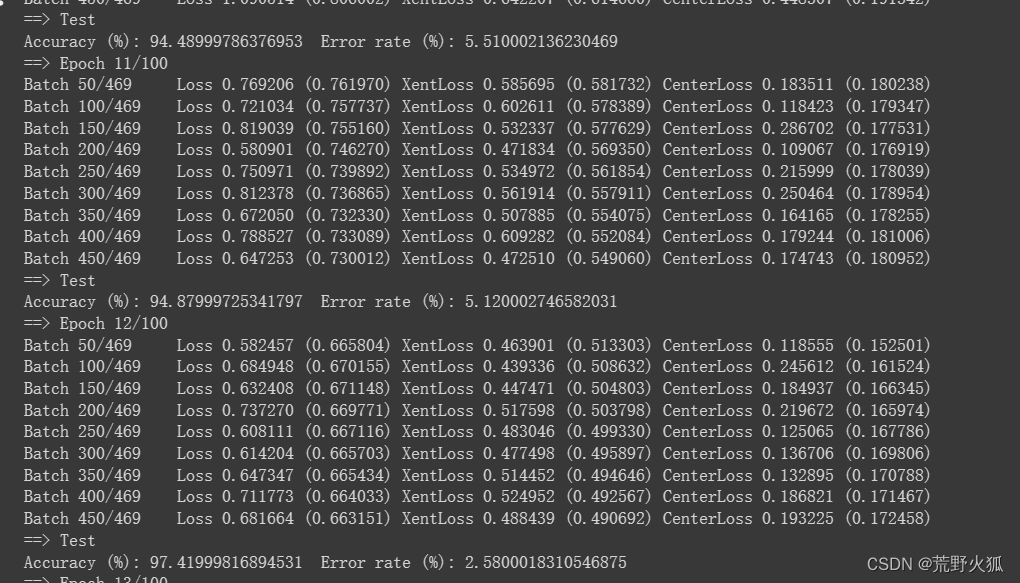
发现在第12epoch时就达到了97%的正确率。

在第32epoch时就基本上达到了高峰，然后逐渐下降。

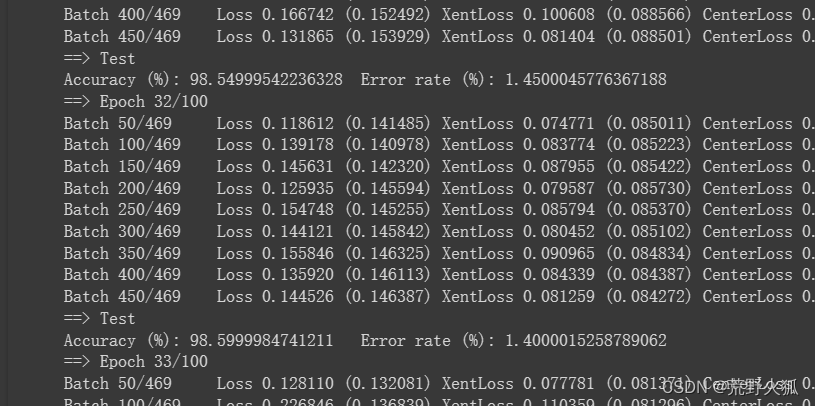
如预期所见生成了log的文件夹。

选择train/epoch_33.png 如下：

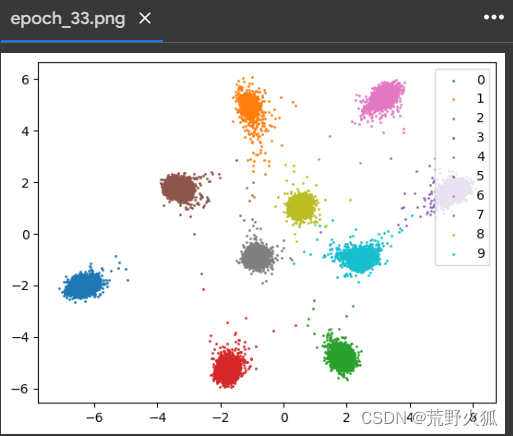
分离表现的还不错。