【数据结构】栈和队列的应用——括号匹配 + 表达式求值 + 表达式转换 +栈的递归应用+队列在计算机系统中的应用

文章目录

- 3.栈的应用
- - 3.1 括号匹配问题
  - 3.2 表达式求值
  - - 3.2.1 三种算术表达式
    - 3.2.2 后缀表达式
    - - A.中缀转后缀
      - B.后缀表达式的计算
    - 3.2.3 前缀表达式
    - - A.中缀转前缀
      - B.前缀表达式的计算
    - 3.2.4 中缀表达式的求值
  - 3.3 递归中栈的应用
- 4.队列的应用

栈基础知识：【数据结构】栈顺序栈链栈（共享栈创建进栈出栈读取）完整代码+解析
队列基础知识：【数据结构】队列循环队列双端队列——顺序队列+链式队列完整代码

3.栈的应用

3.1 括号匹配问题

问题阐述
判断一组有()[]{}这些括号的字符串，判断左右括号是否匹配。
- 括号需要从里向外一层层匹配，符合栈后进先出的特点，所以用栈解决括号匹配问题。
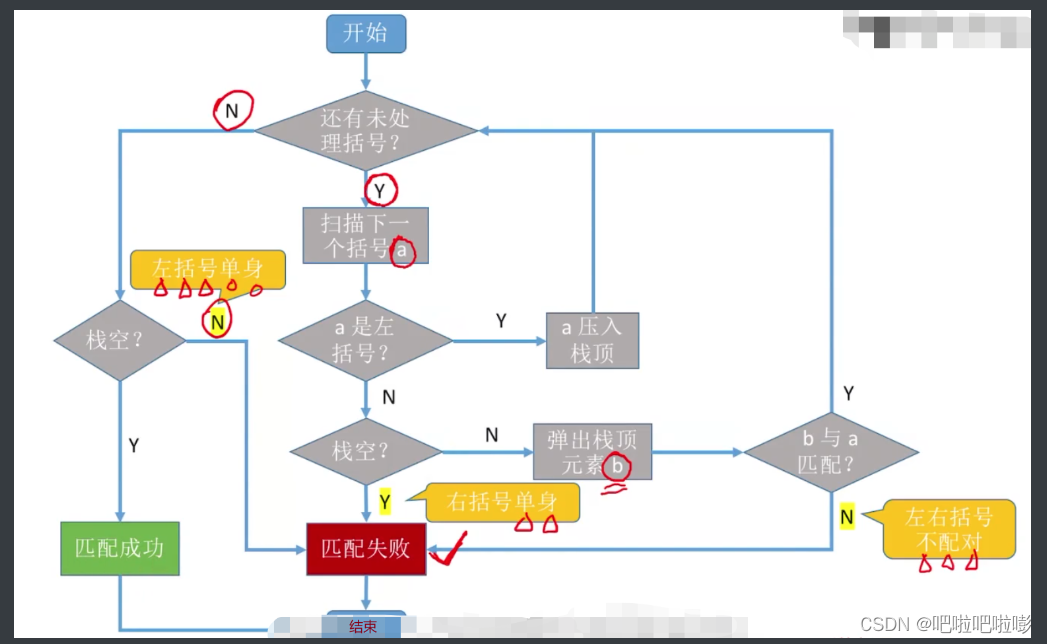
匹配流程：
算法流程：

1.创建空栈，顺序遍历括号；

2.若是左括号，压入栈中，继续扫描；

3.若是右括号，弹出栈顶元素，判断两个括号类型是否匹配；

4.遍历完后判断栈是否空。

#include<stdio.h>
#include<stdlib.h>#define ElemType char 
#define MaxSize 9typedef struct {ElemType data[MaxSize];int top;
}SqStack;void InitStack(SqStack& Q) {Q.top = -1;
}bool isEmpty(SqStack& Q) {if (Q.top == -1)return true;elsereturn false;
}bool Push(SqStack& Q, ElemType x) {if (Q.top + 1 == MaxSize)return false;Q.data[++Q.top] = x;return true;
}bool Pop(SqStack& Q, ElemType& x) {if (Q.top == -1)return false;x = Q.data[Q.top--];return true;
}//括号匹配算法
bool bracketCheck(char s[],int length) {SqStack Q;InitStack(Q);char topElem;for (int i = 0; i < length; i++) {if (s[i] == '(' || s[i] == '[' || s[i] == '{') {Push(Q, s[i]);}else {Pop(Q, topElem);if (s[i] == ')' && topElem == '(' || s[i] == ']' && topElem == '[' || s[i] == '}' && topElem == '{')continue;elsereturn false;}}if (!isEmpty(Q))return false;return true;
}int main() {char s1[6] = { '(','(','[',']',')' };char s2[4] = { '(','{',']' };char s3[7] = { '(','[','{','}',']',')'};printf("%d\n",bracketCheck(s1, 5));printf("%d\n", bracketCheck(s2, 3));printf("%d\n", bracketCheck(s3, 6));
}

3.2 表达式求值

3.2.1 三种算术表达式

中缀表达式
就是我们日常所用的表达式。

由操作符、界限符、操作数组成。
- 运算符在两个操作数中间。
后缀表达式（逆波兰式）

运算符在两个操作数后面。
前缀表达式（波兰式）

运算符在两个操作数前面。

3.2.2 后缀表达式

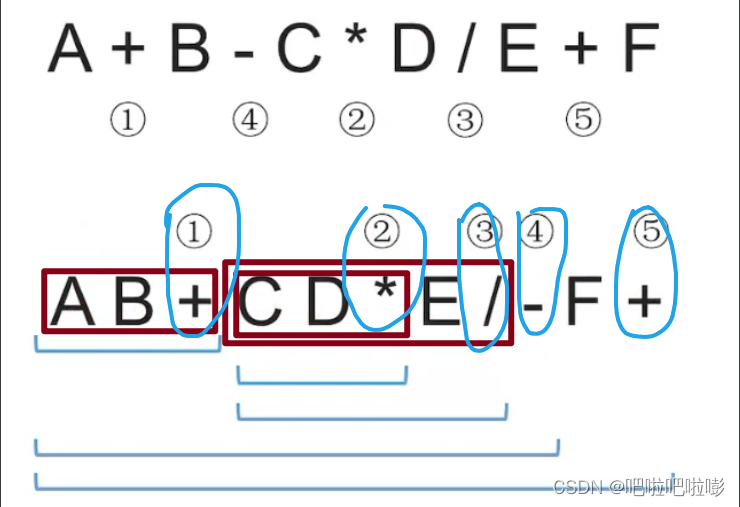
A.中缀转后缀

手算方法
1.确定中缀表达式中各运算符的运算顺序。

2.选择下一个运算符，按**【左操作数右操作数运算符】方式组合成新的操作数**。

3.如果还有运算符没被处理，就继续第2步。
- 注：运算顺序不唯一，对应的后缀表达式也不唯一，但机算是左优先原则。
- 左优先原则：只要左边的运算符能先计算，就优先算左边。（可确保运算顺序唯一）
机算
初始化一个栈（用于保存暂时不能确定运算顺序的运算符）

从左往右处理各元素，直到末尾，可能遇到以下三种情况：
- 1.遇到操作数。
  
  直接加入后缀表达式；
- 2.遇到界限符。
  
  遇到‘（’直接入栈；
  
  遇到‘）’依次弹出栈内运算符并加入后缀表达式，直到弹出‘（’；
- 3.遇到运算符。
  
  依次弹出栈中优先级高于或等于当前运算符的所有运算符，加入后缀表达式，
  
  若碰到‘（’或栈空停止，
  
  再把当前运算符入栈。

中缀转后缀完整代码

#include<stdio.h>
#include<string.h>#define ElemType char
#define MaxSize 99typedef struct {ElemType data[MaxSize];int top;
}SqStack;void InitStack(SqStack& Q) {Q.top = -1;
}bool isEmpty(SqStack& Q) {if (Q.top == -1)return true;elsereturn false;
}bool Push(SqStack& Q, ElemType x) {if (Q.top + 1 >= MaxSize)return false;Q.data[++Q.top] = x;return true;
}bool Pop(SqStack& Q, ElemType& x) {if (Q.top == -1)return false;x=Q.data[Q.top--];return true;
}//运算符优先级判断
int Priority(char x) {if (x == '-' || x == '+')return 1;else if (x == '*' || x == '/')return 2;else if (x == '(') return 0;return -1; 
}//中缀转后缀
//in是待转换的中缀表达式，suf是转换后的前缀表达式
void in2suf(char in[], char suf[]) {//初始化一个栈SqStack Q;InitStack(Q);int isuf = 0;//suf数组下标char x;//从左往右遍历各元素for (int i = 0; i < strlen(in); i++) {if (in[i] >= '0' && in[i] <= '9') //遇到操作数。{suf[isuf++] = in[i]; //直接加入后缀表达式}else if (in[i] == '(') //遇到‘（’{Push(Q, in[i]); //直接入栈}else if (in[i] == ')')  //遇到‘）’{Pop(Q, x); //依次弹出栈内运算符while (x != '(') {suf[isuf++] = x; //并加入后缀表达式Pop(Q, x);}	}else //遇到运算符{ //依次弹出栈中优先级高于或等于当前运算符的所有运算符while (!isEmpty(Q)&&Priority(in[i]) <= Priority(Q.data[Q.top])) {if (Q.data[Q.top] == '(')break; //若碰到‘（’或栈空停止Pop(Q, x);suf[isuf++] = x; //加入后缀表达式}Push(Q, in[i]); //当前运算符入栈}}while (!isEmpty(Q)){Pop(Q, x);suf[isuf++] = x;}suf[isuf] = '\0';
}int main() {char in[] = "1+5*(2+3)/(4-2)+3*1";char suf[MaxSize];in2suf(in, suf);printf("%s\n", in);printf("%s\n\n", suf);return 0;
}

在这里插入图片描述

B.后缀表达式的计算

手算

从左往右扫描，遇到一个运算符，就让运算符前面最近的两个操作数执行对应运算，合并为一个操作数。
机算

用栈实现后缀表达式的计算：

1.从左往右扫描下一个元素，直到处理完所有元素；

2.若扫描到操作数则压入栈，并返回第1步，否则执行第3步；

3.若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到第1步。

后缀表达式求值完整代码

#define  _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>#define ElemType int
#define MaxSize 99typedef struct {ElemType data[MaxSize];int top;
}SqStack;void InitStack(SqStack& Q) {Q.top = -1;
}bool isEmpty(SqStack& Q) {if (Q.top == -1)return true;elsereturn false;
}bool Push(SqStack& Q, ElemType x) {if (Q.top + 1 >= MaxSize)return false;Q.data[++Q.top] = x;return true;
}bool Pop(SqStack& Q, ElemType& x) {if (Q.top == -1)return false;x = Q.data[Q.top--];return true;
}//后缀表达式求值
int Computed_suf(char suf[]) {SqStack Q;InitStack(Q);int a, b,c;//从左往右扫描下一个元素，直到处理完所有元素for (int i = 0; i < strlen(suf); i++) {if (suf[i] >= '0' && suf[i] <= '9') { //若扫描到操作数则压入栈Push(Q, suf[i]-'0');}else { //若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶Pop(Q, b);Pop(Q, a);if (suf[i] == '+') {c = a + b;}else if (suf[i] == '-') {c = a - b;}else if (suf[i] == '*') {c = a * b;}else if (suf[i] == '/') {c = a / b;}Push(Q, c);}}return Q.data[Q.top];
}int main() {char s[] = "1523+*72-/+31*+"; //1+5*(2+3)/(7-2)+3*1=9printf("%d", Computed_suf(s));return 0;
}

3.2.3 前缀表达式

A.中缀转前缀

手算
1.确定运算顺序；

2.选择下一个运算符，按【运算符左操作数右操作数】的方式组合成新操作数；

3.如果还有运算符没被处理，重复第2步。
- 右优先原则：只要右边运算符能先计算，就优先算右边。

B.前缀表达式的计算

用栈实现前缀表达式的计算：

1.从右往左扫描下一个元素，直到全部处理完；

2.若扫描到操作符则压入栈，返回第1步，否则执行第3步；

3.遇到运算符，弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，返回第1步。

注：在弹出的两个栈顶元素中，先出栈的是左操作数。

3.2.4 中缀表达式的求值

方法

用栈实现，就是中缀转后缀＋后缀表达式计算

1.初始化两个栈：操作数栈+运算符栈；

2.若扫描到运算符或界限符，则按中缀转后缀相同逻辑压入运算符栈

3.3 递归中栈的应用

函数调用特点

最后被调用的函数最先执行结束（LIFO）
调用函数时，需要用一个栈存储：

1.调用返回地址；

2.实参；

3.局部变量。
递归的精髓：
将原始问题转换为属性相同但规模较小的小问题。

大问题---->小问题
- 但通常情况下，递归能减少代码量但效率不高。
在计算机中，用栈来解决函数的递归调用
递归调用时，函数调用栈可称为“递归工作栈”，

每进入一层递归，就将递归调用所需信息压入栈，

每退出一层递归，就从栈顶弹出相应信息。
- 通俗的说：函数调用，就是函数入栈；函数得到值，就是栈的弹出；
- 缺点：递归太多可能导致栈溢出。