🚀个人主页：为梦而生~ 关注我一起学习吧！
💡专栏：算法题、 基础算法~赶紧来学算法吧
💡往期推荐：
【算法基础 & 数学】快速幂求逆元（逆元、扩展欧几里得定理、小费马定理）
【算法基础】深搜

---

---

1 引言

1.1 树状数组的概念

树状数组（Binary Indexed Tree，BIT）是一种数据结构，用于高效地处理数组的动态查询和更新操作。它可以在O(log n)的时间复杂度内完成单点更新和前缀和查询操作。树状数组常用于解决数组频繁更新和查询前缀和的问题，比如求解逆序对、区间和等。

1.2 树状数组的应用场景

1. 动态查询问题：树状数组非常适用于需要动态查询某个区间内元素和的场景。
2. 频繁更新问题：树状数组也适用于频繁更新数组元素的情况。
3. 逆序对问题：逆序对问题是一个常见问题，即找出数组中所有满足i<j且a[i]>a[j]的(i, j)对。树状数组可以在O(nlogn)的时间复杂度内解决这个问题。

---

2 基础知识

2.1 二进制索引的概念和性质

二进制索引，也称为树状数组或有限差分数组，是一种特殊的数据结构，用于高效地处理数组中的前缀和查询。它的核心思想是利用二进制表示中的每一位来快速计算前缀和，从而实现高效的查询和更新操作。

概念：

二进制索引的主要概念是基于数组元素的二进制表示来构建索引。具体来说，对于数组中的每个元素，我们可以将其下标转换为二进制形式，并根据二进制位来构建索引。通过维护这些索引，我们可以快速计算数组的前缀和，从而实现高效的查询和更新操作。

性质：

• 前缀和查询的高效性：二进制索引可以在O(log n)的时间复杂度内计算数组的前缀和。这是因为它利用了二进制表示的特性，通过跳跃式地计算不同位上的前缀和，实现了快速查询。
• 单点更新的高效性：与前缀和查询一样，二进制索引也可以在O(log n)的时间复杂度内完成单点更新操作。当数组中的某个元素发生变化时，只需要更新对应的索引，即可快速反映到前缀和上。
• 空间效率：二进制索引的空间复杂度与原始数组相同，即O(n)。它不需要额外的存储空间来维护索引结构，因此具有较高的空间效率。

2.2 前缀和的概念和计算

前缀和（Prefix Sum）是一个数组的概念，指的是数组中从第一个元素开始到某个位置元素（包括该位置元素）的总和。前缀和通常用于快速计算某个区间的和，避免了对每个元素进行逐一相加的操作，从而提高计算效率。

计算前缀和的方法很简单，通常是通过迭代数组中的每个元素，并将当前元素与前一个元素的前缀和相加，得到当前元素的前缀和。第一个元素的前缀和就是它本身。

例如，给定一个数组 arr = [1, 2, 3, 4, 5]，它的前缀和数组 prefix_sum 可以这样计算：

prefix_sum[0] = arr[0] = 1  
prefix_sum[1] = arr[0] + arr[1] = 1 + 2 = 3  
prefix_sum[2] = arr[0] + arr[1] + arr[2] = 1 + 2 + 3 = 6  
prefix_sum[3] = arr[0] + arr[1] + arr[2] + arr[3] = 1 + 2 + 3 + 4 = 10  
prefix_sum[4] = arr[0] + arr[1] + arr[2] + arr[3] + arr[4] = 1 + 2 + 3 + 4 + 5 = 15

所以，前缀和数组 prefix_sum 为 [1, 3, 6, 10, 15]。

---

3 树状数组的定义和数学推导

3.1 通俗易懂的解释什么是树状数组※

对于一个数组，我们通常需要这样的操作：

1. 修改某个元素的值
2. 求一段区间的和

如果用朴素的做法，我们通常需要开一个数组，保存下来所有元素，每查询一次，遍历一次数组

但这会使得求和操作的时间复杂度达到$O(n)$，但如果数据量和查询次数达到上百万，这样的效率太低了

• 但有人可能会想到，把数组中的元素两两求和，保存到另一个数组中：
  

这样我们在计算的时候就会节省一半的时间，修改数据的时候也就是多改一个数字而已，但是对于很大的数据量，还是很慢。

• 那我们可以再将这一层元素两两求和，往上叠加一层，直到只剩一个元素为止：
  

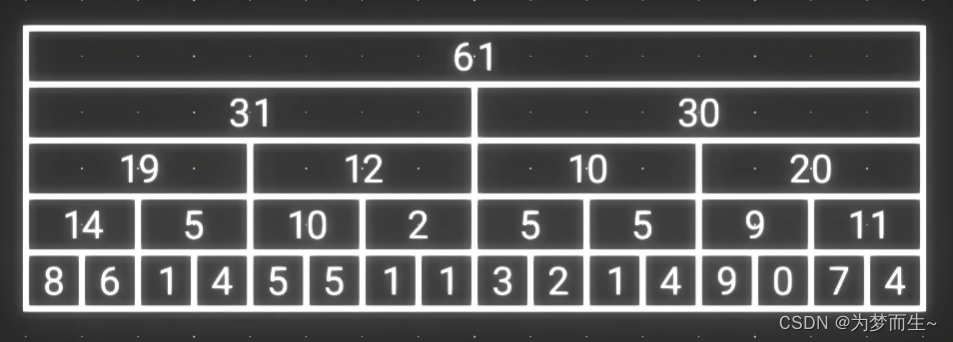
这样即使要求和的数字很多，我们也可以利用这些额外的数组计算出需要的答案（用空间换时间的思想）

例如：要计算前14个数字的和

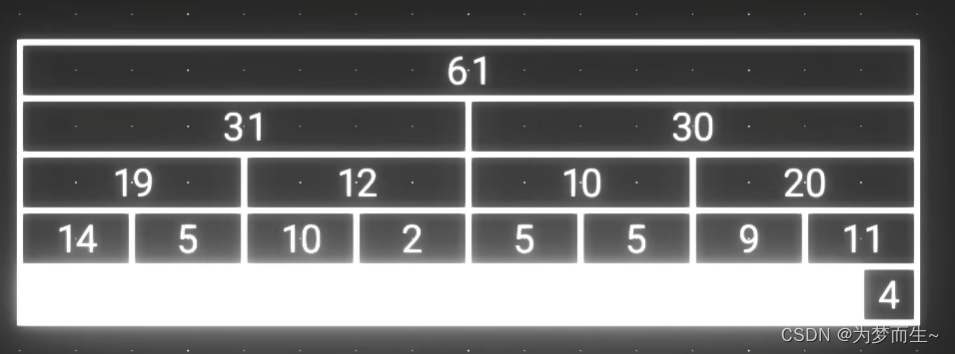
只需要计算这样4个数字就行

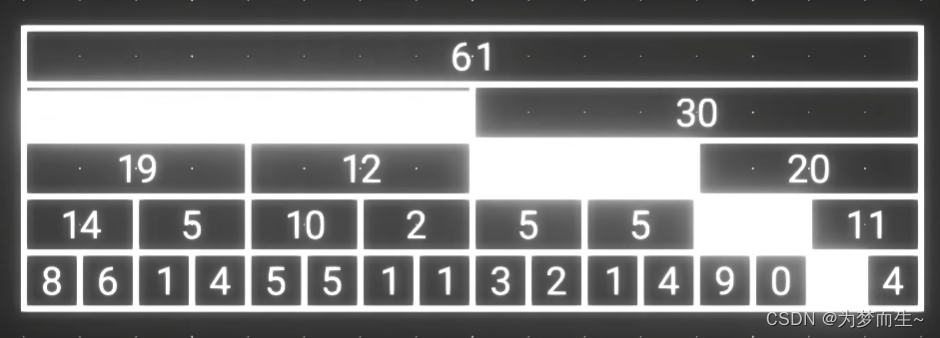
即使要计算前一百万个数字的和，我们也只需要进行10~20次加法

这样将查询的时间复杂度降到了$O(\log n)$，效率提升了很多

观察这个数组我们可以发现，数组中的某些数字是不会用到的，大家可以手动模拟一下，所有层的第偶数个数字在计算时都不会被用到，都有更好的方案来替代

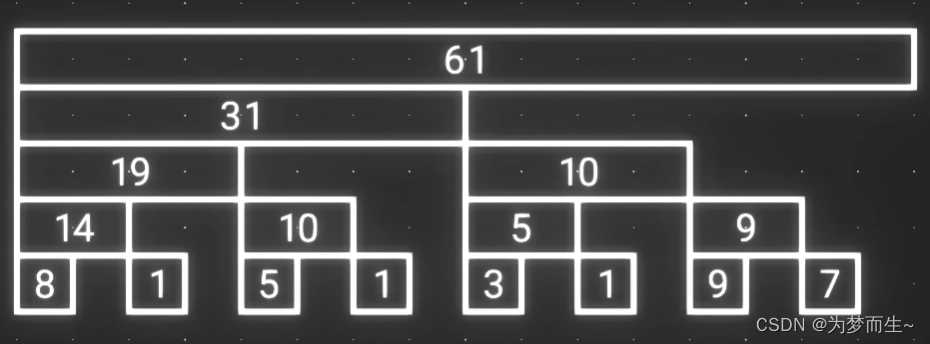
去除掉不会被用到的数字之后，剩下的数字正好是$n$个，这与数组的长度是一样的

所以，我们可以用一个与原数组长度相同的数组来装下这些数，这个数组就是一颗树状数组，数组中的每一个元素都对应下面的每一个区间，这些区间表示的都是每个对应的区间和

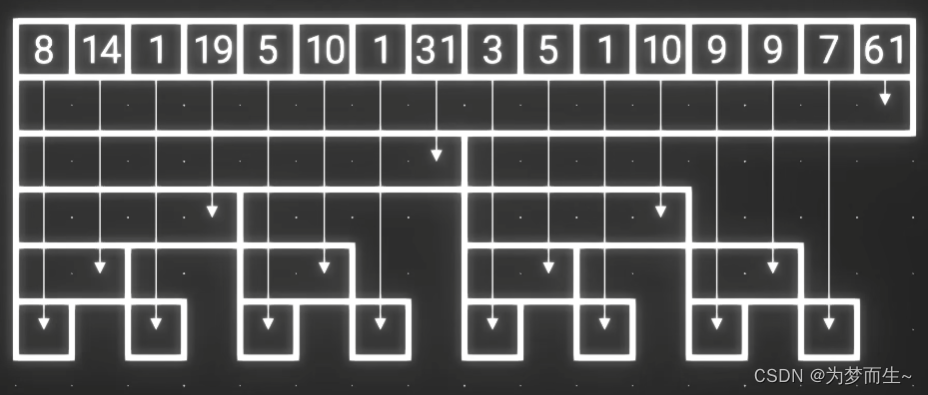
求和时，我们只需要找到对应的区间，将这些区间相加即可找到答案

修改某个数据时，我们也只需要向上找到包含它的所有区间修改即可

所有查询以及修改元素的操作，都可以在$O(\log n)$的时间复杂度内完成

3.2 树状数组的数学推导※

对于一个数$x$，我们可以把它分解成二进制的形式：
$2^{i_k}+2^{i_{k-1}}+2^{i_{k-2}}+...+2^{i_1}$，其中，$2^{i_k}$表示$x$的最高二进制位，$2^{i_1}$表示最低二进制位，$i_k\ge i_{k-1}\ge ...\ge i_1(k\le \log x)$

假设我们要求$1-x$的和，我们可以把区间分成$k$个区间

$(x-2^{i_1},x]$
$(x-2^{i_1}-2^{i_2},x-2^{i_1}]$
$...$
$(0,x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}}]$

这样我们把$x$分成了$\log x$个区间，如果我们把所有区间的和都预处理出来，最多只需要加$\log x$次就可以将区间和算出来

如何预处理这些数呢？

我们看一下这些区间有什么性质：

• 首先，每个区间都包含$2^i$个数
• 每个区间$(L,R]$的长度一定是$R$的二进制表示的最后一位$1$所对应的次幂

所以，利用lowbit函数，我们可以把贝格区间简化为$(R-lowbit(R)+1,R]$（该函数的定义如下）

def lowbit(x):return x & -x

于是，我们如果想用数组来记录区间和，可以用c[R]来表示区间和：c[x] = a[x - lowbit(x) + 1, x]

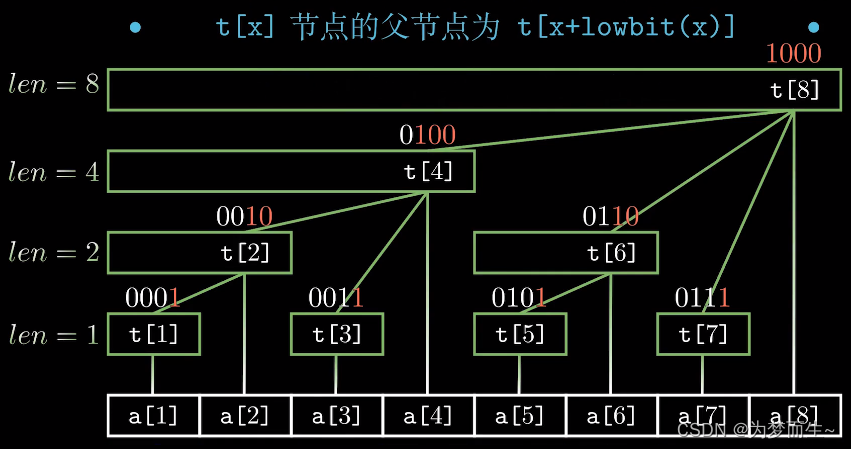
下面来看一下c[x]之间的关系：

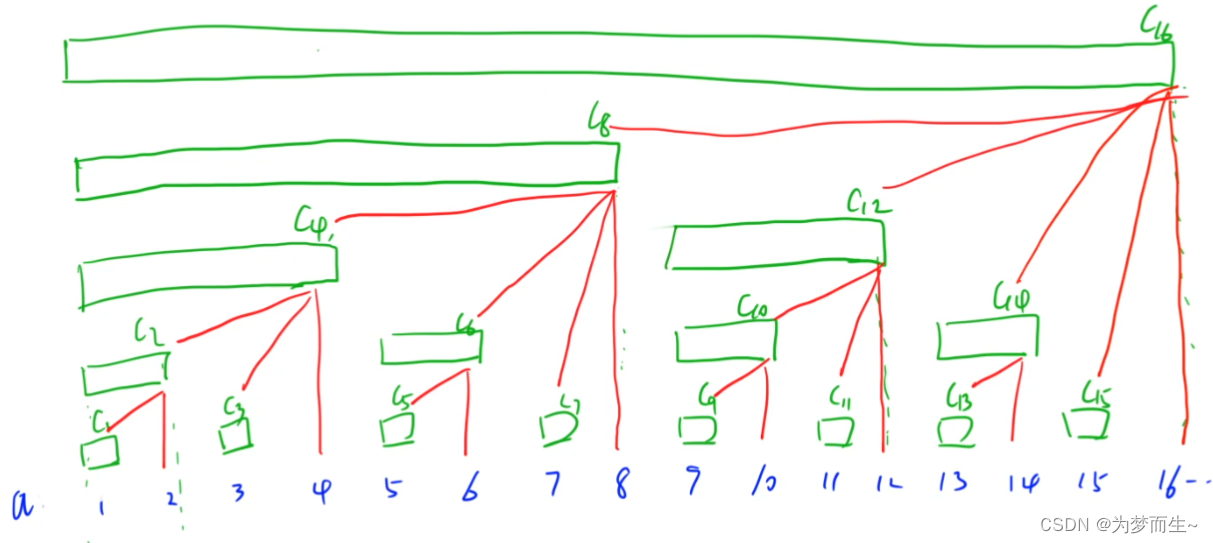
经过这样的数学推导之后，我们得到了与上面介绍中一致的形式

下面来介绍一下如何计算的数学推导

• 给出x，如何找到x的所有子节点

假设$x>0$，则必然存在最后一位$1$，假设这一位$1$后面有$k$个$0$，我们让$x-1$，则后面有连续的$k$个$1$，这每个$1$都对应一个儿子，我们找每个儿子只需要每次减去最后一位$1$，一直减$k$次，直到变成$0$

二进制表示解释如下：

c[x] ~ (x - lowbit(x) + 1, x]
x - 1 ~ ...1000(k个0)
儿子区间1 ： (...0111, ...0110]
儿子区间2 ： (...0110, ...0100]
儿子区间3 ： (...0100, ...0000]

• 如何通过子节点找父节点？

这个与找儿子结点是相反的，是一个迭代的过程，通常用于修改结点

假设给定一个x，修改完a[x]之后要修改哪些区间和？

假设$p$是一个父节点，它的二进制表示要满足要找子节点之前的形式（最后一位1后面跟着若干个0），那么它的子节点一定满足那个1变成0，后面跟若干个1，后面是若干个0

我们只需要把上面的过程逆过来就可以了

每次加上一个lowbit(x)，就找到直接父节点，然后一直往上加，直到加到那个父节点的位置是1，一共加$\log x$次，就可以找到所有父节点

对于一个要修改的a[x]，修改操作的代码是：

for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;

要想明白的是：为什么改完x之后，只需要更新tr数组的最多这么logx个位置（结合上面的黑白图）

查询（1~x的区间和）操作的代码（找子区间）：

for(int i = x; i; i -= lowbit(x)) res += tr[i];

---

部分内容及灵感来源：
https://www.bilibili.com/video/BV1ce411u7qP/
https://www.acwing.com/file_system/file/content/whole/index/content/172493/