目录
- 引言
- 概念
- 一、鱼塘钓鱼
- 二、技能升级
- 三、序列
引言
关于这个多路并归蓝桥杯考的不是很多,如果要出的话,可能模型都会差不多,因为不会出太难的题,难题基本上都是贪心、DP之类的,所以好好刷题刷熟练就行了,见过熟悉即可,加油!
概念
多路归并:首先可以参考博客算法刷题:归并排序、归并排序,这个多路归并其实就是一种类型的题目,还是要因题而异。
一、鱼塘钓鱼
标签:多路归并
思路: 1. 1. 1. 首先核心就是则个人钓鱼不会折返跑,因为每个鱼塘钓的鱼的数量是和你钓的次数有关,和时间无关,如果你又折返跑回来钓的话,还不如就直接在上一次的鱼塘多钓几次,还浪费路上的时间,所以最优解肯定是一条直线,而不会是来回的跑,因为这个 N N N 比较小,所以我们可以直接枚举最远的池塘数来计算最大值。 2. 2. 2. 我们可以提前把路程减去,然后只剩下钓鱼的时间了,所以就相当于在这多个鱼塘里钓,由于钓一次都是一分钟,并且没有路程的计算,所以就挑最大的几个就行了,也就是多个数 a [ i ] a[i] a[i] ,每个数取了就递减 d [ i ] d[i] d[i] 个,求最多能取多少个数,直接拿堆来模拟即可。
题目描述:
有 N 个鱼塘排成一排,每个鱼塘中有一定数量的鱼,例如:N=5 时,如下表:鱼塘编号 1 2 3 4 5
第1分钟能钓到的鱼的数量(1..1000) 10 14 20 16 9
每钓鱼1分钟钓鱼数的减少量(1..100) 2 4 6 5 3
当前鱼塘到下一个相邻鱼塘需要的时间(单位:分钟) 3 5 4 4
即:在第 1 个鱼塘中钓鱼第 1 分钟内可钓到 10 条鱼,第 2 分钟内只能钓到 8 条鱼,……,第 5 分钟以后再也钓不到鱼了。从第 1 个鱼塘到第 2 个鱼塘需要 3 分钟,从第 2 个鱼塘到第 3 个鱼塘需要 5 分钟,……给出一个截止时间 T,设计一个钓鱼方案,从第 1 个鱼塘出发,希望能钓到最多的鱼。假设能钓到鱼的数量仅和已钓鱼的次数有关,且每次钓鱼的时间都是整数分钟。输入格式
共 5 行,分别表示:
第 1 行为 N;
第 2 行为第 1 分钟各个鱼塘能钓到的鱼的数量,每个数据之间用一空格隔开;
第 3 行为每过 1 分钟各个鱼塘钓鱼数的减少量,每个数据之间用一空格隔开;
第 4 行为当前鱼塘到下一个相邻鱼塘需要的时间;
第 5 行为截止时间 T。输出格式
一个整数(不超过231−1),表示你的方案能钓到的最多的鱼。数据范围
1≤N≤100 ,1≤T≤1000
输入样例:
5
10 14 20 16 9
2 4 6 5 3
3 5 4 4
14
输出样例:
76
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;const int N = 110;int n, T;
int a[N], d[N], l[N];LL work(int x, int t)
{if(t <= 0) return 0;priority_queue<PII> heap;for(int i = 1; i <= x; ++i) heap.push({a[i], i});LL res = 0;while(t-- && heap.size()){auto t1 = heap.top(); heap.pop();int v = t1.first, p = t1.second;res += v;if(v - d[p] > 0) heap.push({v-d[p], p});}return res;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; ++i) cin >> a[i];for(int i = 1; i <= n; ++i) cin >> d[i];for(int i = 2; i <= n; ++i) {cin >> l[i];l[i] += l[i-1];}cin >> T;LL res = 0;for(int i = 1; i <= n; ++i){res = max(res, work(i, T - l[i]));}cout << res << endl;
}
二、技能升级
标签:多路归并
思路:明显可以看出这道题是上一道题的简化版,也就是这道题是包含在上道题里的,也就是 w o r k work work 函数,但由于这道题的 M M M 的值比较大,所以如果用 h e a p heap heap 来做的话,能过 7 12 \frac{7}{12} 127 个数据,所以要另辟蹊径了。我们假设所有的可能的数第 M M M 个数值为 mid ,那么最大值就是取前 M M M 个数了,所以我们只要 mid 确定了下来,剩余就可以遍历每个序列用数学公式就能计算出来总和。然后我们能够知道小于等于 mid 的个数一定是大于等于 M 的,所以具有二段性可以用二分来写,具体细节见代码。
题目描述:
小蓝最近正在玩一款 RPG 游戏。他的角色一共有 N 个可以加攻击力的技能。其中第 i 个技能首次升级可以提升 Ai 点攻击力,以后每次升级增加的点数都会减少 Bi。⌈AiBi⌉(上取整)次之后,再升级该技能将不会改变攻击力。现在小蓝可以总计升级 M 次技能,他可以任意选择升级的技能和次数。请你计算小蓝最多可以提高多少点攻击力?输入格式
输入第一行包含两个整数 N 和 M。
以下 N 行每行包含两个整数 Ai 和 Bi。输出格式
输出一行包含一个整数表示答案。数据范围
对于 40% 的评测用例,1≤N,M≤1000;
对于 60% 的评测用例,1≤N≤104,1≤M≤107;
对于所有评测用例,1≤N≤105,1≤M≤2×109,1≤Ai,Bi≤106。输入样例:
3 6
10 5
9 2
8 1
输出样例:
47
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e5+10;int n, m;
int a[N], b[N];bool check(int mid)
{LL sum = 0;for(int i = 1; i <= n; ++i){if(a[i] >= mid){sum += (a[i] - mid) / b[i] + 1;}}return sum >= m;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1; i <= n; ++i) cin >> a[i] >> b[i];int l = 0, r = 1e6;while(l < r){int mid = (LL)l + r + 1 >> 1;if(check(mid)) l = mid;else r = mid - 1;}LL res = 0, cnt = 0;for(int i = 1; i <= n; ++i){if(a[i] >= r){int c = (a[i] - r) / b[i] + 1;int end = a[i] - (c - 1) * b[i];cnt += c;res += (LL)(a[i] + end) * c / 2;}}cout << res - (cnt - m) * r << endl; // 可能会有多个r,数量超过了mreturn 0;
}
三、序列
标签:多路归并
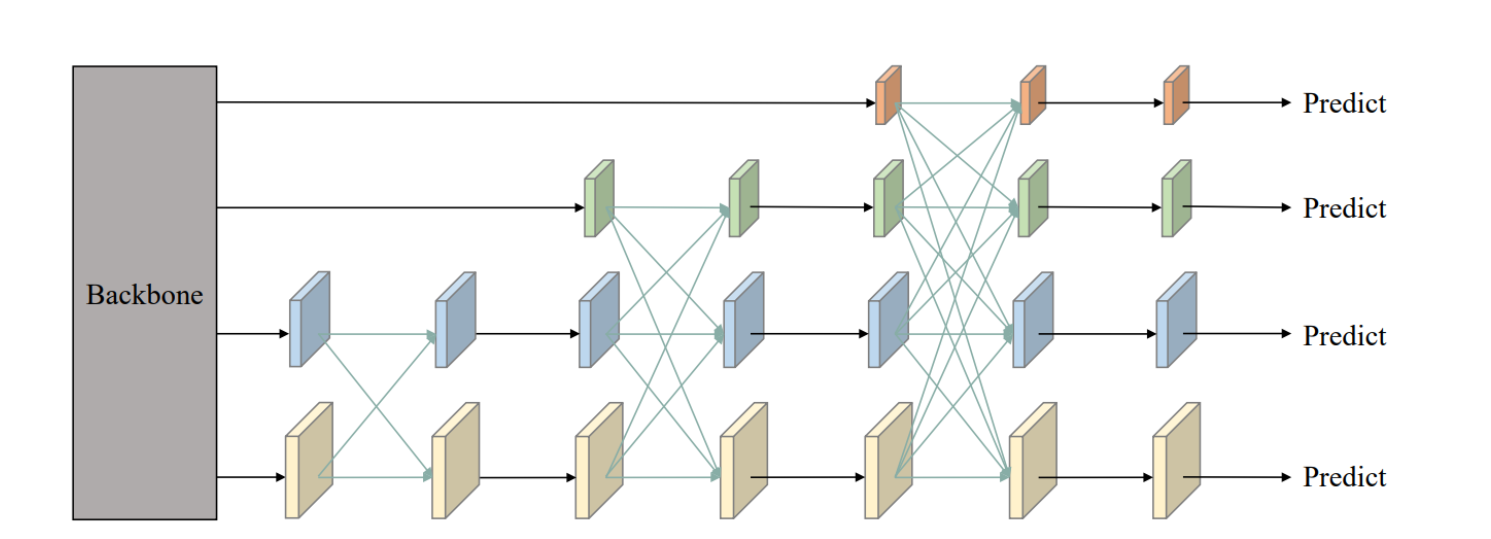
思路:这是一个典型的从 m m m 行 n n n 列中,每一行选一个数组,求选到的数字之和最小的 n n n 个。我们可以先两行两行的合并找到最小的 n n n 个,然后遍历 m − 1 m - 1 m−1 次,这样最后的 n n n 个数字就是最小的了。然后两个合并,我们可以先把 a a a 数组排个序,然后把这 n 2 n ^ 2 n2 的数排成 n n n 组,如下图所示,由于 a a a 是排好序了,所以每组最小的就是最前边的那个,然后把这 n n n 个数加入到堆中,然后记下当前下标,然后再变成每组下一个数即可,这样下来的 n n n 个数就是最小的了。

题目描述:
给定 m 个序列,每个包含 n 个非负整数。现在我们可以从每个序列中选择一个数字以形成具有 m 个整数的序列。很明显,我们一共可以得到 nm 个这种序列,然后我们可以计算每个序列中的数字之和,并得到 nm 个值。现在请你求出这些序列和之中最小的 n 个值。输入格式
第一行输入一个整数 T,代表输入中包含测试用例的数量。接下来输入 T 组测试用例。对于每组测试用例,第一行输入两个整数 m 和 n。接下在 m 行输入 m 个整数序列,数列中的整数均不超过 10000。输出格式
对于每组测试用例,均以递增顺序输出最小的 n 个序列和,数值之间用空格隔开。每组输出占一行。数据范围
0<m≤1000,0<n≤2000
输入样例:
1
2 3
1 2 3
2 2 3
输出样例:
3 3 4
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;const int N = 2010;int T;
int m, n;
int a[N], b[N], c[N];void merge()
{priority_queue<PII, vector<PII>, greater<PII>> heap;for(int i = 0; i < n; ++i) heap.push({a[0] + b[i], 0});for(int i = 0; i < n; ++i){auto t = heap.top(); heap.pop();int v = t.first, p = t.second;c[i] = v;heap.push({v - a[p] + a[p+1], p+1});}memcpy(a, c, sizeof a);
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> T;while(T--){cin >> m >> n;for(int i = 0; i < n; ++i) cin >> a[i];sort(a, a+n);for(int i = 0; i < m - 1; ++i){for(int j = 0; j < n; ++j) cin >> b[j];merge();}for(int i = 0; i < n; ++i) cout << a[i] << " ";cout << endl;}return 0;
}


![【动态规划.3】[IOI1994]数字三角形 Number Triangles](https://img-blog.csdnimg.cn/direct/7931675d8d7f4db5a0d78e51aae6ff94.png)

![[Buuctf] [MRCTF2020]Transform](https://img-blog.csdnimg.cn/direct/82715af271054cf19779368166013c2e.png)