目录
1,题目
2,代码
2.1递归思想
2.2队列--迭代思想
3,学习与总结
1,题目
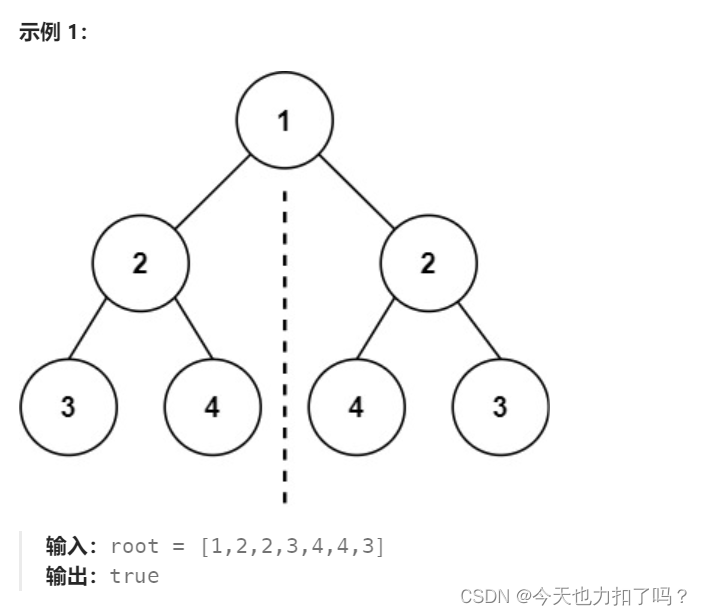
给你一个二叉树的根节点 root , 检查它是否轴对称。
2,代码
2.1递归思想
return dfs(left.left, right.right) && dfs(left.right, right.left);这行代码的含义是,只有当这两个递归调用都返回true时,整个表达式才会返回true这里的
&&是逻辑与运算符,用于确保以下两个主要条件同时满足:
dfs(left.left, right.right)检查当前节点的左子节点的左子树与右子节点的右子树是否对称。如果它们不对称(即,函数返回false),则整个表达式立即返回false,不再继续计算后面的条件。dfs(left.right, right.left)检查当前节点的左子节点的右子树与右子节点的左子树是否对称。这个调用只有在第一个调用返回true的情况下才会被评估,因为&&运算符具有短路特性,即如果第一个操作数为false,则不会评估第二个操作数。加上
&&确保了只有在两对子树同时满足对称条件时,函数才会返回true,这对于验证树的对称性是必要的。如果任何一对子树不对称,整个树就不对称,函数就会返回false。
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {boolean}*/
var isSymmetric = function(root) {function dfs(left,right){if(left === null &&right === null){return true;}if(left===null || right === null){return false;}if(left.val != right.val ){return false;}return dfs(left.left,right.right) && dfs(left.right,right.left);}if(root === null){return true;}return dfs(root.left,root.right);
};2.2队列--迭代思想
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {boolean}*/
var isSymmetric = function(root) {// 借助队列if(root === null || root.left===null && root.right===null){return true;}// 数组模拟队列let queues=[];queues.push(root.left);queues.push(root.right);while(queues.length > 0){const left = queues.shift();const right = queues.shift();if(left === null && right===null){continue;}if(left === null || right===null){return false;}if(left.val != right.val){return false;}//将左节点的左孩子, 右节点的右孩子放入队列queues.push(left.left);queues.push(right.right);//将左节点的右孩子,右节点的左孩子放入队列queues.push(left.right);queues.push(right.left); }return true;
};3,学习与总结
树的递归思想 对我来说 在上难度了,多次思考,多问为什么,帮助自己提升自己的思维!
勉励自己:贵在坚持!