一、题目
1、题目描述
给你一个整数数组
nums和一个 正 整数k。你可以选择数组的任一 子序列 并且对其全部元素求和。数组的 第 k 大和 定义为:可以获得的第
k个 最大 子序列和(子序列和允许出现重复)返回数组的 第 k 大和 。
子序列是一个可以由其他数组删除某些或不删除元素排生而来的数组,且派生过程不改变剩余元素的顺序。
注意:空子序列的和视作
0
2、接口描述
class Solution {
public:long long kSum(vector<int>& nums, int k) {}
};3、原题链接
2386. 找出数组的第 K 大和 - 力扣(LeetCode)
二、解题报告
1、思路分析
首先明确最大子序列和就是所有正数之和sum
那么第2大就是sum加上一个非负数或者从正数中拿掉一个
那么我们可以将原数组全部取绝对值,然后求取绝对值后的第k - 1小序列和s
那么答案就是sum - s
F1 二分+枚举子集
给定mid,如何判断是否至少有k个子序列和不大于mid
对于每个nums[i]都有选或不选两种情况,那么我们递归枚举子序列
正常而言,枚举所有子序列是2^n,但是我们没必要全部枚举
我们可以将nums按升序排序
如果枚举到i,上一个子序列和为s,那么如果s + nums[i] > mid,我们就剪枝
否则cnt++,然后继续向下枚举
我们发现递归次数和cnt+1的次数有关,而cnt最多加k次,所以我们可以O(k)解决
然后定义二分边界l = 0, r = sum(nums)(nums取绝对值且排序后)
不断二分即可
F2 转化为树上第k短路
我们考虑取绝对值且排序后nums枚举子集在树上表示如下:
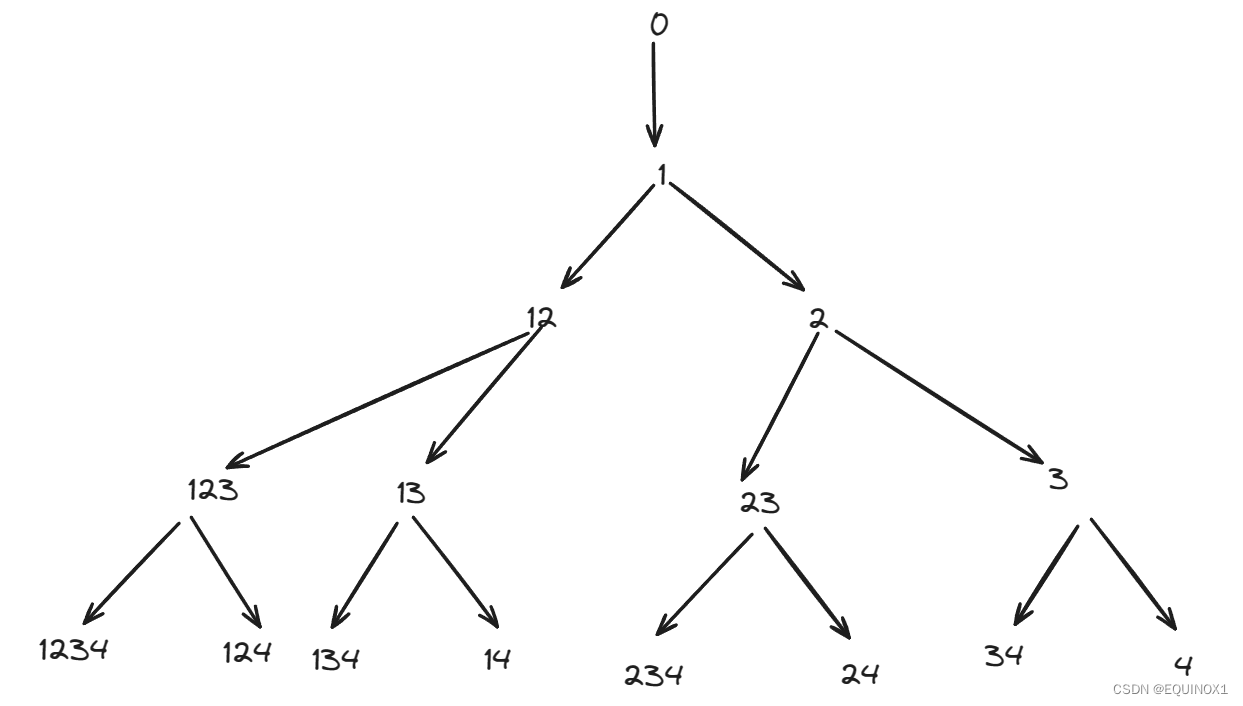
每个节点代表一个子序列,显然越往下节点的权值越大
那么我们只要找到从根节点出发的第k - 1短路即可
其实就是树上dijkstra,用小根堆存储节点权值和下一个元素的下标即可
2、复杂度
F1:时间复杂度:O(nlogn+klogU),即排序和二分 空间复杂度:O(min(k,n)),即取决于递归深度
F2:时间复杂度:O(nlogn+klogk)空间复杂度:O(k)
3、代码详解
F1
class Solution {
public:long long kSum(vector<int>& nums, int k) {long long sum = 0;for(int& x : nums) if(x >= 0) sum += x; else x = -x;sort(nums.begin(), nums.end());function<bool(long long)> check = [&](long long lim){int cnt = 1;function<void(int, long long)> dfs = [&](int i, long long s){if(cnt == k || i == nums.size() || s + nums[i] > lim) return;++cnt, dfs(i + 1, s + nums[i]), dfs(i + 1, s);};dfs(0, 0);return cnt == k;};long long l = 0, r = accumulate(nums.begin(), nums.end(), 0LL);while(l < r){long long mid = l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}return sum - r;}
};F2
class Solution {
public:long long kSum(vector<int>& nums, int k) {long long sum = 0;for(int& x : nums) if(x >= 0) sum += x; else x = -x;sort(nums.begin(), nums.end());priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;pq.emplace(0, 0);while(--k){auto [s, i] = pq.top();pq.pop();if(i < nums.size()) {pq.emplace(s + nums[i], i + 1);if(i) pq.emplace(s + nums[i] - nums[i - 1], i + 1);}}return sum - pq.top().first;}
};