1 排列组合的堆生成法
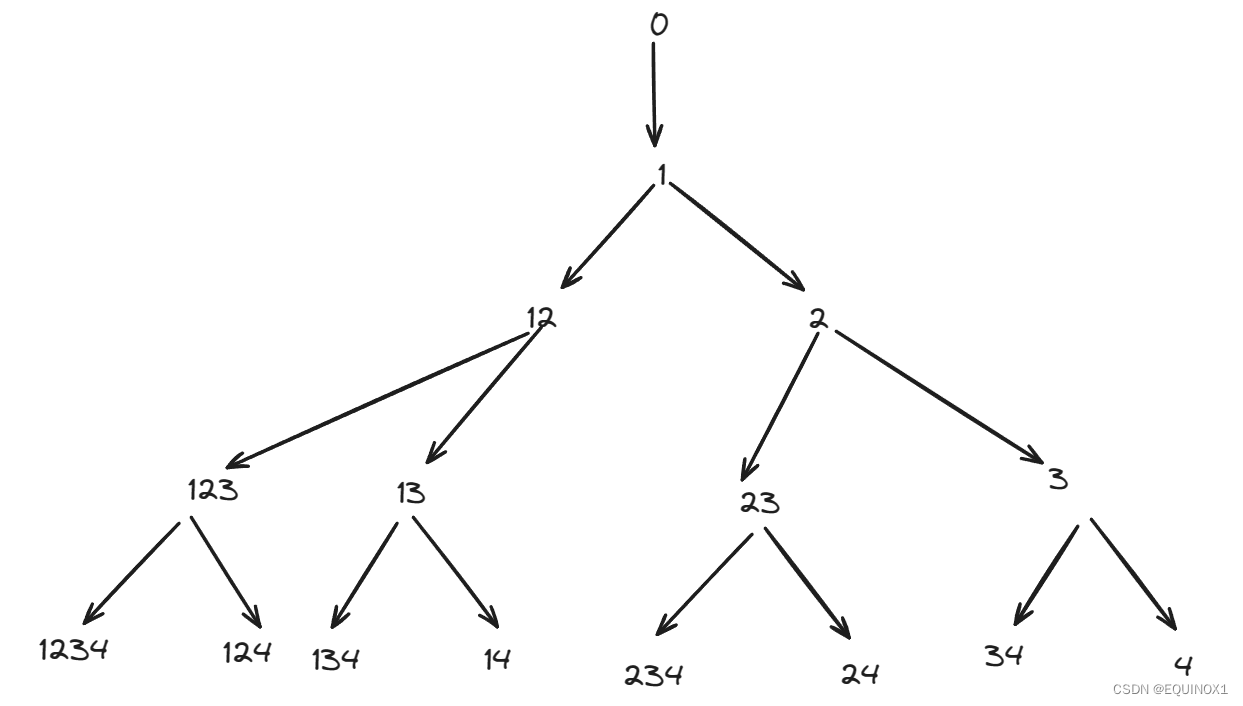
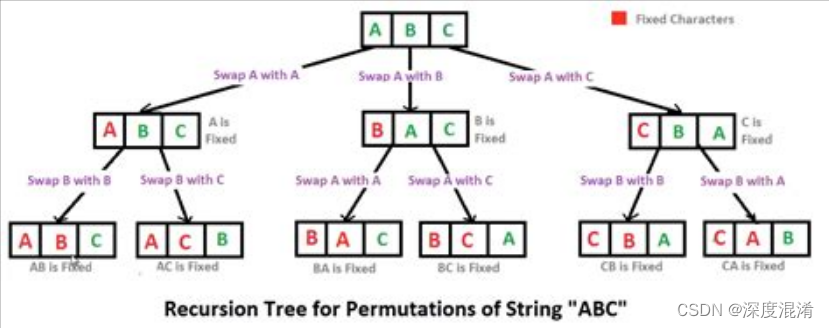
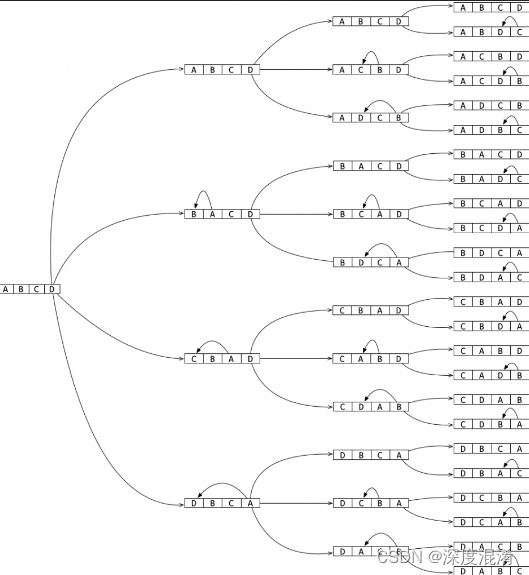
堆生成算法用于生成n个对象的所有组合。其思想是通过选择一对要交换的元素,在不干扰其他n-2元素的情况下,从先前的组合生成每个组合。
下面是生成n个给定数的所有组合的示例。
示例:
输入:1 2 3
输出:1 2 3
2 1 3
3 1 2
1 3 2
2 3 1
3 2 1
2 算法
算法生成(n-1)!前n-1个元素的排列,与其中每个元素相邻的最后一个元素。这将生成以最后一个元素结尾的所有置换。
如果n为奇数,则交换第一个和最后一个元素,如果n为偶数,则交换第i个元素(i是从0开始的计数器)和最后一个元素,并重复上述算法,直到i小于n。
在每次迭代中,算法将生成以当前最后一个元素结尾的所有组合。
3 源程序
using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Algorithm_Gallery
{
public static void Heap_Permutation(ref int[] a, int size, int n)
{
if (size == 1)
{
return;
}
for (int i = 0; i < size; i++)
{
Heap_Permutation(ref a, size - 1, n);
if (size % 2 == 1)
{
int temp = a[0];
a[0] = a[size - 1];
a[size - 1] = temp;
}
else
{
int temp = a[i];
a[i] = a[size - 1];
a[size - 1] = temp;
}
}
}
}
}

相关文章摘要:
摘要来源![]() https://cdmd.cnki.com.cn/Article/CDMD-10269-1012434174.htm
https://cdmd.cnki.com.cn/Article/CDMD-10269-1012434174.htm
堆是最基本的数据结构之一,对堆进行枚举,可以作为堆各类算法复杂性分析的有力工具,有着重要的意义。
堆的枚举一方面是计数,另一方面是生成。计数即推导公式计算出具有某种特征的堆的总数目;生成即一个一个地产生所有的具有某类特点的堆。堆是一种重要的二叉树,在数据排序、优先级队列、最短路径和最小生成树的求解以及一些网络优化问题上都有广泛的应用。
本文先对已有的枚举算法进行研究,分析不同算法的时间复杂度和空间复杂度,这包括二叉树的枚举和最大值堆的枚举以及左倾堆的枚举,在已有的堆枚举生成算法基础上,本文主要完成了以下工作: 首先结合对堆中各子树结点数以及堆结构的研究,以提高堆枚举生成算法的空间复杂度为目的,本文提出了“基于排列”的最大值堆的枚举生成算法。即在给定数中,通过排列组合算法,生成所有的排列,对排列进行判断,选出能够成为最大值堆中序序列的排列,运用此排列构造对应的最大值堆。考虑到最大值堆结构的递归性质,本文继续将判断的过程递归化,即以排列中的最大值为分界点(最大值作为堆的根结点),递归判断左排列(排列中最大值左边的序列)和右排列(排列中最大值右边的序列),是否能够分别构成堆左子树和右子树的中序序列。递归化的判断过程则是将已有排列划分成更多、更小的排列来判断。较之以往的最大值堆生成算法,基于排列的生成算法避免了以往两个互动栈所需O(n)的存储空间。 其次,本文在已有的“单个数判断法”和“层次判断法”的基础上,提出了“至下而上”的最大值堆的枚举生成算法。即该算法通过“单个数判断法”,先生成堆中最深层次中的结点;当已经生成堆中完整的一层时,通过“层次判断法”来判断是否满足堆中的一层,如果满足,则继续生成堆中往上一个层次的结点,不满足则重新生成该层,即由深层次向低层次构造一个堆。在以往的生成堆的过程中,主要考虑的是整个堆的生成,它从根结点开始,一层层往下生成一个完整的堆,只有在生成整个堆的时候,才可以知道堆的最后一层的元素及叶子结点的值。而“至下而上”的堆的生成改进了上述的不足,在生成堆的过程中,提前知道底层结点的值。为今后堆研究过程中,对底层结点的运用提供了一个可靠的方法。相比较“基于排列”的枚举算法,本算法在空间复杂度上,增加了O(n)的存储空间。但是“至下而上”的最大值堆的枚举生成算法,采用“单个数判断法”和“层次判断法”两个基本方法减少了冗余步骤的生成。实验表明,本算法的生成时间开销相比较“基于排列”的枚举算法平均减少了80%。 本文的最后,对所有堆的枚举算法进行了总结,并且提出了对堆枚举生成算法的改进方法和展望。以上这些工作为进一步研究堆的性质提供了有力的帮助,也为今后进一步的研究奠定了基础。
4 源代码
using System;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public static partial class Algorithm_Gallery{public static void Heap_Permutation(ref int[] a, int size, int n){if (size == 1){return;}for (int i = 0; i < size; i++){Heap_Permutation(ref a, size - 1, n);if (size % 2 == 1){int temp = a[0];a[0] = a[size - 1];a[size - 1] = temp;}else{int temp = a[i];a[i] = a[size - 1];a[size - 1] = temp;}}}}
}