在数字化浪潮的推动下,微信小程序作为一种轻便、高效的移动应用形式,正成为越来越多企业开展电商业务的重要平台。而分销商城微信小程序的出现,更是为企业带来了前所未有的机遇。通过分销商城微信小程序,企业不仅能够拓宽销售渠道,提升品牌影响力,更能够显著增强用户粘性,促进复购率的提升。
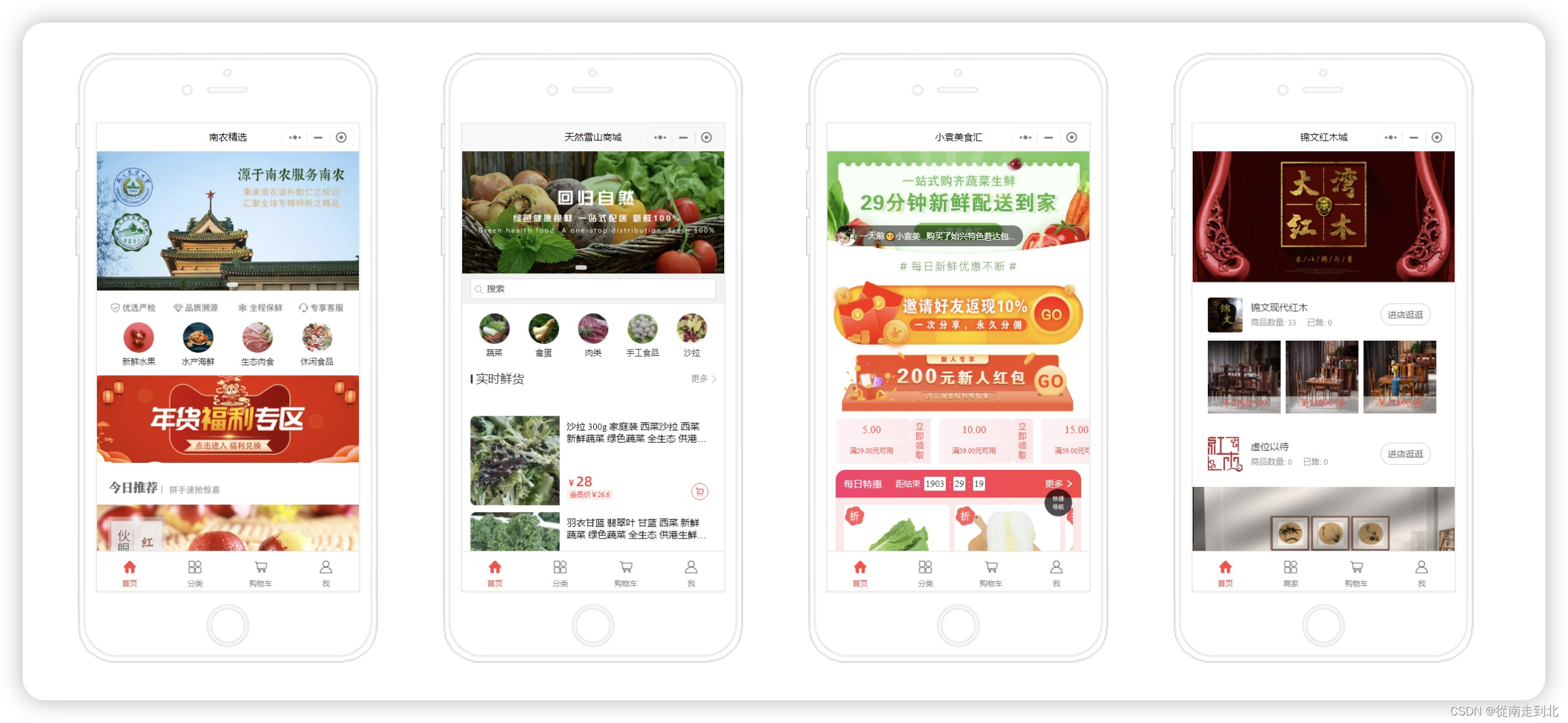
首先,分销商城微信小程序能够增强用户粘性。微信小程序具有无需下载安装、即用即走的特点,使得用户可以轻松访问和使用。而分销商城微信小程序则通过丰富的商品展示、便捷的购物流程以及个性化的推荐算法,为用户提供了更加优质的购物体验。用户可以在小程序内轻松浏览商品、了解详情、下单购买,并享受快速的物流配送服务。这种便捷、高效的购物体验,使得用户更愿意在微信小程序内进行购物,从而增强了用户粘性。
其次,分销商城微信小程序能够促进复购率的提升。通过微信小程序,企业可以建立起与用户的直接联系,实现精准营销和个性化服务。通过收集用户的购物数据、行为偏好等信息,企业可以深入分析用户的购物需求,为用户推送个性化的商品推荐和优惠活动。这种个性化的服务能够提升用户的满意度和忠诚度,使得用户更愿意在微信小程序内进行复购。此外,企业还可以通过微信小程序的社交属性,开展拼团、分享等活动,鼓励用户邀请亲朋好友一起购物,从而进一步提升复购率。
除了以上两点,分销商城微信小程序还具有其他诸多优势。例如,通过微信小程序,企业可以实现线上线下融合,为用户提供更加全面的服务;同时,微信小程序的低成本、易推广等特点,也使得企业能够以更低的成本获得更多的流量和用户。这些优势共同作用下,使得分销商城微信小程序成为企业开展电商业务的得力助手。
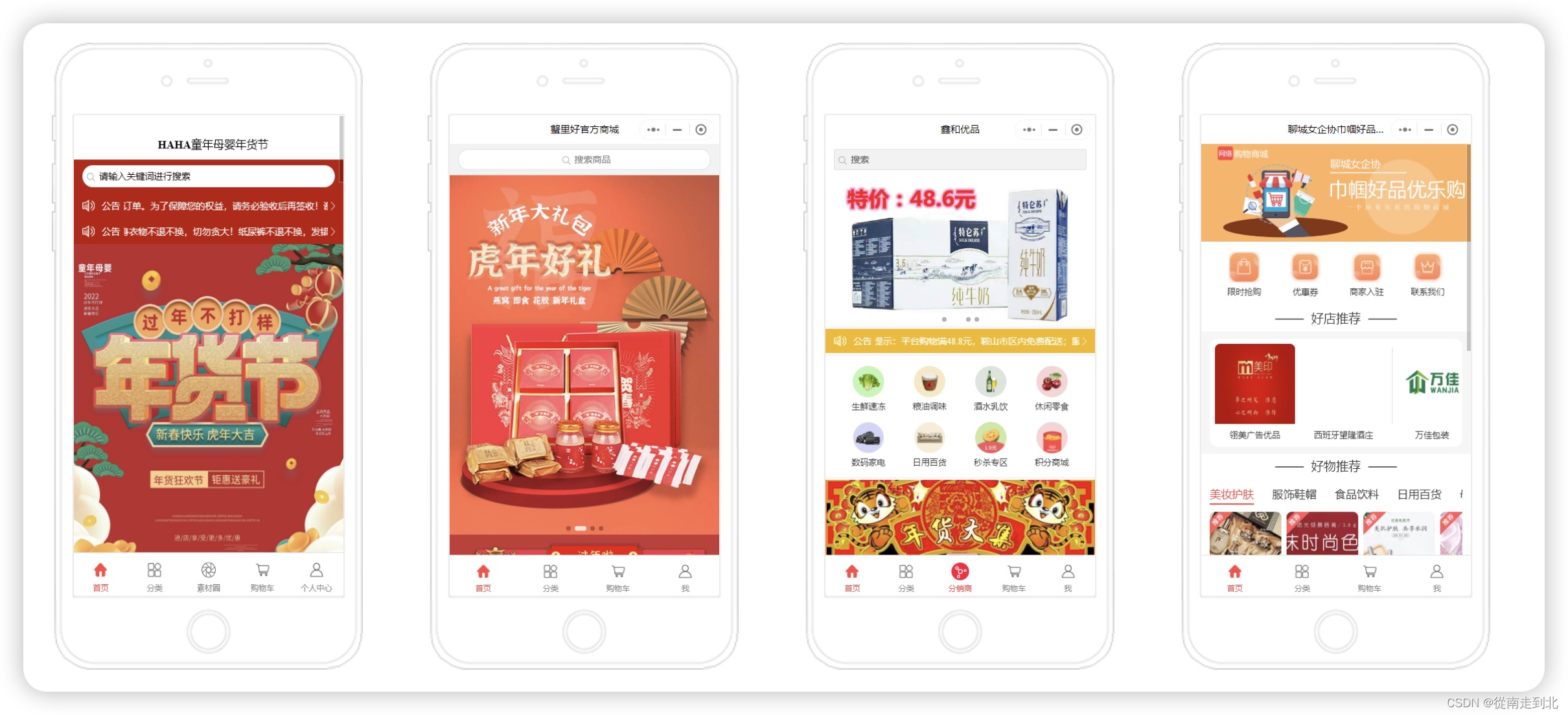
综上所述,分销商城微信小程序通过增强用户粘性、促进复购率提升等方式,为企业带来了显著的商业价值。在未来的发展中,随着技术的不断进步和市场的不断变化,分销商城微信小程序将继续发挥重要作用,助力企业实现数字化转型和电商业务的快速发展。因此,对于有意开展电商业务的企业来说,积极拥抱微信小程序、打造优质的分销商城微信小程序,将成为其提升竞争力、实现可持续发展的关键一环。