leetcode 904. 水果成篮 | 中等难度

1. 题目详情

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果 种类 。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。
给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。

示例 1：
输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。

示例 2：
输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。

示例 3：
输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。
示例 4：

输入：fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：可以采摘 [1,2,1,1,2] 这五棵树。

提示：
$1<=fruits.length<=10^5$
$0<=fruits[i]<fruits.length$

1. 原题链接

leetcode 904. 水果成篮

2. 基础框架

● Cpp代码框架

class Solution {
public:int totalFruit(vector<int>& fruits) {}
};

2. 解题思路

1. 题目分析

$(1)$ 本题是一道阅读理解题，首先理清题意：一个数组fruits，数组内的元素表示每棵树上水果的种类。我们从可以从任意一棵树开始采摘，但是每棵树只能采摘一次且只能向后移动，采摘的水果数量没有限制，但是只能采摘最多2种类型的水果。
类似于固定一个初始位置left，然后从左到右依次遍历数组fruits。题目又多了水果类型不超过2种的条件，所以在遍历数组fruits时需要额外记录水果类型和出现次数的对应关系，即key,val键值对。
$(2)$ 题目本质是求连续子数组的最大长度，只不过本题多了一个条件。
$(3)$ 先来看看暴力枚举思路：
以left位置为起始位置，right从左到右依次遍历数组fruits，使用哈希表记录已遍历到子数组内水果类型及其出现的次数，len记录连续子数组的最大长度。
如果right位置的新水果加入后，水果类型 > 2，那么说明right及其之后的所有水果都不会满足连续子数组且水果类型不超过2了，right及其之后的位置也没有必要继续判断了，可以直接进行left在下一个位置的判断了；
如果right位置的新水果加入后，水果类型 <= 2，[left, right]位置的水果是满足条件的，所以更新len = max(len, right - left + 1)；
对于每一次以新的left作为起始位置，right都要回退到left位置重新开始遍历，哈希表也需要清空，重新等待元素进入；
$(4)$

2. 算法原理

$(1)$ 暴力枚举有什么可以优化的地方呢？
假设以某一个left为起始位置，right从left开始向右依次遍历数组fruits，每次遍历的水果都进入哈希表hash。
恰好本次right位置的新水果fruits[right]进入哈希表后，哈希表的元素[key,val]大于2，让我们定格在此：
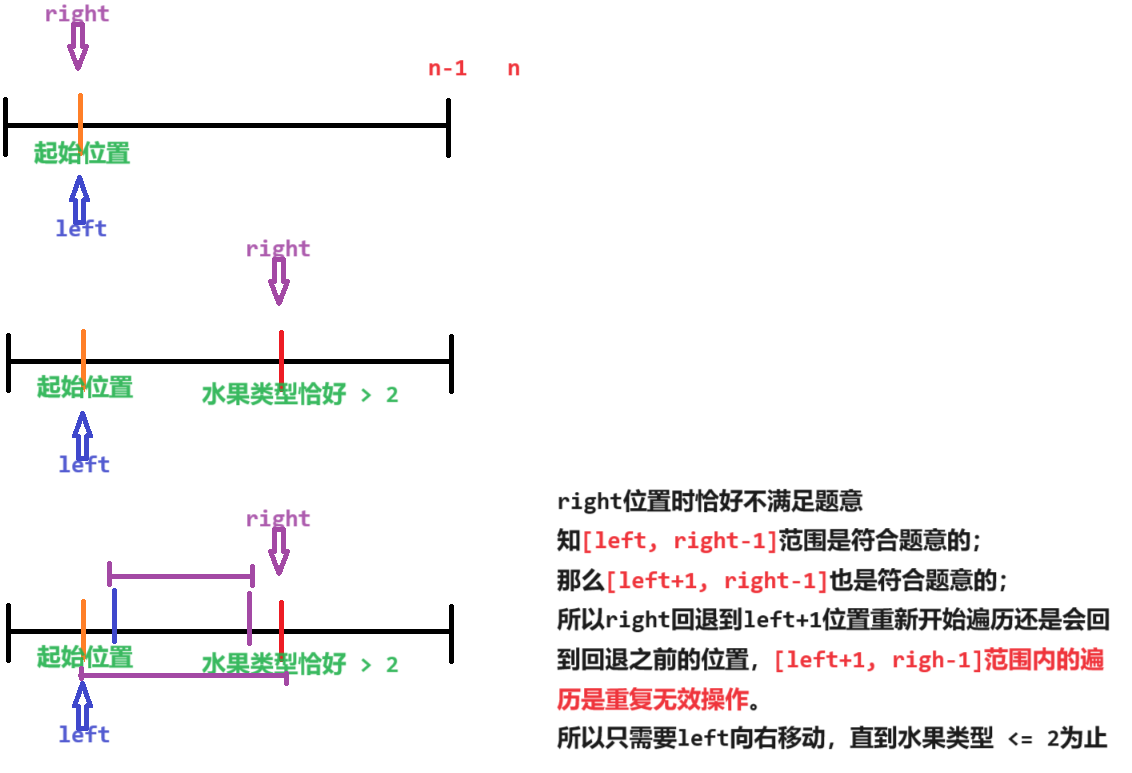
暴力枚举的思路是：既然以left为起始的子数组已经不满足题意了，那么我left就右移，以新位置开始，哈希表hash清空，right回退并以新的left位置重新遍历数组frutis。

在本次假设下，right位置元素是恰好不满足题意的，那么可知[left, right-1]区间的所有元素是一定满足题意的。
那么有必要让right回退到新left吗？哈希表hash有必要全部清空吗？

首先知道[left+1,right-1]区间一定是满足题意的，那么如果right回退到left+1位置，而[left+1,right-1]区间一定满足题意，那么该区间就会被重新遍历并以此加入哈希表hash，然后right又会来到回退之前的位置，在此位置可能有三种情况：right位置元素加入后
总水果类型小于等于2，那么right继续++向右遍历即可；
总水果类型还是大于2，那么left需要继续右移。
无论哪一种情况，right都不需要回退，只可能是不动或向右移动。

$(2)$ 滑动窗口
$(3)$ 初始化：left = 0, right = 0，哈希表hash，长度记录len；
$(4)$ 进窗口：right位置元素进入哈希表
$(5)$ 判断：在哈希表中水果类型 > 2时
$(6)$ 出窗口：哈希表hash中对应水果类型fruits[left]的计数–，特别的如果计数减到了0，说明没有此种类型水果了，需要在哈希表hasn中删除该类型，且left右移1位；
$(7)$ 更新结果： 到这一步说明[left, righ]范围内元素都是满足题意的，可以更新结果len = max(len, right-left)；

3. 时间复杂度

$O(n^{)}$

3. 代码实现

class Solution {
public:int totalFruit(vector<int>& fruits) {//unordered_map<int, int> hash;int hash[100001] = { 0 };int ret = 0;int l = 0, r = 0;int n = fruits.size();int kinds = 0;while(r < n){if(hash[fruits[r]] == 0) kinds++;hash[fruits[r]]++;//进窗口//while(hash.size() > 2){//判断while(kinds > 2){  hash[fruits[l]]--;//出窗口//if(hash[fruits[l]] == 0) hash.erase(fruits[l]);if(hash[fruits[l]] == 0) kinds--;l++;}ret = max(ret, r - l + 1);//更新结果r++;}return ret;}
};

4. 知识与收获

$(1)$ 本题需要先理清题意，找出本质：连续子数组的最大长度。

---

$The$ $End$