图【数据结构】

文章目录

  • 图的基本概念
  • 邻接矩阵
  • 邻接表
  • 图的遍历
    • BFS
    • DFS

图的基本概念

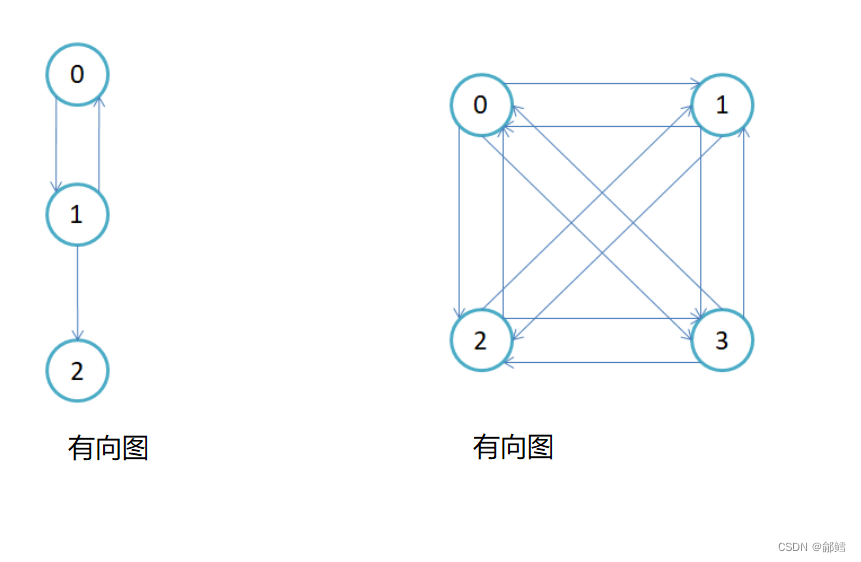
图是由顶点集合及顶点间的关系组成的一种数据结构
顶点和边：图中结点称为顶点

权值:边附带的数据信息

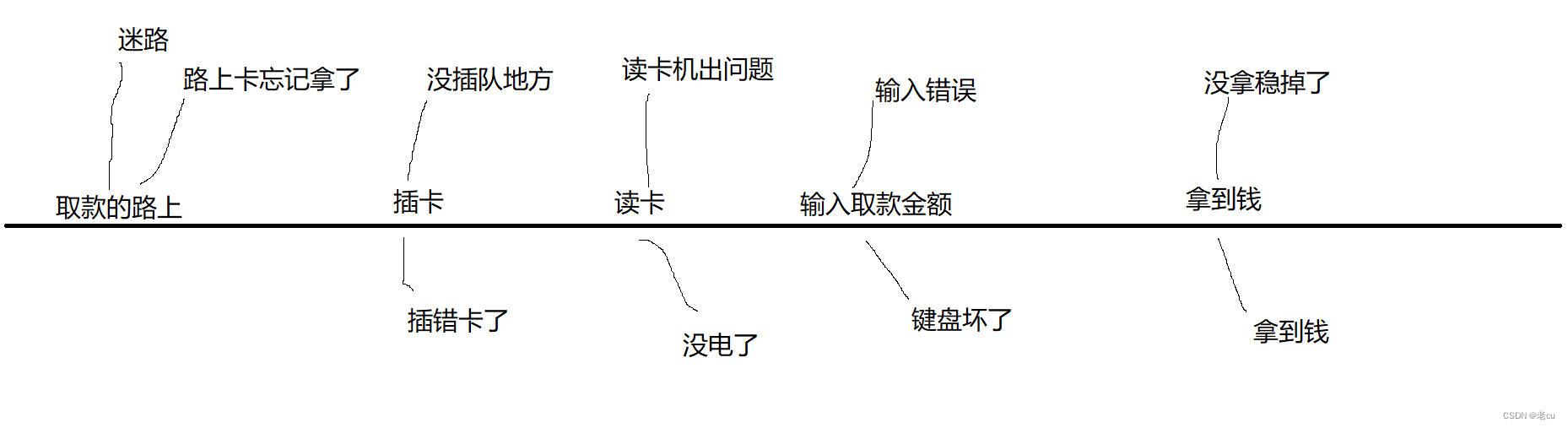
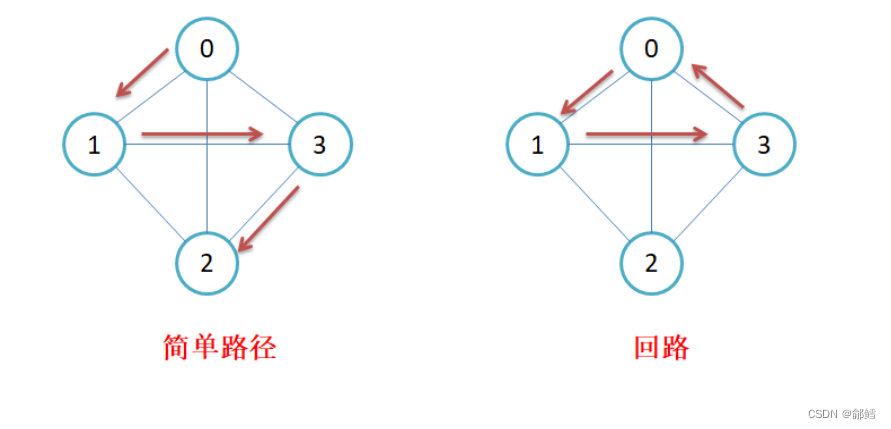
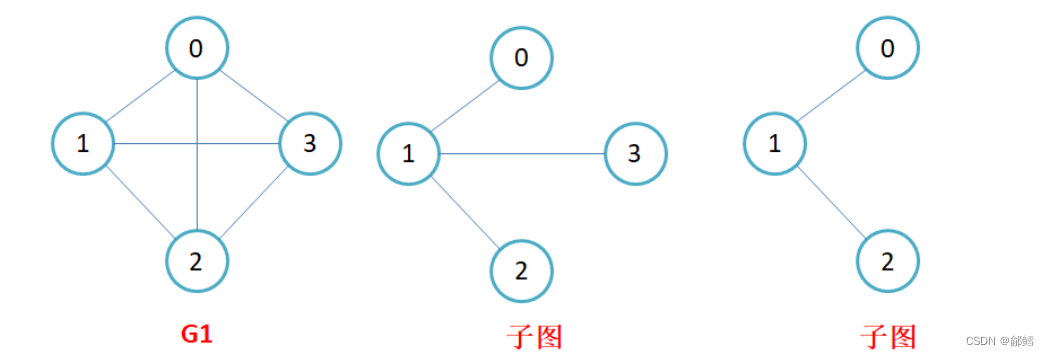
在这里插入图片描述

在这里插入图片描述
路径 ： 在这里插入图片描述

简单路径 和 回路：在这里插入图片描述

子图：设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图
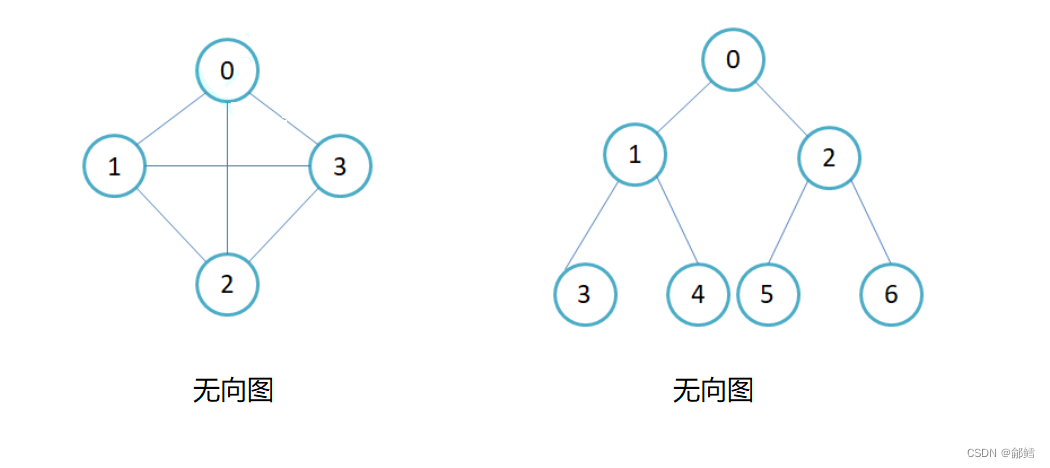
在这里插入图片描述

连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图

生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边

生成树就是用最少的边连通起来

最小生成树:构成生成树这些边加起来权值是最小的。

顶点的度：
**加粗样式**
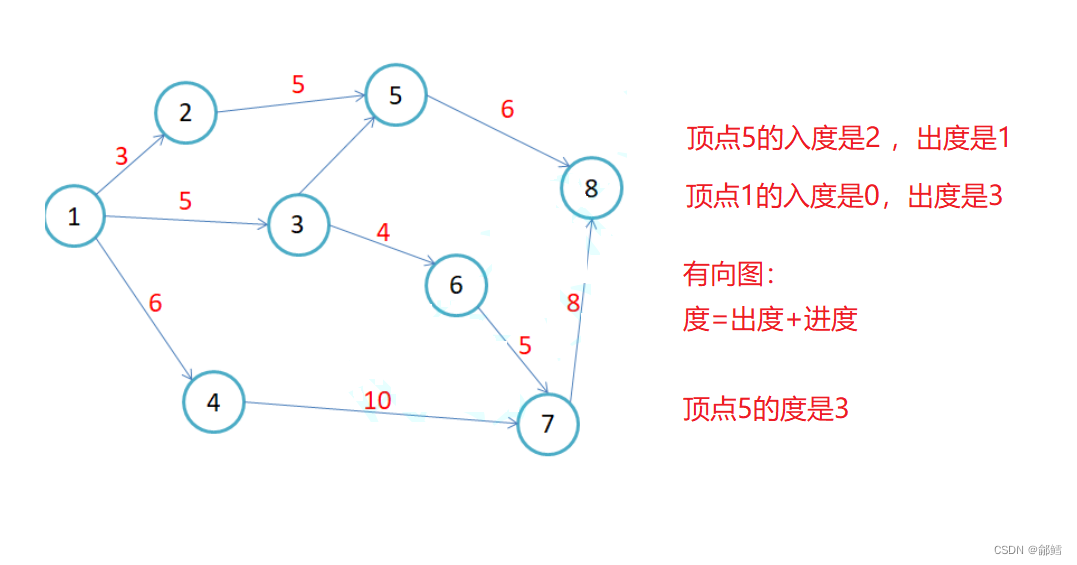
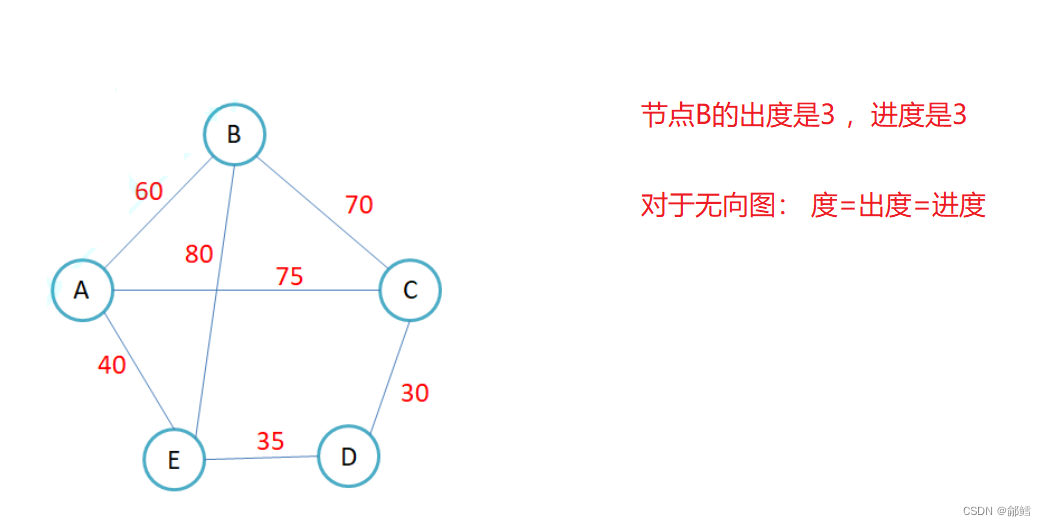
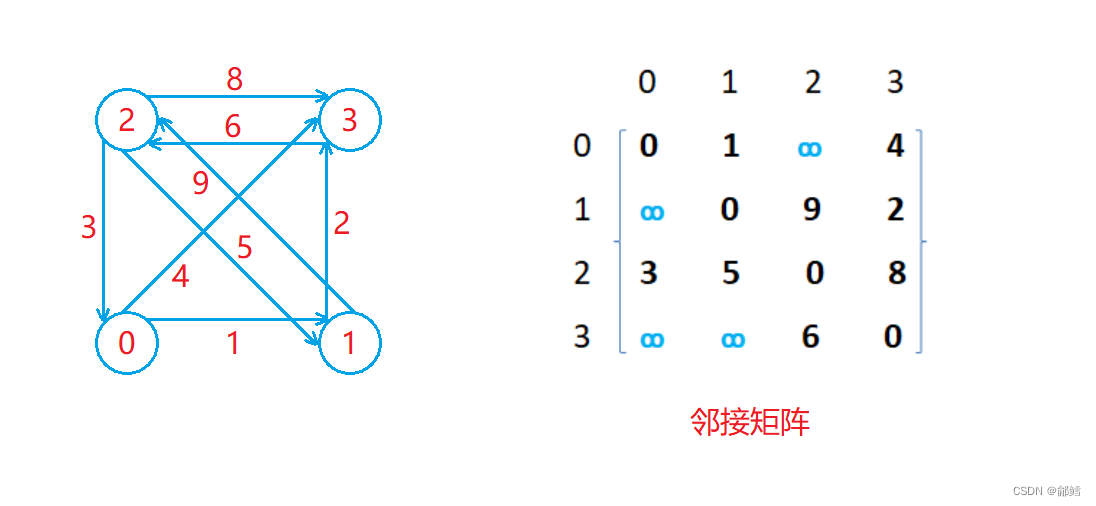
在这里插入图片描述

邻接矩阵

在这里插入图片描述

#pragma once 
#include<map>
#include<vector>
#include<algorithm>
#include<assert.h>
#include<string>
#include <functional>
#include<iostream>
using namespace std;
//矩阵 
namespace matrix
{//V是顶点 ，W是 weight 权值 template <class V, class W, W MAX_W = INT_MAX, bool Direction = false>  //true是有向图 ，false是无向图class Graph{public://手动添加边Graph(const V* a, size_t n)  //用指针数组 存储顶点{_vertex.reserve(n);//初始化顶点和边for (size_t i = 0; i < n; i++){_vertex.push_back(a[i]);_indexMap[a[i]] = i; //通过顶点找下标}_matrix.resize(n);for (size_t i = 0; i < n; i++){//将邻接矩阵的权值设置为最大值_matrix[i].resize(n, MAX_W);}}size_t  GetVertexIndexMap(const V& v){auto  it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else //没有找到 {assert(false);return -1;}}void AddEdge(const V& src, const V& dst, const W& w){int srci = GetVertexIndexMap(src);int dsti = GetVertexIndexMap(dst);_matrix[srci][dsti] = w;//无向图 if (Direction == false){_matrix[srci][dsti] = w;_matrix[dsti][srci] = w;}}void  Print(){//顶点 for (int i = 0; i < _vertex.size(); i++){cout << "[" << i << "]" << "->" << _vertex[i] << endl;}//矩阵 cout << endl;//打印横下标cout << "  ";for (size_t i = 0; i < _vertex.size(); i++){cout << i << " ";}cout << endl;for (int i = 0; i < _matrix.size(); i++){cout << i << " ";//打印竖下标for (int j = 0; j < _matrix[0].size(); j++){if (_matrix[i][j] == MAX_W){cout << "*"<<" ";}else{cout << _matrix[i][j] <<" ";}}cout << endl;}}public:vector<V> _vertex;  //顶点集合 map<V, int>  _indexMap;					//顶点映射下标 vector< vector<W> >	 _matrix;					//邻接矩阵};void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}
}

邻接表

邻接表：使用数组表示顶点的集合，使用链表表示边的关系

出边表：存储从各个顶点连接出去的边，出边表中下标为 i的位置存储的是从编号为i的顶点连接出去的边

入边表：存储连接到各个顶点的边，入边表中下标为i的位置存储的是连接到编号为 i的顶点的边
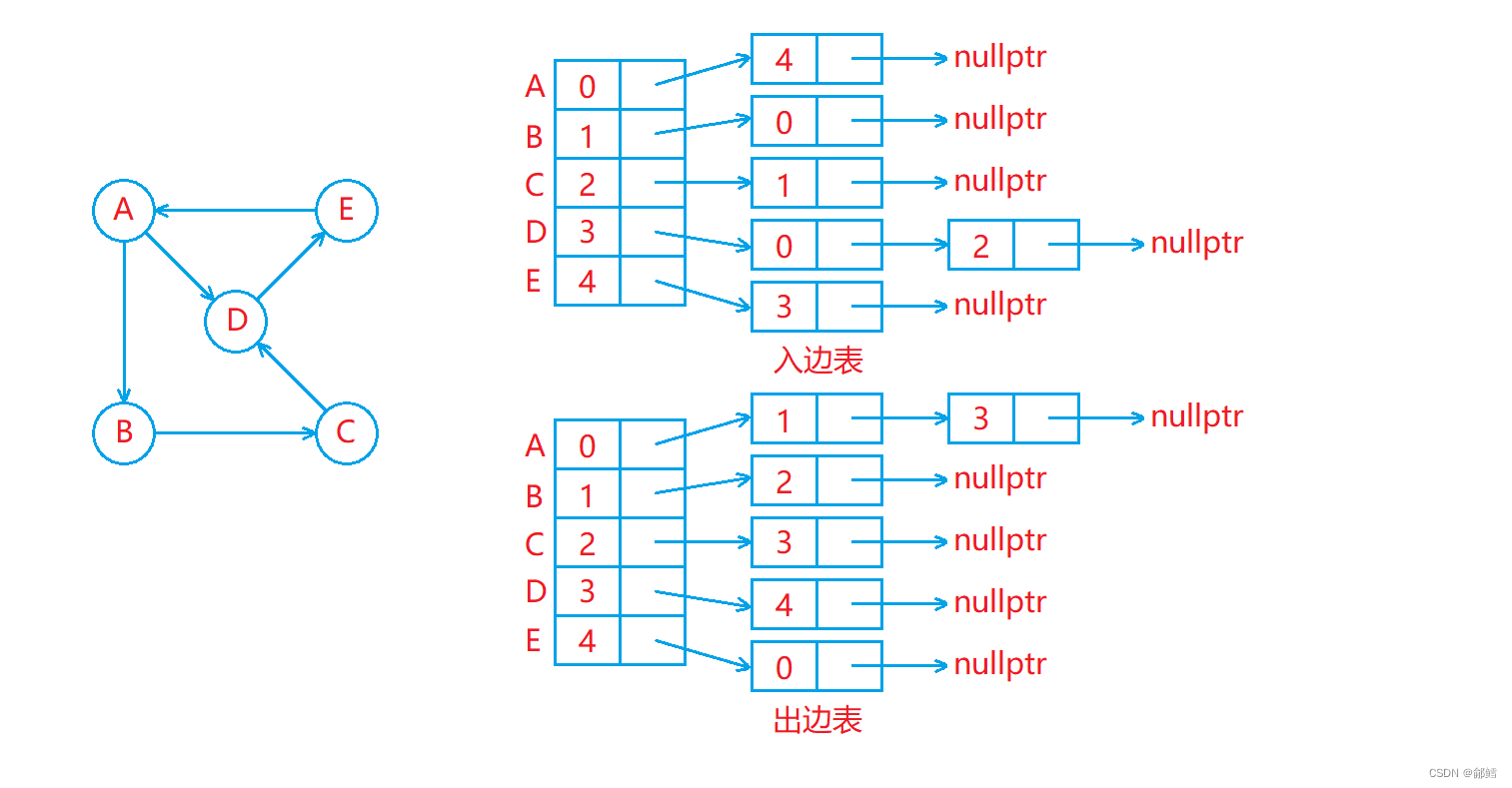
在这里插入图片描述
出边表和入边表的其中每个位置存储的都是一个链表
出边表中下标为i的位置表示从编号为i的顶点连接出去的边
入边表中下标为i 的位置表示连接到编号为i 的顶点的边

在实现邻接表时，一般只需要用一个出边表来存储从各个顶点连接出去的边即可，因为大多数情况下都是需要从一个顶点出发找与其相连的其他顶点，所以一般不需要存储入边表

//邻接表
namespace link_table
{template<class  W>struct Edge{int _dsti;//目标点的下标 W _w;//权值Edge<W> *_next; //用链表表示边的关系Edge(int dsti, const W& w):_dsti(dsti), _w(w), _next(nullptr)  {}};//V是顶点 ，W是 weight 权值 template <class V, class W, bool Direction = false>  //true是有向图 ，false是无向图class Graph{public:typedef Edge<W> Edge;//手动添加边Graph(const V* a, size_t n)  //用指针数组 存储顶点{_vertex.reserve(n);//初始化顶点和边for (size_t i = 0; i < n; i++){_vertex.push_back(a[i]);_indexMap[a[i]] = i; //通过顶点找下标}_table.resize(n, nullptr);}size_t  GetVertexIndexMap(const V& v){auto  it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else //没有找到 {assert(false);return -1;}}void AddEdge(const V& src, const V& dst, const W& w){int srci = GetVertexIndexMap(src); int dsti = GetVertexIndexMap(dst);//头插Edge *eg = new Edge(dsti,w);//有向图 //添加从源顶点到目标顶点的边eg->_next = _table[srci];_table[srci] = eg;//无向图 //添加从目标顶点到源顶点的边if (Direction == false){//????Edge* eg = new Edge(srci, w);eg->_next = _table[dsti];_table[dsti] = eg;}}void  Print(){//顶点 for (int i = 0; i < _vertex.size(); i++){cout << "[" << i << "]" << "->" << _vertex[i] << endl;}cout << endl;//遍历顶点for (size_t i = 0; i < _vertex.size(); i++){cout << _vertex[i] << endl;}//遍历邻接表的目标点的下标和权值 for (size_t i = 0; i < _table.size(); i++){cout << _vertex[i] << "[" << i << "]->";Edge * cur = _table[i];while (cur != nullptr){cout << "[" << _vertex[cur->_dsti] << ":" << cur->_dsti << ":" << cur->_w << "]->";cur = cur->_next;}cout << "nullptr" << endl;}}public:vector<V> _vertex;  //顶点集合 map<V, int>  _indexMap;					//顶点映射下标 vector<  Edge*>	 _table;					//邻接表};void TestGraph(){string a[] = { "张三", "李四", "王五", "赵六" };Graph<string, int, true> g1(a, 4);g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.Print();}
}

图的遍历

BFS

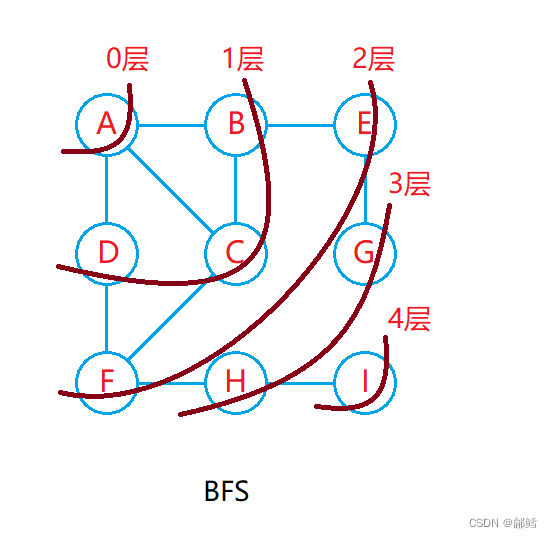
在这里插入图片描述

void BFS(const V& src)  //遍历顶点，通过下标找顶点{size_t srci = GetVertexIndexMap(src);queue<int>  q;vector<bool>  v(_vertex.size(), false);  //防止走重复的路q.push(srci);v[srci] = true;while (!q.empty()){int front = q.front();q.pop();cout << _vertex[front] << endl;// 把front顶点的邻接顶点的下标入队列for (size_t i = 0; i < _vertex.size(); i++){if (_matrix[front][i] != MAX_W && v[i] == false){q.push(i);v[i] = true;}}}}

DFS

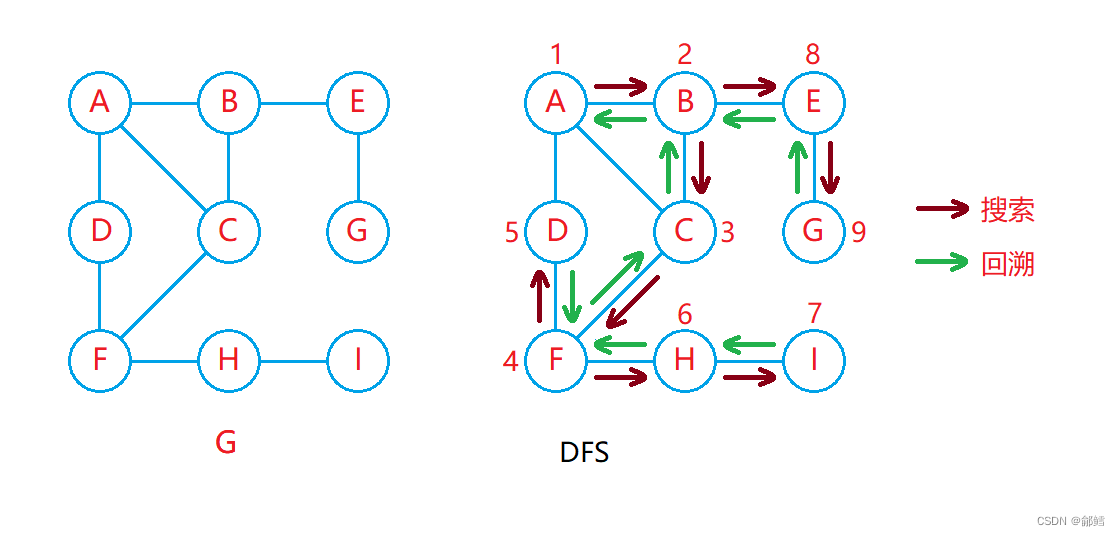
在这里插入图片描述

void _DFS(    size_t srci  ,vector<bool> & v){cout << srci << ":" << _vertex[srci] << endl;v[srci] = true;// 找一个srci相邻的没有访问过的点，去往深度遍历for (int i =0 ; i< _vertex.size()  ; i++ ){if (v[i] ==false && _matrix[srci][i] != MAX_W){_DFS(i ,v);}}}void  DFS(const V& src) //遍历顶点，通过下标找顶点{vector<bool>  v(_vertex.size(), false);  //防止走重复的路size_t  srci = GetVertexIndexMap(src);_DFS(srci, v);}

完整测试代码

#pragma once 
#include<map>
#include<vector>
#include<algorithm>
#include<assert.h>
#include<string>
#include <functional>
#include<iostream>
#include<queue>
using namespace std;
//矩阵 
namespace matrix
{//V是顶点 ，W是 weight 权值 //连通的,边的关系就用权值代替，如果两顶点不通，则使用无穷大代替template <class V, class W, W MAX_W = INT_MAX, bool Direction = false>  //true是有向图 ，false是无向图class Graph{public://手动添加边Graph(const V* a, size_t n)  //用指针数组 存储顶点{_vertex.reserve(n);//初始化顶点和边for (size_t i = 0; i < n; i++){_vertex.push_back(a[i]);_indexMap[a[i]] = i; //通过顶点找下标}_matrix.resize(n);for (size_t i = 0; i < n; i++){//将邻接矩阵的权值设置为最大值_matrix[i].resize(n, MAX_W);}}size_t  GetVertexIndexMap(const V& v){auto  it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else //没有找到 {assert(false);return -1;}}void AddEdge(const V& src, const V& dst, const W& w){int srci = GetVertexIndexMap(src);int dsti = GetVertexIndexMap(dst);_matrix[srci][dsti] = w;//无向图 if (Direction == false){_matrix[srci][dsti] = w;_matrix[dsti][srci] = w;}}void  Print(){//顶点 for (int i = 0; i < _vertex.size(); i++){cout << "[" << i << "]" << "->" << _vertex[i] << endl;}//矩阵 cout << endl;//打印横下标cout << "  ";for (size_t i = 0; i < _vertex.size(); i++){cout << i << " ";}cout << endl;for (int i = 0; i < _matrix.size(); i++){cout << i << " ";//打印竖下标for (int j = 0; j < _matrix[0].size(); j++){if (_matrix[i][j] == MAX_W){cout << "*"<<" ";}else{cout << _matrix[i][j] <<" ";}}cout << endl;}}void BFS(const V& src)  //遍历顶点，通过下标找顶点{size_t srci = GetVertexIndexMap(src);queue<int>  q;vector<bool>  v(_vertex.size(), false);  //防止走重复的路q.push(srci);v[srci] = true;while (!q.empty()){int front = q.front();q.pop();cout << _vertex[front] << endl;// 把front顶点的邻接顶点的下标入队列for (size_t i = 0; i < _vertex.size(); i++){if (_matrix[front][i] != MAX_W && v[i] == false){q.push(i);v[i] = true;}}}}void _DFS(    size_t srci  ,vector<bool> & v){cout << srci << ":" << _vertex[srci] << endl;v[srci] = true;// 找一个srci相邻的没有访问过的点，去往深度遍历for (int i =0 ; i< _vertex.size()  ; i++ ){if (v[i] ==false && _matrix[srci][i] != MAX_W){_DFS(i ,v);}}}void  DFS(const V& src) //遍历顶点，通过下标找顶点{vector<bool>  v(_vertex.size(), false);  //防止走重复的路size_t  srci = GetVertexIndexMap(src);_DFS(srci, v);}public:vector<V> _vertex;  //顶点集合 map<V, int>  _indexMap;					//顶点映射下标 vector< vector<W> >	 _matrix;					//邻接矩阵};void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}void TestBDFS(){string a[] = { "张三", "李四", "王五", "赵六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();//g1.BFS("张三");g1.DFS("张三");}
}//邻接表
namespace link_table
{template<class  W>struct Edge{int _dsti;//目标点的下标 W _w;//权值Edge<W> *_next; //用链表表示边的关系Edge(int dsti, const W& w):_dsti(dsti), _w(w), _next(nullptr)  {}};//V是顶点 ，W是 weight 权值 template <class V, class W, bool Direction = false>  //true是有向图 ，false是无向图class Graph{public:typedef Edge<W> Edge;//手动添加边Graph(const V* a, size_t n)  //用指针数组 存储顶点{_vertex.reserve(n);//初始化顶点和边for (size_t i = 0; i < n; i++){_vertex.push_back(a[i]);_indexMap[a[i]] = i; //通过顶点找下标}_table.resize(n, nullptr);}size_t  GetVertexIndexMap(const V& v){auto  it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else //没有找到 {assert(false);return -1;}}void AddEdge(const V& src, const V& dst, const W& w){int srci = GetVertexIndexMap(src); int dsti = GetVertexIndexMap(dst);//头插Edge *eg = new Edge(dsti,w);//有向图 //添加从源顶点到目标顶点的边eg->_next = _table[srci];_table[srci] = eg;//无向图 //添加从目标顶点到源顶点的边if (Direction == false){//????Edge* eg = new Edge(srci, w);eg->_next = _table[dsti];_table[dsti] = eg;}}void  Print(){//顶点 for (int i = 0; i < _vertex.size(); i++){cout << "[" << i << "]" << "->" << _vertex[i] << endl;}cout << endl;//遍历顶点for (size_t i = 0; i < _vertex.size(); i++){cout << _vertex[i] << endl;}//遍历邻接表的目标点的下标和权值 for (size_t i = 0; i < _table.size(); i++){cout << _vertex[i] << "[" << i << "]->";Edge * cur = _table[i];while (cur != nullptr){cout << "[" << _vertex[cur->_dsti] << ":" << cur->_dsti << ":" << cur->_w << "]->";cur = cur->_next;}cout << "nullptr" << endl;}}public:vector<V> _vertex;  //顶点集合 map<V, int>  _indexMap;					//顶点映射下标 vector<  Edge*>	 _table;					//邻接表};void TestGraph(){string a[] = { "张三", "李四", "王五", "赵六" };Graph<string, int, true> g1(a, 4);g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.Print();}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/274996.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

考研C语言复习进阶（1）

考研C语言复习进阶（1）

目录 1. 数据类型介绍 1.1 类型的基本归类&#xff1a; 2. 整形在内存中的存储 2.1 原码、反码、补码 2.2 大小端介绍 3. 浮点型在内存中的存储 ​编辑 1. 数据类型介绍 前面我们已经学习了基本的内置类型&#xff1a; char //字符数据类型 short //短整型 int /…
阅读更多...
【Python】random库

【Python】random库

专栏文章索引&#xff1a;Python 原文章&#xff1a;Python中random函数用法整理_python random-CSDN博客 目录 1.random.random() 2.random.uniform(a, b) 3.random.randint(a, b) 4.random.randrange([start], stop[, step]) 5. random.choice() 6. random.shuffle(x[,…
阅读更多...
测试用例的设计(2)

测试用例的设计(2)

目录 1.前言 2.正交排列(正交表) 2.1什么是正交表 2.2正交表的例子 2.3正交表的两个重要性质 3.如何构造一个正交表 3.1下载工具 3.1构造前提 4.场景设计法 5.错误猜测法 1.前言 我们在前面的文章里讲了测试用例的几种设计方法,分别是等价类发,把测试例子划分成不同的类…
阅读更多...
鸿蒙开发面试真题分享~

鸿蒙开发面试真题分享~

1. 在鸿蒙应用开发中&#xff0c;有哪些常用的性能优化策略和技术手段&#xff0c;如启动速度优化、内存管理优化、功耗控制等&#xff1f; 参考答案&#xff1a; 2. 鸿蒙系统强调跨平台特性&#xff0c;你会如何利用这一特性来优化多端部署和适配&#xff1f; 参考答案&…
阅读更多...
关于Spark中OptimizeShuffleWithLocalRead 中自己的一些理解

关于Spark中OptimizeShuffleWithLocalRead 中自己的一些理解

背景 本文基于 Spark 3.5 关于ShuffleLocalRead的作用简单的来说&#xff0c;就是会按照一定的规则&#xff0c;从一个 map Task 中连续读取多个 reduce数据 的任务&#xff0c;&#xff08;正常的情况下是读取所有map Task中特定的一个reduce数据任务&#xff09;&#xff0c…
阅读更多...
DJI RONIN 4D变0字节恢复案例

DJI RONIN 4D变0字节恢复案例

RONIN 4D这个产品听起来比较陌生&#xff0c;还是DJI大疆出品。没错&#xff0c;这是大疆进军影视级的重点明星机型。前阵子刚处理过大疆RONIN 4D的修复案例&#xff0c;下边这个案例是和exfat有关的老问题:文件长度变成0字节。 故障存储:希捷18T /MS Exfat文件系统。 故障现…
阅读更多...
海豚调度系列之：任务类型——SPARK节点

海豚调度系列之：任务类型——SPARK节点

海豚调度系列之&#xff1a;任务类型——SPARK节点 一、SPARK节点二、创建任务三、任务参数四、任务样例1.spark submit2.spark sql 五、注意事项&#xff1a; 一、SPARK节点 Spark 任务类型用于执行 Spark 应用。对于 Spark 节点&#xff0c;worker 支持两个不同类型的 spark…
阅读更多...
Orange3数据预处理(离散化组件)

Orange3数据预处理(离散化组件)

离散化&#xff1a;将数值属性转换为分类属性。 输出 数据&#xff1a;具有离散化值的数据集 设置离散化的默认方法。 选择变量以为每个变量设置特定的离散化方法。将鼠标悬停在变量上显示区间。 离散化方法Keep numeric(保持数值)&#xff1a;保持变量不变。Remove (移除)&a…
阅读更多...
介绍第一位 AI 软件工程师 Devin

介绍第一位 AI 软件工程师 Devin

认识 Devin&#xff0c;世界上第一位完全自主的 AI 软件工程师。 ‍ Devin 是一位孜孜不倦、技术娴熟的队友&#xff0c;同样愿意与您一起构建或独立完成任务供您查看。 有了 Devin&#xff0c;工程师可以专注于更有趣的问题&#xff0c;工程团队可以为更雄心勃勃的目标而奋斗。…
阅读更多...
如何利用生成式人工智能撰写英语商务邮件？

如何利用生成式人工智能撰写英语商务邮件？

写商务邮件简介 在当今数字化时代&#xff0c;能够撰写有效的商务邮件是一项无价的技能。电子邮件是专业世界中主要的沟通方式&#xff0c;在轻松跨越距离和时区的同时&#xff0c;也带来了一系列挑战&#xff1b;它要求清晰、高效&#xff0c;并遵循某些专业礼仪的潜在规则。…
阅读更多...
常用的gpt网站

常用的gpt网站

ChatGPT是一款基于人工智能技术的对话型AI助手&#xff0c;能够进行自然语言交互并提供个性化的对话服务。通过先进的深度学习模型&#xff0c;ChatGPT能够理解用户输入的文本&#xff0c;并生成有逻辑、连贯性的回复。它可以回答各种问题、提供建议、分享知识&#xff0c;还能…
阅读更多...
2024年软考计划开始了，你准备好了吗？

2024年软考计划开始了，你准备好了吗？

目录标题 2024年度计算机技术与软件专业技术资格&#xff08;水平&#xff09;考试工作计划计算机软考中级科目哪个含金量最高&#xff1f;报考流程和说明 2024年度计算机技术与软件专业技术资格&#xff08;水平&#xff09;考试工作计划 一、2024年度计算机软件资格考试(初级…
阅读更多...
SSM整合和实战练习笔记

SSM整合和实战练习笔记

SSM整合和实战练习1 SSM整合springmvc配置业务层 service aop tx的配置mybatis整合配置&#xff08;方式2容器初始化配置类访问测试mapper层service层controller层 实战练习前端程序搭建后端程序搭建配置类创建实体类三层架构搭建(controller service mapper)功能实现&#xff…
阅读更多...
Java学习笔记（7）

Java学习笔记（7）

练习 package exercise3;public class FightTest {public static void main(String[] args) {Role r1 new Role("kobe", 100);Role r2 new Role("james", 100);while (true) {r1.attack(r2);if (isWin(r1,r2)) break;r2.attack(r1);if (isWin(r2,r1)) br…
阅读更多...
虚幻4 | 制作游戏——学习记录（一）

虚幻4 | 制作游戏——学习记录（一）

1. 启动Epic后下载虚幻4&#xff0c;打开虚幻4后新建一个第三人称游戏项目&#xff0c;效果如下&#xff1a; &#xff08;1&#xff09;内容/ThirdPersonBP/Blueprints中的ThirdPersonCharacter&#xff08;左下角人物&#xff09; 这是模板中使用的主要蓝图类&#xff0c;它…
阅读更多...
Frostmourne - Elasticsearch源日志告警配置

Frostmourne - Elasticsearch源日志告警配置

简介 配置Frostmourne 接入Elasticsearch源进行日志匹配告警&#xff0c;并静默规则&#xff0c;告警消息发送到企业微信&#xff0c;告警信息使用Markdown。 部署安装教程查看&#xff1a; https://songxwn.com/frostmourne_install ELK 安装教程&#xff1a;https://songx…
阅读更多...
【Android】 ClassLoader 知识点提炼

【Android】 ClassLoader 知识点提炼

1.Java中的 ClassLoader 1.1 、ClassLoader的类型 Java 中的类加载器主要有两种类型&#xff0c;即系统类加载器和自定义类加载器。其中系统类 加载器包括3种&#xff0c;分别是 Bootstrap ClassLoader、Extensions ClassLoader 和 Application ClassLoader。 1.1.1.Bootstra…
阅读更多...
从0到1入门C++编程——12 演讲比赛流程管理系统

从0到1入门C++编程——12 演讲比赛流程管理系统

文章目录 一、创建类并显示菜单二、退出管理系统三、开始演讲比赛四、查看往届记录五、清空比赛记录六、案例源代码 演讲比赛流程管理系统 比赛规则&#xff1a;演讲比赛共有12个人参加&#xff0c;比赛分两轮进行&#xff0c;第一轮为淘汰赛&#xff0c;第二轮为决赛。每名选手…
阅读更多...
Java中 final、finally、finalize 有什么区别？

Java中 final、finally、finalize 有什么区别？

1、典型回答 final、finally、finalize 是 Java 中三个不同的关键字&#xff0c;它们除了长得像之外&#xff0c;其他的&#xff08;作用和含义&#xff09;完全不同。 它们三个的区别就好像&#xff1a;雷、雷锋、雷峰塔之间的区别。&#xff08;是三个完全不同的东西&#…
阅读更多...
STM32---通用定时器（一）理论基础

STM32---通用定时器（一）理论基础

写在前面&#xff1a;在STM32F103中有众多的定时器&#xff0c;其中包括两个基本定时器&#xff0c;基本定时器的内容已经在上节进行了介绍&#xff0c;基本定时器的功能、结构、使用都较为简单。而STM32F1中还含有4个通用定时器&#xff08;TIM2\3\4\5&#xff09;,这些定时器…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023