【数据结构】二叉树---AVL树的实现

      

目录

一.  什么是AVL树

二.  AVL树的结点结构定义

三.  AVL树的动态平衡法

1. 左单旋转 --- RL(RotateLeft) 型调整操作

2. 右单旋转 --- RR(RotateRight) 型调整操作

3. 先左后右双旋转 --- RLR (RotateLeftRight) 型调整操作

4. 先右后左双旋转 --- RRL (RotateRightLeft) 型调整操作

四.  AVL树的插入操作

五.  AVL树的验证操作

六.  完整源代码

一.  什么是AVL树

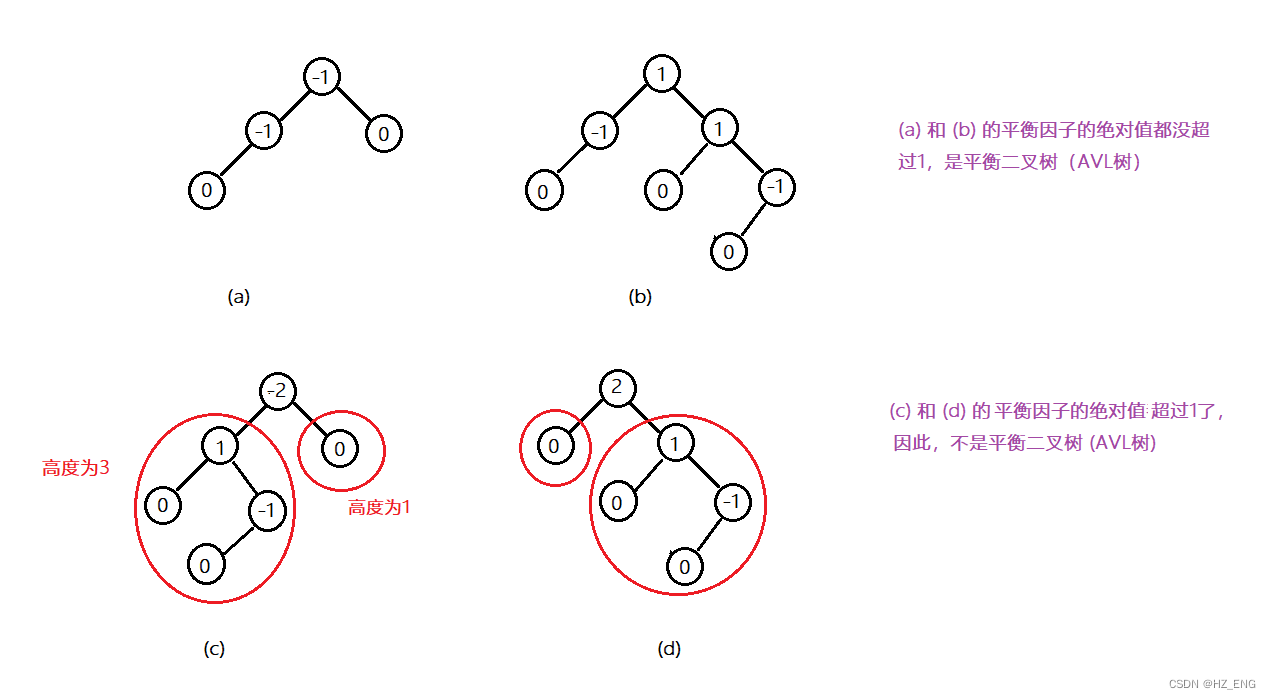
AVL树，又称平衡二叉树。   

       它可以是一颗空树，或者是具有以下性质的二叉树：即它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度只差的绝对值不超过 1。 把二叉树上结点的平衡因子BF定义为该结点的左子树的高度和右子树的高度之差（即平衡二叉树上结点的平衡因子只可能是 -1、0 和 1）

       只要二叉树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。

   说明：后面所用到的平衡因子的都是右子树的高的 - 左子树的高度

二.  AVL树的结点结构定义

       影响二叉搜索树平衡的操作只能是插入和删除，这里已插入为例，同样一组数据元素插  入的顺序不同，二叉搜索树的形状就不同。也就需要一种动态平衡方法，当插入操作破坏了平衡，便可以用来调整。这种方式需要在原来二叉搜索树结点中增加一个量为平衡因子(BF)

结点结构图：

在这里为了方便进行旋转操作对于AVL树的结点定义采用三叉链的结构：

//类模板结点的定义
template <class T>
struct AVLTreeNode
{AVLTreeNode<T>* _left;AVLTreeNode<T>* _right;AVLTreeNode<T>* _parent;   //指向当前结点的父节点的指针AVLTreeNode<T> _data;int _bf;                      //平衡因子//结点的构造函数AVLTreeNode(const T& data):_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0),_data(data){}};

三.  AVL树的动态平衡法

        如果在一棵原本是平衡的AVL树中插入一个新节点，可能造成不平衡，此时必须调整树的结构， 使之平衡化。根据节点插入位置的不同，AVL树的旋转分为以下四种：

1. 左单旋转 --- RL(RotateLeft) 型调整操作

      单向左旋平衡处理: 由于在subR这个结点的右子树上插入结点 ，subR的平衡因子由0变为1，p的平衡因子由1变为2，导致以p为根的子树失去平衡，则需进行一次向左的逆时针旋转操作

    链接操作：b链接到p的右；

                      p链接到subR的左；

                      subR成为当前树的根

注意：1. 链接时subRL为空的情况

           2. p可能是整棵树的子树 (p的上面可能还有结点) 或 整棵树的根 (p的上面无结点)

图示：

    //左单旋转void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//做左旋转（修改结点的指向）parent->_right = subRL;if (subRL)                  //若subRL不为空，则修改subRL中指向父节点的指针(_parent)subRL->_parent = parent;subR->_left = parent;//修改各结点中父指针(_parent)的指向Node* ppnode = parent->_parent;         //保存parent中父指针(_parent)的指向parent->_parent = subR;                 //修改parent中指向父节点的指针(_parent)if (parent == _root)                    //判断当前结点是否为根节点{_root = subR;subR->_parent = nullptr;}else{if (ppnode->_right == parent){ppnode->_right = subR;}else{ppnode->_left = subR;}subR->_parent = ppnode;}//更新平衡因子parent->_bf = 0;subR->_bf = 0;}

2. 右单旋转 --- RR(RotateRight) 型调整操作

  单向右旋平衡处理: 由于在subL的左子树上插入结点，subL的平衡因子由 0变成 -1 ，p的平衡因子由 1 变为 -2，导致以p为根的子树失去平衡，则需进行一次向右的顺时针旋转操作。

   链接操作：b链接到p的左；

                     p链接到subL的右；

                     subL成为当前树的根

注意：1. 链接时subLR为空的情况

           2. p可能是整棵树的子树 (p的上面可能还有结点) 或 整棵树的根 (p的上面无结点)

图示：

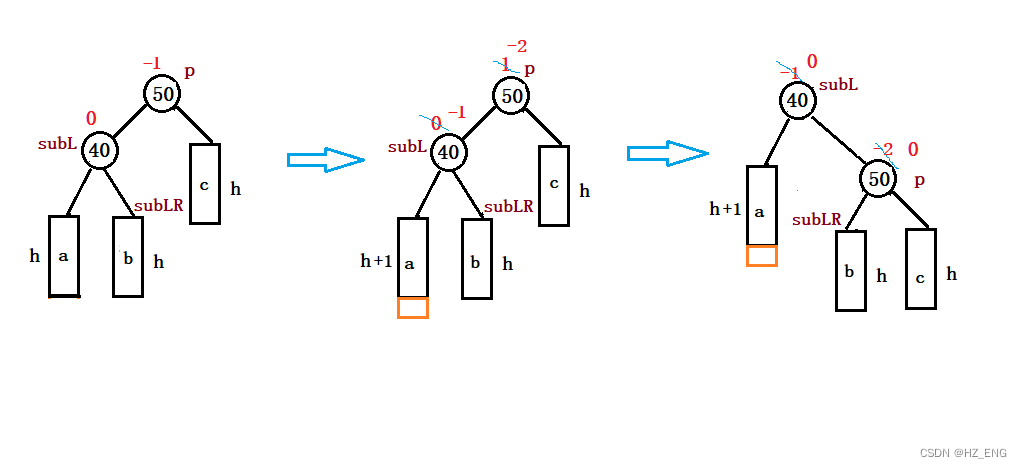
	//右单旋转void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;//做右旋转（修改结点的指向）parent->_left = subLR;if (subLR)                  //若subLR不为空，则修改subLR中指向父节点的指针(_parent)subLR->_parent = parent;subL->_right = parent;//修改各结点中父指针(_parent)的指向Node* ppnode = parent->_parent;     //保存parent中父指针(_parent)的指向parent->_parent = subL;             //修改parent中指向父节点的指针(_parent)if (parent == _root)                //判断当前结点是否为根节点{_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}//更改平衡因子parent->_bf = 0;subL->_bf = 0;}

3. 先左后右双旋转 --- RLR (RotateLeftRight) 型调整操作

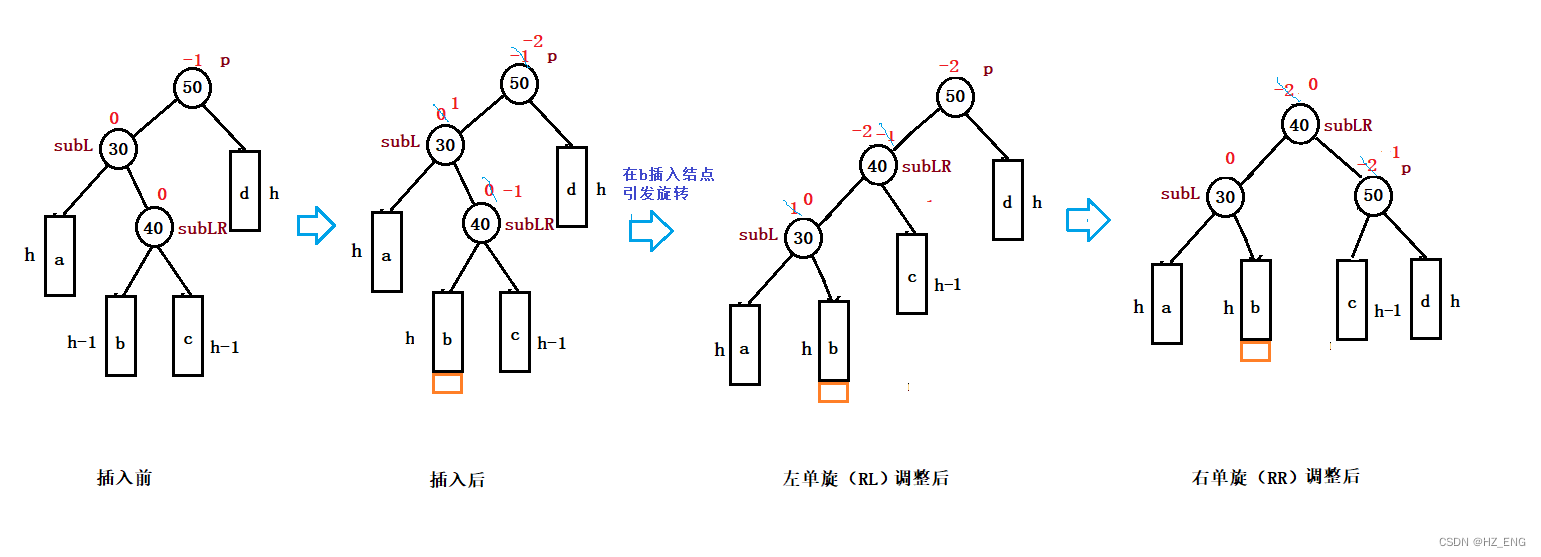
  双向旋转(先左后右)平衡处理：由于在subL的右子树上插入结点，subL的平衡因子由 0 变为 1，p的平衡因子由 -1 变为 -2，导致以p为根的子树失去平衡，则需进行两次旋转(先左旋后右旋)操作

   链接操作：左单旋：b链接到subL的右；

                                    subL链接到subLR的左；

                                    subLR链接到p的左

                      右单旋：c链接到p的左；

                                     p链接到subLR的右；

                                     subLR成为当前子树的根

图示：

    //先左后右双旋转void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;    //先保存旋转前subLR结点的平衡因子RotateL(parent->_left); //左单旋转RotateR(parent);        //右单旋转//更新旋转后的平衡因子if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}}

4. 先右后左双旋转 --- RRL (RotateRightLeft) 型调整操作

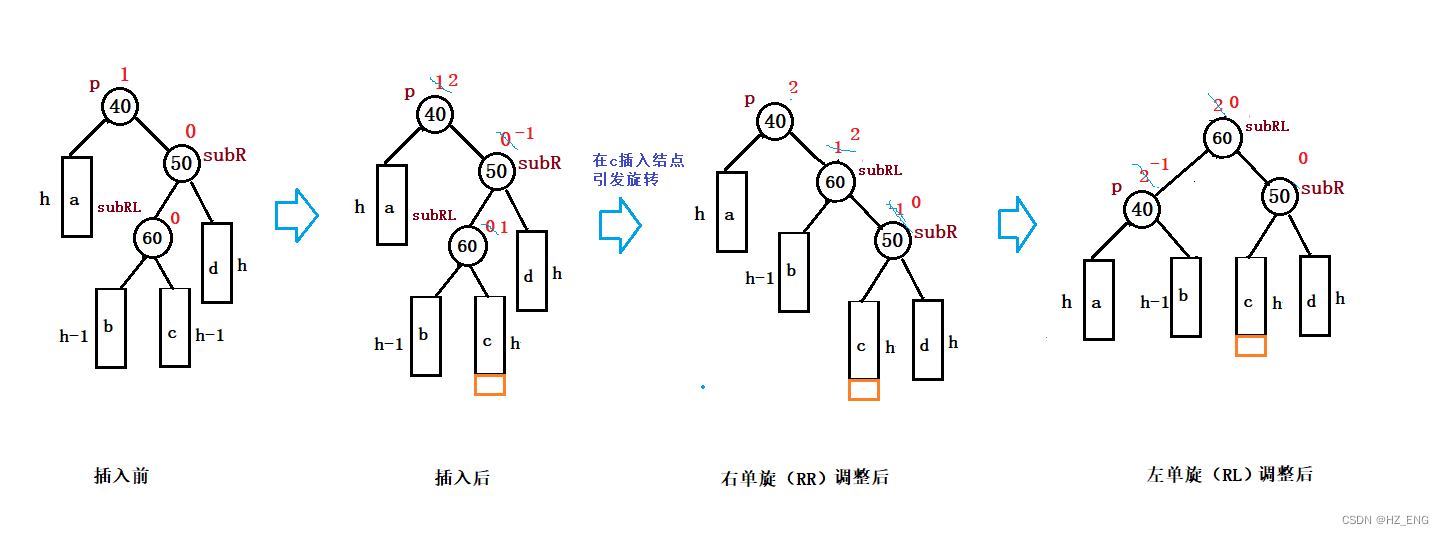
  双向旋转(先右后左)平衡处理：由于在subR的左子树上插入结点，subR的平衡因子由 0 变为 -1，p的平衡因子由 1 变为 2，导致以p为根的子树失去平衡，则需进行两次旋转(先右旋后左旋)操作

   链接操作：右单旋：c链接到subR的左；

                                    subR链接到subRL的右；

                                    subRL链接到p的右

                     左单旋：b链接到p的右；

                                    p链接到subRL的左；

                                    subRL成为当前子树的根

     

图示：

    //先右后左双旋转void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;    //先保存旋转前subRL结点的平衡因子            RotateR(subR);          //右单旋转RotateL(parent);        //左单旋转//更新旋转后的平衡因子if (bf == 1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;parent->_bf = 0;}else if(bf==0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}}

四.  AVL树的插入操作

        AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么 AVL树的插入过程可以分为两步：

       1. 按照二叉搜索树的方式插入新节点

       2. 调整节点的平衡因子      

        插入一个结点cur(当前要插入的结点)后，Parent的平衡因子一定需要调整，在插入之前，Parent 的平衡因子分为三种情况：-1，0, 1;

分以下两种情况：  

      1. 如果cur插入到Parent的左侧，只需给 Parent 的平衡因子 减1 即可  

      2. 如果cur插入到Parent的右侧，只需给 Parent 的平衡因子 加1 即可  

此时：Parent的平衡因子可能有三种情况：0，1或-1， 2或-2  

      1. 如果Parent的平衡因子为 0，说明插入之前Parent的平衡因子为 1或-1，插入后被调整成 0，此时满足 AVL树的性质，插入成功  

      2. 如果Parent的平衡因子为 1或-1，说明插入前Parent的平衡因子一定为 0，插入后被更新成 1或-1，此时，以Parent为根的树的高度增加，需要继续向上更新  

      3. 如果Parent的平衡因子为 2或-2，则Parent的平衡因子违反平衡树的性质，需要对其进行旋转处理

bool Insert(const T& data)
{//为空树if (_root == nullptr){_root = new Node(data);return true;}//按照二叉搜索树的规则插入结点Node* parent = nullptr;  //记录插入结点的父节点Node* cur = _root;while (cur){if (cur->_data < data){parent = cur;cur = cur->_right;}else if (cur->_data > data){parent = cur;cur = cur->_left;}else{return false;}}//判断链接到父节点的那边cur = new Node(data);if (parent->_data > data){parent->_left = cur;}else{parent->_right = cur;}//调整平衡因子 及 旋转调整 cur->_parent = parent; //修改当前结点(cur)的父指针（_parent）的指向while (parent){if (cur == parent->_left) //插入到父结点的左边，父节点的平衡因子--{parent->_bf--;}else                 //插入到父结点的左边，父节点的平衡因子--{parent->_bf++;}//if (parent->_bf == 0)   //若（插入节点后）当前结点的平衡因子为零，则不会影响此节点的父及祖先结点；{                       //说明当前这颗子树插入节点后，其高度没有发生变化，也就不需要向上更新平衡因子break;}else if (parent->_bf == 1 || parent->_bf == -1)  //若当前结点的平衡因子为1或-1，则会影响上面的祖先结点的平衡因子{											     //需要更新上面祖先的平衡因子cur = cur->_parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)//若当前结点的平衡因子为2或-2,则需做旋转调整{//旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent); //左单旋转}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent); //右单旋转}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent); //先左单旋转，在右单旋转}else{RotateRL(parent); //先右单旋转，在左单旋转}break;}else            //说明插入之前AVL数就有问题{assert(false);}}return true;
}

五.  AVL树的验证操作

AVL树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证AVL树，可以分两步：

     1. 验证其为二叉搜索树 如果中序遍历可得到一个有序的序列，就说明为二叉搜索树

            验证方法：采用中序遍历即可

     2. 验证其为平衡树 每个节点子树高度差的绝对值不超过1

         (注意节点中如果没有平衡因子) 节点的平衡因子是否计算正确

            验证方法：1.验证每颗子树的左右高度差的绝对值是否超过 1（采用递归思想）；

                              2.验证结点的平衡因子是否正确

    //中序遍历void InOrder(Node* root){if (root == nullptr)return;InOrder(root->_left);cout << root->_data << endl;InOrder(root->_right);}//求树的高度int _Height(Node* root){if (root == nullptr)return 0;int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;}// 验证AVL树的平衡bool _IsAVLTree1(Node* root) //前序遍历 {if (root == nullptr)return true;int leftheight = _Height(root->_left);  //左子树的高度int rightheight = _Height(root->_right); //右子树的高度//判断左右高度差是否超过1if (abs(rightheight - leftheight) >= 2){cout << root->_data << "不平衡" << endl;return false;}//判断结点的平衡因子是否有异常	if (rightheight - leftheight != root->_bf){cout << root->_data << "平衡因子异常" << endl;return false;}return _IsAVLTree1(root->_left) && _IsAVLTree1(root->_right);}

六.  完整源代码

template <class T>
struct AVLTreeNode
{AVLTreeNode<T>* _left;AVLTreeNode<T>* _right;AVLTreeNode<T>* _parent;   //指向当前结点的父节点的int _bf;                      //平衡因子T _data;AVLTreeNode(const T& data):_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0),_data(data){}};template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public:AVLTree(): _root(nullptr){}bool Insert(const T& data){if (_root == nullptr){_root = new Node(data);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_data < data){parent = cur;cur = cur->_right;}else if (cur->_data > data){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data);if (parent->_data > data){parent->_left = cur;}else{parent->_right = cur;}//调整平衡因子 及 旋转调整 cur->_parent = parent; while (parent){if (cur == parent->_left) //插入到父结点的左边，父节点的平衡因子--{parent->_bf--;}else                 //插入到父结点的左边，父节点的平衡因子--{parent->_bf++;}if (parent->_bf == 0)   {                       break;}else if (parent->_bf == 1 || parent->_bf == -1) {											     //需要更新上面祖先的平衡因子cur = cur->_parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent); //左单旋转}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent); //右单旋转}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent); //先左单旋转，在右单旋转}else{RotateRL(parent); //先右单旋转，在左单旋转}break;}else            //说明插入之前AVL数就有问题{assert(false);}}return true;}//左单旋转void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//做左旋转（修改结点的指向）parent->_right = subRL;if (subRL)                  //若subRL不为空，则修改subRL中指向父节点的指针(_parent)subRL->_parent = parent;subR->_left = parent;//修改各结点中父指针(_parent)的指向Node* ppnode = parent->_parent;         //保存parent中父指针(_parent)的指向parent->_parent = subR;                 //修改parent中指向父节点的指针(_parent)if (parent == _root)                    //判断当前结点是否为根节点{_root = subR;subR->_parent = nullptr;}else{if (ppnode->_right == parent){ppnode->_right = subR;}else{ppnode->_left = subR;}subR->_parent = ppnode;}//更新平衡因子parent->_bf = 0;subR->_bf = 0;}//右单旋转void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;//做右旋转（修改结点的指向）parent->_left = subLR;if (subLR)                  //若subLR不为空，则修改subLR中指向父节点的指针(_parent)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;   parent->_parent = subL;             if (parent == _root)              {_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}//更改平衡因子parent->_bf = 0;subL->_bf = 0;}//先左后右双旋转void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;    RotateL(parent->_left); RotateR(parent);        //更新旋转后的平衡因子if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}}//先右后左双旋转void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;    RotateR(subR); RotateL(parent);   //更新旋转后的平衡因子if (bf == 1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;parent->_bf = 0;}else if(bf==0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}}//高度int Height(){return _Height(_root);}// AVL树的验证bool IsAVLTree(){return _IsAVLTree1(_root);}//中序遍历void InOrder(){_InOrder(_root);}private:int _Height(Node* root){if (root == nullptr)return 0;int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;}// AVL树的验证bool _IsAVLTree1(Node* root) //前序遍历 {if (root == nullptr)return true;int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);if (abs(rightheight - leftheight) >= 2){cout << root->_data << "不平衡" << endl;return false;}if (rightheight - leftheight != root->_bf){cout << root->_data << "平衡因子异常" << endl;return false;}return _IsAVLTree1(root->_left) && _IsAVLTree1(root->_right);}//中序遍历void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_data << endl;_InOrder(root->_right);}private:Node* _root;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/275560.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Day32：安全开发-JavaEE应用Servlet路由技术JDBCMybatis数据库生命周期

Day32：安全开发-JavaEE应用Servlet路由技术JDBCMybatis数据库生命周期

目录 JavaEE-HTTP-Servlet&路由&周期 JavaEE-数据库-JDBC&Mybatis&库 思维导图 Java知识点&#xff1a; 功能&#xff1a;数据库操作&#xff0c;文件操作&#xff0c;序列化数据&#xff0c;身份验证&#xff0c;框架开发&#xff0c;第三方库使用等. 框架…
阅读更多...
最新若依项目快速上手

最新若依项目快速上手

最新若依项目快速上手 配套视频&#xff1a;若依项目快速上手视频 1. 下载源码 官网&#xff1a;https://ruoyi.vip/ 前端 git clone https://github.com/yangzongzhuan/RuoYi-Vue3.git后端 git clone https://gitee.com/y_project/RuoYi-Vue.git2. 数据库 创建数据库ry-vue…
阅读更多...
考研复习C语言初阶（3）

考研复习C语言初阶（3）

目录 一.函数是什么? 二.C语言中函数的分类 2.1库函数 2.2自定义函数 三.函数的参数 3.1实际参数&#xff08;实参&#xff09; 3.2 形式参数&#xff08;形参&#xff09; 四.函数的调用 4.1 传值调用 4.2 传址调用 五. 函数的嵌套调用和链式访问 5.1 嵌套调用 5…
阅读更多...
Android中单例模式正确实现方式

Android中单例模式正确实现方式

1. 饿汉模式 -线程安全 在类加载时进行实例化&#xff0c; 线程安全&#xff0c;但会导致类加载时间变长。饿汉模式如果使用过多&#xff0c;可能会对App启动耗时带来不利影响。 2. 懒汉模式 -线程不安全 没有加锁&#xff0c; 因此线程不安全。 3. 两次判空 加同步锁 -线程不…
阅读更多...
Talk｜麻省理工学院李晨昊：发展式腿足智能-从模仿到生成

Talk｜麻省理工学院李晨昊：发展式腿足智能-从模仿到生成

本期为TechBeat人工智能社区第578期线上Talk。 北京时间3月13日(周三)20:00&#xff0c;麻省理工学院博士生—李晨昊的Talk已准时在TechBeat人工智能社区开播&#xff01; 他与大家分享的主题是: “发展式腿足智能-从模仿到生成”&#xff0c;向大家系统地介绍了专家示范(exper…
阅读更多...
基于四边形网格的服装设计

基于四边形网格的服装设计

前言 该篇论文对算法的描述是比较详细的&#xff0c;在Unity中复现其功能。我这边的效果是这样的。 不尽人意 正文开始 Sketch-Based Garment Design with Quad Meshes 基于草图的服装设计与四边形网格 2020/02/13 Jackdos整理翻译 Abstract摘要 Garment creation cont…
阅读更多...
ORACLE Linux(OEL) - Primavera P6EPPM 安装及分享

ORACLE Linux(OEL) - Primavera P6EPPM 安装及分享

引言 继上一期发布的CentOS版环境发布之后&#xff0c;近日我制作了基于ORACLE Linux的P6虚拟机环境&#xff0c;同样里面包含了全套P6 最新版应用服务 此虚拟机仅用于演示、培训和测试目的。如您在生产环境中使用此虚拟机&#xff0c;请先与Oracle Primavera销售代表取得联系…
阅读更多...
（黑马出品_高级篇_03）SpringCloud+RabbitMQ+Docker+Redis+搜索+分布式

（黑马出品_高级篇_03）SpringCloud+RabbitMQ+Docker+Redis+搜索+分布式

&#xff08;黑马出品_高级篇_03&#xff09;SpringCloudRabbitMQDockerRedis搜索分布式 微服务技术——多级缓存 今日目标1.什么是多级缓存2.JVM进程缓存2.1.导入案例2.1.1.安装MySQL2.1.1.1.准备目录2.1.1.2.运行命令2.1.1.3.修改配置 2.1.1.4.…
阅读更多...
C++提高笔记（三）---STL容器（vector、deque）

C++提高笔记（三）---STL容器（vector、deque）

1、vector容器 1.1vector基本概念 功能&#xff1a;vector数据结构和数组非常相似&#xff0c;也称为单端数组 vector与普通数组区别&#xff1a;不同之处在于数组是静态空间&#xff0c;而vector可以动态扩展 动态扩展&#xff1a;并不是在原空间之后续接新空间&#xff0…
阅读更多...
Day31：安全开发-JS应用WebPack打包器第三方库JQuery安装使用安全检测

Day31：安全开发-JS应用WebPack打包器第三方库JQuery安装使用安全检测

目录 打包器-WebPack-使用&安全 第三方库-JQuery-使用&安全 思维导图 JS知识点&#xff1a; 功能&#xff1a;登录验证&#xff0c;文件操作&#xff0c;SQL操作&#xff0c;云应用接入&#xff0c;框架开发&#xff0c;打包器使用等 技术&#xff1a;原生开发&…
阅读更多...
qt 格式化打印 日志 QMessagePattern 格式词法语法及设置

qt 格式化打印 日志 QMessagePattern 格式词法语法及设置

一、qt源码格式化日志 关键内部类 QMessagePattern qt为 格式化打印日志 提供了一个简易的 pattern(模式/格式) 词法解析的简易的内部类QMessagePattern，作用是获取和解析自定义的日志格式信息。 该类在qt的专门精心日志操作的源码文件Src\qtbase\src\corelib\global\qloggi…
阅读更多...
Seata源码流程图

Seata源码流程图

1.第一阶段分支事务的注册 流程图地址&#xff1a;https://www.processon.com/view/link/6108de4be401fd6714ba761d 2.第一阶段开启全局事务 流程图地址&#xff1a;https://www.processon.com/view/link/6108de13e0b34d3e35b8e4ef 3.第二阶段全局事务的提交 流程图地址…
阅读更多...
基于深度学习的图像去雨去雾

基于深度学习的图像去雨去雾

基于深度学习的图像去雨去雾 文末附有源码下载地址 b站视频地址&#xff1a; https://www.bilibili.com/video/BV1Jr421p7cT/ 基于深度学习的图像去雨去雾&#xff0c;使用的网络为unet&#xff0c; 网络代码&#xff1a; import torch import torch.nn as nn from torchsumm…
阅读更多...
电脑麦克风没声音怎么设置？一步步教你设置正确！

电脑麦克风没声音怎么设置？一步步教你设置正确！

电脑麦克风是进行语音通话、语音识别和录音等操作时必不可少的设备&#xff0c;然而有时候我们可能会遇到电脑麦克风没有声音的问题&#xff0c;导致无法正常进行语音交流或录音。在本文中&#xff0c;我们将介绍电脑麦克风没声音怎么设置的三种方法&#xff0c;以分步骤详细说…
阅读更多...
AHU 汇编 实验一

AHU 汇编 实验一

一、实验名称&#xff1a;实验1 实验1 用Debug命令查看寄存器和内存中的内容 实验目的:求掌握使用Debug命令查看寄存器和内存的方法。 通过第2章两个简单实例认识汇编语言程序&#xff0c;初步了解程序格式&#xff1b;段定义&#xff1b;标号&#xff1b;DOS系统功能&#xf…
阅读更多...
科技成果鉴定测试如何进行?第三方检测机构进行鉴定测试的好处

科技成果鉴定测试如何进行?第三方检测机构进行鉴定测试的好处

科技成果鉴定测试&#xff0c;作为科技领域中一项重要的质量检验手段&#xff0c;具有广泛的应用范围。旨在为科技成果的研发者和使用者提供客观、科学、权威的鉴定结果&#xff0c;从而评估科技成果的技术水平和市场竞争力。 　　科技成果鉴定测试是对科技成果进行系统、全面的…
阅读更多...
数据结构 day2

数据结构 day2

1:思维导图 2&#xff1a;计算结构体大小 3&#xff1a;大小端存储 &#xff08;1&#xff09;&#xff1a;数据溢出 1 #include <stdio.h>2 #include <string.h>3 #include <stdlib.h>4 int main(int argc, const char *argv[])5 {6 short a 0x1234;…
阅读更多...
自定义方法SQL注入器-DefaultSqlInjector

自定义方法SQL注入器-DefaultSqlInjector

/*** 自定义Sql注入* author zy*/ public class SqlInjector extends DefaultSqlInjector {Overridepublic List<AbstractMethod> getMethodList(Class<?> mapperClass, TableInfo tableInfo) {// 注意&#xff1a;此SQL注入器继承了DefaultSqlInjector(默认注入器…
阅读更多...
性价比高超声波清洗机推荐，热门性价比高超声波清洗机大揭秘!

性价比高超声波清洗机推荐，热门性价比高超声波清洗机大揭秘!

在日常生活中&#xff0c;眼镜不仅是视力矫正的工具&#xff0c;也是提升个人魅力的时尚配饰。然而&#xff0c;长期佩戴眼镜的我们都面临一个共同的难题——眼镜的清洁工作。尘埃、皮肤油脂、甚至是细菌和病毒&#xff0c;都可能附着在眼镜上&#xff0c;不仅影响视觉效果&…
阅读更多...
C++程序设计-第六/七/八章 运算符重载/包含与继承/虚函数和多态性【期末复习|考研复习】

C++程序设计-第六/七/八章 运算符重载/包含与继承/虚函数和多态性【期末复习|考研复习】

前言 总结整理不易&#xff0c;希望大家点赞收藏。 给大家整理了一下C程序设计中的重点概念&#xff0c;以供大家期末复习和考研复习的时候使用。 C程序设计系列文章传送门&#xff1a; 第一章 面向对象基础 第四/五章 函数和类和对象 第六/七/八章 运算符重载/包含与继承/虚函…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023