ElasticSearch学习篇10_Lucene数据存储之BKD动态磁盘树

前言

基础的数据结构如二叉树衍生的的平衡二叉搜索树通过左旋右旋调整树的平衡维护数据，靠着二分算法能满足一维度数据的logN时间复杂度的近似搜索。对于大规模多维度数据近似搜索，Lucene采用一种BKD结构，该结构能很好的空间利用率和性能。
本片博客主要学习常见的多维数据搜索数据结构以及BKD结构搜索过程以及原理。

一、多维数据空间搜索结构

BKD-Tree是基于KD-B-Tree改进而来，而KD-B-Tree又是KD-Tree和B+Tree的结合体，KD-Tree又是我们最熟悉的二叉查找树BST(Binary Search Tree)在多维数据的自然扩展，它是BSP(Binary Space Partitioning)的一种。B+Tree又是对B-Tree的扩展。以下对这几种树的特点简要描述。

KD-Tree

kd是K-Dimensional的所写，k值表示维度，KD-Tree表示能处理K维数据的树结构，当K为1的时候，就转化为了BST结构

维基百科：在计算机科学里，k-d树（k-维树的缩写）是在k维欧几里德空间组织点的数据结构。k-d树可以使用在多种应用场合，如多维键值搜索（例：范围搜寻及最邻近搜索）。k-d树是空间二分算法（binary space partitioning）的一种特殊情况。

首先看BSP，Binary space partitioning(BSP)是一种使用超平面递归划分空间到凸集的一种方法。使用该方法划分空间可以得到表示空间中对象的一个树形数据结构。这个树形数据结构被我们叫做BSP树。

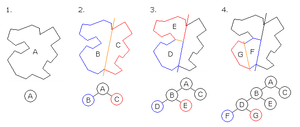
可以分为轴对齐、多边形对齐BSP，这两种方式就是选择超平面的方式不一样，已轴对齐BSP通过构建过程简单理解，就是选择一个超平面，这个超平面是跟选取的轴垂直的一个平面，通过超平面将空间分为两个子空间，然后递归划分子空间。
空间划分思想可以转化为坐标点划分，一般可以应用在游戏中如物体定位等，比如二维空间的四叉树和三维空间的八叉树都是参考BSP划分算法。

BSP树：BSP树使用平面进行递归的二分划分，将空间划分为两个子空间。每个节点要么是叶子节点（包含实际对象），要么是内部节点（包含一个分割平面）。分割平面通常由空间中的一条直线表示。
四叉树：四叉树将空间划分为四个象限，每个象限都是父节点的子节点。每个节点要么是叶子节点（包含实际对象），要么是内部节点（包含四个子节点）。

四叉树又分为点四叉树和边四叉树，以边四叉树为例，具体的实现源码参考：空间搜索优化算法之——四叉树 - 掘金

k-d tree是一种特殊的BSP树，它的特点有：

每一层都是一种划分维度
每个节点代表垂直于当前维度的超平面，将空间划分为两部分
k维空间，按树的每一层循环选取，当前节点为i维，下一层节点为(i+1)%k维

KD 树（KD-tree）和 BSP 树（Binary Space Partitioning tree）都是用于空间划分的数据结构，但它们有一些关键的区别，这也是为什么 KD 树被认为是 BSP 树的一种特殊情况的原因之一。

维度划分方式不同：
- KD 树：KD 树是针对 k 维空间的树形数据结构，它在每个节点上通过轮流选择一个维度来划分空间，例如在二维空间中，它可能在 x 轴上进行一次划分，在 y 轴上进行下一次划分，以此类推。因此，KD 树在每一层都会选择一个维度进行划分。
- BSP 树：BSP 树是一种二叉树，每个节点都代表一个超平面（hyperplane），用于将空间划分为两个子空间。BSP 树的划分方式不一定是轮流选择维度，而是根据一些准则（如最佳平面）选择划分的超平面。
节点类型不同：
- KD 树：KD 树的节点可以是叶节点，也可以是非叶节点。非叶节点表示一个划分超平面，叶节点表示一个数据点。
- BSP 树：BSP 树的每个节点都是一个划分超平面，它没有叶节点来表示数据点。
适用场景不同：
- KD 树：KD 树主要用于 k 维空间中的最近邻搜索等问题，由于它在每个节点上都选择一个维度进行划分，因此在高维空间中可能会出现维度灾难（curse of dimensionality）的问题。
- BSP 树：BSP 树更通用，可以用于任何维度的空间划分，常用于图形学中的空间分区和碰撞检测等问题。

因此，虽然 KD 树和 BSP 树都是空间划分的数据结构，但由于它们的设计和应用场景有所不同，KD 树被认为是 BSP 树的一种特殊情况。

下面是一个2维度的KD-tree，类似BST

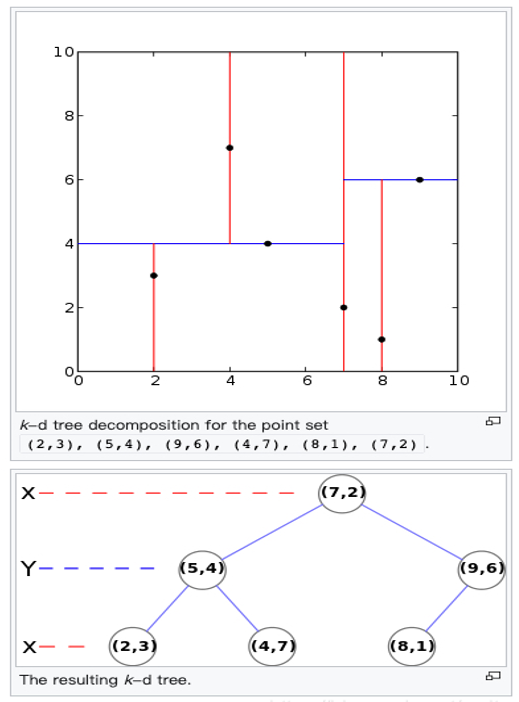
先KD-Tree适宜处理多维数据，查询效率较高。不难知道一个静态多维数据集合建成KD-Tree后查询时间复杂度是O（lgN)。所有节点都存储了数据本身，导致索引数据的内存利用不够紧凑，相应地数据磁盘存储的空间利用不够充分。此外KD-Tree不适宜处理海量数据的动态更新。原因和B树B+树不适宜处理多维数据的动态更新的分析差不多，因为KD-Tree的分层划分是依维度依次轮替进行的，动态更新后调整某个中间节点时，变更的当前维度也同样需要调整其全部子孙节点中的当前维度值，导致对树节点的访问和操作增多，操作耗时增大。可见，KD-Tree更适宜处理的是静态场景的多维海量数据的查询操作。

KD-B-Tree

KD-B-Tree（K-Dimension-Balanced-Tree）顾名思义，结合了KD-Tree和B+Tree。它主要解决了KD-Tree的二叉树形式树高较高，对磁盘IO不够友好的缺点，引入了B+树的多叉树形式，不仅降低了树高，而且全部数据都存储在叶子节点，增加了磁盘空间存储利用率。一个KD-B-Tree结构的示意图如下。它同样不适宜多维数据的动态更新场景，原因同KD-Tree一样。

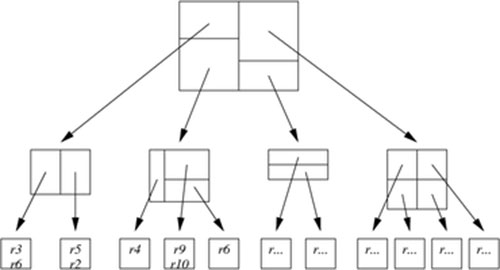
BKD-Tree

BKD-Tree(或BK-D-Tree,全称是Block-K-Dimension-Tree )

二、BKD-Tree原理

在本文中，我们提出了一种新的索引结构，称为Bkd-tree，用于索引大型多维点数据集。 Bkdtree 是一种基于 kd-tree 的 I/O 高效动态数据结构。我们提出了一项广泛的实验研究的结果，表明与之前将 kd-tree 的外部版本动态化的尝试不同，Bkd-tree 保持了其高空间利用率和出色的性能。查询和更新性能与对其执行的更新数量无关。

// TODO