R语言深度学习-3-过拟合问题（无监督正则化/Lasso回归/岭回归/集成和平均算法）

本教程参考《RDeepLearningEssential》

我们从上一个教程看到，我们看到在我们训练迭代或者训练更大神经网络的时候，往往会产生过拟合，而且越来越严重，它可能会把训练它的数据拟合的很好，但是未必能把新数据做的很好。

因此本次介绍一下提升模型泛化能力而防止模型过拟合的方法，称为无监督正则化，通常训练是减少训练误差来优化模型，但是正则化是关注减少测试或训练误差，使得模型在新数据上的效果和训练数据上一样好。

3.1 L1罚函数

3.1.1 Lasso概念

L1罚函数，又称最小绝对值收缩和选择算子（Least Absolute Shrinkage and Selection Operator）是我们熟知的Lasso算法，基本思想是把权重向0收缩，最好淘汰一些不重要的系数，比如一个八元一次方程，描述多种生活习惯对寿命的影响，其中有一个每天刷牙应该属于被去掉的项。

除了防止过拟合之外，它还可以作为一种变量选择的方法。惩罚的力度是由一个超参数λ所控制的，它乘以权重绝对值的和，可以被预先设定，或者就像其他超参数那样，使用交叉验证或者一些类似的方法来优化。

首先，很明显惩罚的影响依赖于权重的大小，而权重的大小依赖于数据的规模。因此，我们通常先把数据标准化为带有单位方差(或者起码是每个变量的方差相等)的形式。

我们用 X 表示输入，Y 表示输出或者因变量，B 是参数，F 是为了求出 B 而要优化的目标函数。特别地有:F(B;X,Y)。在神经网络中，参数可以是偏差或者偏移(本质上是来自回归的截距)以及权重。L1 罚函数把目标函数修正为其中 w 仅代表权重(就是说，偏移通常是被忽略的)。考虑梯度，我们可以将这个增加的惩罚项表示为

$F(B;X,Y)+\lambda ||\omega ||1$

3.1.2 Lasso代码示例

我们通过一个模拟线性回归问题来看一下L1罚函数的工作原理：

我们创建一个具有特定均值和相关性的多元正态分布数据集X，然后根据这些数据和给定的线性模型参数生成了一个响应变量y。

library("glmnet")
library("MASS")
set.seed(1234)
X <- mvrnorm(n = 200, mu = c(0, 0, 0, 0, 0),Sigma = matrix(c(1, .9999, .99, .99, .10,.9999, 1, .99, .99, .10,.99, .99, 1, .99, .10,.99, .99, .99, 1, .10,.10, .10, .10, .10, 1), ncol = 5))
y <- rnorm(200, 3 + X %*% matrix(c(1, 1, 1, 1, 0)), .5)

我们通过glmnet包来拟合L1罚函数，其中是L1还是L2由alpha决定，当alpha取1，是Lasso（L1），当alpha取2，则是岭回归（L2）。而且，当我们并不知道应该选取的 lambda 的值，我们能评价一系列的选择并且使用交叉验证自动调出这个超参数，这可以用 cv.glmnet() 函数来实现。

m.ols <- lm(y[1:100] ~ X[1:100, ])
m.lasso.cv <- cv.glmnet(X[1:100, ], y[1:100], alpha = 1)
plot(m.lasso.cv)

我们发现lasso在比较小的λ值情况下，有比较好的效果，但是随着λ增大，交叉验证模型的误差增大，所以lasso究竟是不是一个很好的算法呢，有待讨论。

cbind(OLS = coef(m.ols),Lasso = coef(m.lasso.cv)[,1])

通过比较拉索得到的系数和线性回归得到的系数，我们发现最后一个系数收缩为0了。

3.2 L2罚函数

3.2.1岭回归概念

L2罚函数，又称岭回归（ridge regression），许多方面和L1罚函数相似，不过他是基于权重平方和而不是基于权重绝对值的和，因此更大的（正或负）权重导致了更大的惩罚。在神经网络背景下，也称作权重衰减，他的公式是

$F(B;X,Y)+\lambda ||\omega ||2$

L1和L2两者之间的主要区别在于：
（1）稀疏性：L1正则化倾向于产生稀疏解，即许多参数最终变为零，而L2正则化不会产生这样的效果。
（2）连续性和平滑性：L2正则化保持了权重的连续性，使得学习到的权重更容易解释；而L1正则化可能导致不连续的权重，使得模型的解释性变差。
（3）抗噪声能力：L2正则化对于噪声更鲁棒，因为它对每个参数施加了相同的惩罚，而L1正则化可能对一些异常值敏感。
（4）计算复杂性：L1正则化通常比L2正则化计算起来更复杂，因为L1正则化涉及到绝对值的计算，这在数值优化中可能导致一些问题。
在实际应用中，选择哪种正则化方法取决于具体问题和数据的特性。例如，当特征数量远大于样本数量时，L1正则化可以帮助进行特征选择；而在特征数量与样本数量相近的情况下，L2正则化可能更适合。

3.2.2岭回归代码示例

m.ridge.cv <- cv.glmnet(X[1:100, ], y[1:100], alpha = 0)
plot(m.ridge.cv)
cbind(OLS = coef(m.ols),Lasso = coef(m.lasso.cv)[,1],Ridge = coef(m.ridge.cv)[,1])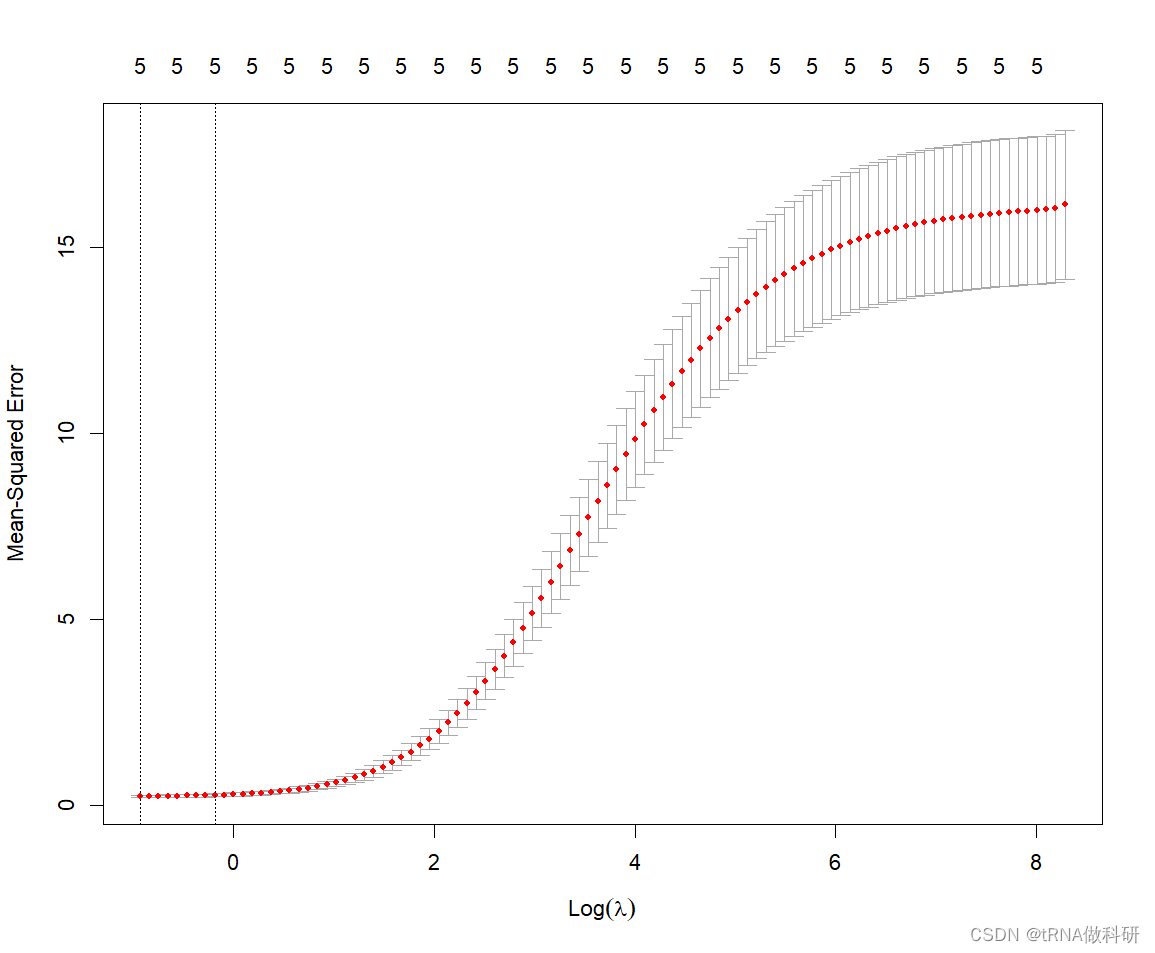

尽管Ridge并没有把系数收缩到0，但是比起单纯的线性回归，也降低了重要的参数

3.3权重衰减-神经网络使用L2罚函数

我们在上一篇中已经小试牛刀，使用caret包和nnet包训练的神经网络使用了0.01的权重衰减，我们现在通过交叉验证的方式来进一步探究权重衰减对神经网络的影响。数据请看上一篇：

R语言深度学习-2-训练预测模型-CSDN博客

dig_train <- read.csv("C:\\Users\\Huzhuocheng\\Desktop\\digit-recognizer\\train.csv")
dim(dig_train) #数据维度查看
dig_train$label <- factor(dig_train$label, levels = 0:9)
i <- 1:6000
dig_X <- dig_train[i, -1]
dig_Y <- dig_train[i, 1]
#比较不同的权重衰减
set.seed(1234)
dig_m1 <- lapply(c(100,150), function(its) {train(dig_X, dig_Y,method = 'nnet',tuneGrid = expand.grid(.size = c(10),.decay = c(0, .1)),trControl = trainControl(method = 'cv', number = 5,repeats = 1),MaxNWts = 10000,maxit = its)
})

我们发现正则化的准确度并没有非正则化的表现好，这是在100次迭代的情况下，那我们再看一下更多次的迭代后的情况：

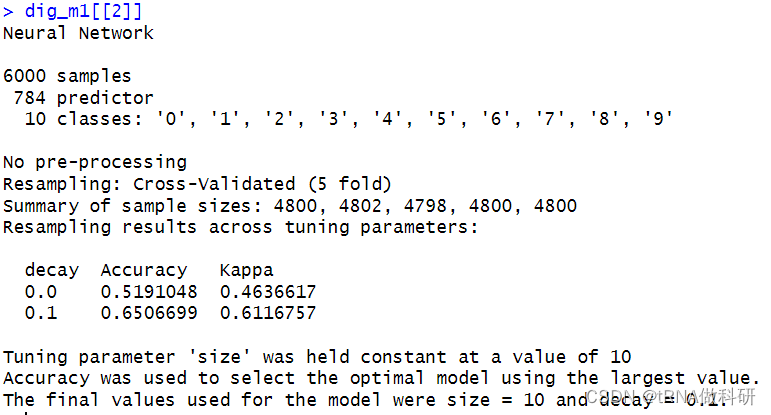
这时我们发现，在比较高的迭代次数下，我们正则化的表现比非正则化的要好很多，所以正则化在相对更复杂，更大的拟合模型中有较好的表现。

3.4集成和模型平均

这个的想法是我们实现一次拟合会采用不同的算法，那么有的算法可能会过高，有的算法可能会过低，那我们将个别算法的结果组合起来，可以相互抵消。我们举个例子：

set.seed(1234)
d <- data.frame(x = rnorm(400))
d$y <- with(d, rnorm(400, 2 + ifelse(x < 0, x + x^2, x + x^2.5),1))
d.train <- d[1:200, ]
d.test <- d[201:400, ]
## three different models
m1 <- lm(y ~ x, data = d.train)
m2 <- lm(y ~ I(x^2), data = d.train)
m3 <- lm(y ~ pmax(x, 0) + pmin(x, 0), data = d.train)
cbind(M1 = summary(m1)$r.squared,M2 = summary(m2)$r.squared,M3 = summary(m3)$r.squared)

我们构建一个满足正态分布的分段函数，然后分别用简单线性回归（m1），非线性回归（m2），分段函数回归（m3）进行拟合，然后我们看三种建模的拟合效果：是相差很大的

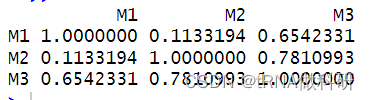
我们再看一下每种模型的拟合相关性，可以得到模型预测间有多大重叠。

cor(cbind(M1 = fitted(m1),M2 = fitted(m2),M3 = fitted(m3)
))

我们进行我们的思路，集成和模型平均：

d.test$yhat1 <- predict(m1, newdata = d.test)
d.test$yhat2 <- predict(m2, newdata = d.test)
d.test$yhat3 <- predict(m3, newdata = d.test)
d.test$yhatavg <- rowMeans(d.test[, paste0("yhat", 1:3)])cor(d.test)

我们发现得到的y预测中，模型平均得到的预测优于三种中任何一种：