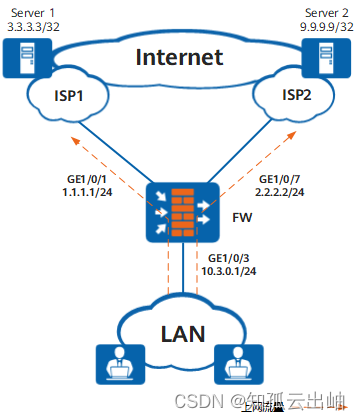
审题
第三问要我们评估七鳃鳗的性别比例变化对生态系统稳定性的影响。
这里我们就要去查一下生态系统稳定性的定义。
通过查资料我们知道,生态系统稳定性包括生态系统的抵抗力和恢复力。
OK,到这里问题就变成了,七鳃鳗的性别比例对生态系统的抵抗力和恢复力的影响。
那怎么去评估,生态系统的抵抗力和恢复力就是接下来的问题。
通过查资料我们发现,评估生态系统的抵抗力和恢复力是没有一个统一的方法的。这就需要我们具体问题具体分析,但是我们也可以别人是怎么去评估生态系统的抵抗力和恢复力的。
这里评估台风对生态系统的抵抗力和恢复力的文章:


它这里提出的方法就是计算台风出现前后,植被的面积的变化率作为评价生态系统抵抗力的指标。
回复力同理,也是计算植被面积的分辨率作为评价生态系统的恢复力。
抓住重点,就是种群数量前后的变化率,是评价生态系统稳定性的关键。
借鉴上面的方法,我们提出了我们这道题的生态系统稳定性评价方法。
生态系统抵抗力
这里我们假设,生态系统中原本生存了700条湖鳟,生态系统稳定。这时生态系统中有100条七鳃鳗入侵,对生态系统造成了破坏,湖鳟数量开始下降。好了,这时我们就看七鳃鳗入侵一定时间后,比如700天,湖鳟鱼的数量下降了多少。通过计算入侵前后的湖鳟数量变化率来评价生态系统的抵抗力。
注意,我们这里可以让100条七鳃鳗以不同性别比例入侵这个生态系统,这样湖鳟鱼的最后的变化率也是不同的。以此我们来评价不同性别比例对生态系统抵抗力的影响。
这里计算湖鳟鱼的种群数量用到第一问的公式,变化率用如下公式:

变化率 = (初始种群数 - 一段时间后的种群数)/ 初始种群数
生态系统恢复力
恢复力同理,700天后让100条七鳃鳗移除生态系统,这时湖鳟种群数量已经低于初始值。我们再计算多少天的时间,湖鳟鱼的数量可以恢复到初始值,以此评价生态系统的恢复力。
同理,我们也是让100条七鳃鳗以不同性别比例入侵这个生态系统,让后再以此,这时生态系统的恢复力也是不同的。以此我们来评价不同性别比例对生态系统恢复力的影响。

公式如上, 恢复率 = (初始种群数 - 一段时间后的种群数)/ 恢复天数
计算结果
性别比例对抵抗力的影响
湖鳟鱼为700,七鳃鳗为100,在性别比例不同下,湖鳟鱼的变化曲线。

去掉七鳃鳗后湖鳟鱼的数量

计算抵抗力,并作性别比例和变化率的关系图。

可以看到,雄性占比为0.5时,湖鳟鱼的变化率更大,意味着对生态系统的破坏更大,导致生态系统抵抗力下降。随着雄鱼占比增加,湖鳟鱼的变化率减小,意味着对生态系统破坏小。
性别比例对恢复力的影响
700天后,将七鳃鳗去除,湖鳟鱼在去除后的数量进行增长,看多少天能恢复到初始值。

同样,做性别比例和恢复率的关系图
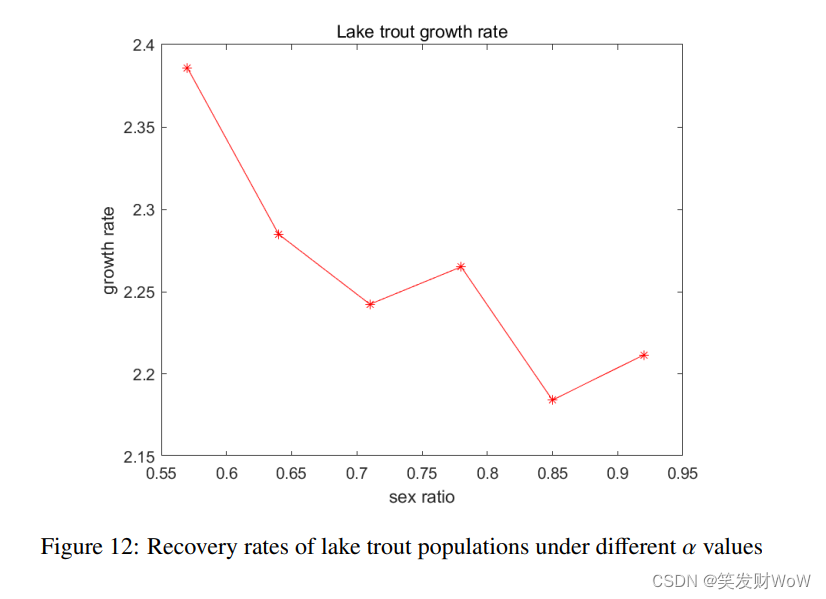
同样,可以看到雄性占比在0.5时,恢复速度较快,意味着恢复力较强。随着雄性占比减少,恢复速度降低,恢复力减弱。
代码
% 参数定义
r = 0.03; % 增长率
K = 700; % 环境承载能力
N0 = K; % 初始种群数量
d = 0.01;%死亡率
alpha = 0.5;
alpha_lis = [alpha];
N_l = 100;%七鳃鳗数量
a = 0.023*alpha*N_l + 0.029 * (1-alpha) * N_l;%捕食量
w = 4;
W = a/w;
% 时间跨度
tspan = [0, 700]; % 从0到100个时间单位% 定义微分方程
%odefun = @(t, N) r*N(1) * (1 - N(1)/K) - a - d*N;for i=1:6% 定义微分方程odefun = @(t, N) r*N(1) * (1 - N(1)/K) - a - d*N;% 使用ode45求解微分方程[t, N(:,i)] = ode45(odefun, tspan, N0);alpha = alpha + 0.07;alpha_lis = [alpha_lis,alpha];a = 0.023*alpha*N_l + 0.029 * (1-alpha) * N_l;W = a/w;
end
% 绘制结果
figure
plot(t, N);
xlabel('Time');
ylabel('Population N');
title('Population Dynamics');
%text('K=1000','FontSize','right');% 在曲线末尾的x值处添加文本
text(t(end), N(end,1), ['N= ', num2str(N(end,1)),' ','K=',num2str(K)], 'HorizontalAlignment', 'right');yline(0,'r')
% 设置图例位置
legend(['alpha = ',num2str(alpha_lis(1))], ...['alpha = ',num2str(alpha_lis(2))], ...['alpha = ',num2str(alpha_lis(3))], ...['alpha = ',num2str(alpha_lis(4))], ...['alpha = ',num2str(alpha_lis(5))], ...['alpha = ',num2str(alpha_lis(6))]);
%grid on;figure
plot(alpha_lis(:,1:6),(700-N(end,:))/700,'r-*');
title('The rate of loss of the sex ratio to the ecosystem')
ylabel('loss rate')
xlabel('sex ratio')n = N(end,:);
N = [];
alpha = 0.5;
alpha_lis = [];
figure
for i =1:6% 定义微分方程odefun = @(t, N) r*N(1) * (1 - N(1)/K) ;% 使用ode45求解微分方程[t, N] = ode45(odefun, tspan, n(i));subplot(2,3,i);plot(t, N, 'g', 'LineWidth', 2,'Color','r'); % 种群总数N(t)xlabel('Time');ylabel('Population (N)');title(['alpha=',num2str(alpha)]);yline(200,'b','LineWidth',2)alpha = alpha + 0.07;alpha_lis = [alpha_lis,alpha];
end