leetcode 3.11

leetcode hot 100

- 二分查找
- - 1.寻找旋转排序数组中的最小值
- 矩阵
- - 1.搜索二维矩阵 II
  - - 知识点：upper_bound, lower_bound
    - 知识点：二分查找
  - 2.搜索二维矩阵
- 链表
- - 1.合并两个有序链表
  - 2.两数相加
  - 3. 删除链表的倒数第 N 个结点

二分查找

1.寻找旋转排序数组中的最小值

寻找旋转排序数组中的最小值
根据题意可知，一定存在一个点，让整个数组断崖式下跌，
[7, 6, 5, 4, 3, 2, 0, 1] 比如在这个数组中的0
我们需要找到这个断崖式下跌的点，就是这个数组的最小值
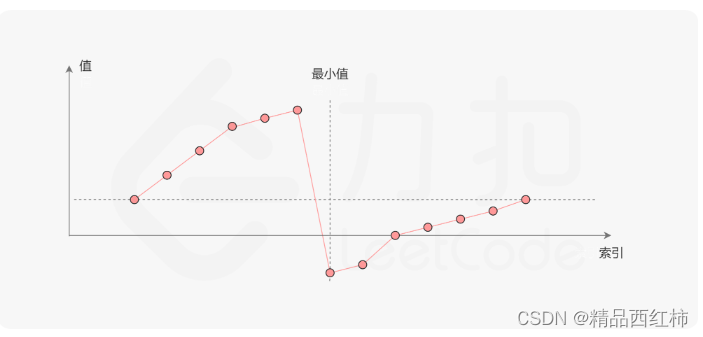
在这里插入图片描述
我们考虑数组中的最后一个元素 x：在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 x；而在最小值左侧的元素，它们的值一定都严格大于 x。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。
查找第一个大于等于目标值的元素（加了其它代码的解释，原来的题解放在链接里了）

class Solution {
public:int findMin(vector<int>& nums) {int low  = 0; int high = nums.size() - 1;while (low  < high) {int pivot = low + (high - low) / 2;if (nums[pivot] < nums[high]) {high = pivot;} else {low  = pivot + 1;}}return nums[low];}
};

矩阵

1.搜索二维矩阵 II

240. 搜索二维矩阵 II

第一种：最容易想到的暴力解法
时间复杂度：o(mn)
空间复杂度：o(1)

第二种：暴力解法的进阶版，用二分查找每一行，这样可以减少时间复杂度
时间复杂度：o(nlogn)
空间复杂度：o(1)

第三种：比较巧妙的方法，从左上或者右下角开始查找，以右下角matrix[n - 1][0] 为例，如果当前matrix[i][j] 值为 a

如果我们找的元素target大于a，那么 j++ 寻找
如果我们找的元素target小于a，那么 i-- 寻找
如果等于，则直接返回

第二种: 二分优化暴力查找

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();for (int i = 0; i < n; i++) {auto ans = lower_bound(matrix[i].begin(), matrix[i].end(), target);//auto tmp = ans - matrix[i].begin();//if (ans != matrix[i].end() &&  matrix[i][tmp] == target) {if (ans != matrix[i].end() && *ans == target) {return true;}}return false;}
};

或者不用库函数，手写二分：

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();for (int i = 0; i < n; i++) {int l = 0, r = m;while (l < r) {int mid = (r - l) / 2 + l;if (matrix[i][mid] < target) {l = mid + 1;} else {r = mid;}}if (l < m && matrix[i][l] == target) return true;}return false;}
};

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();for (int i = 0; i < n; i++) {int l = 0, r = m - 1;while (l <= r) {int mid = (r - l) / 2 + l;if (matrix[i][mid] < target) {l = mid + 1;} else  if (matrix[i][mid] > target) {r = mid - 1;} else {return true;}}}return false;}
};

知识点：upper_bound, lower_bound

upper_bound, lower_bound两者都是定义在头文件里。用二分查找的方法在一个排好序的数组中进行查找。既然是二分，时间复杂度就是O(logN)。

基础用法

upper_bound(begin, end, value)

在从小到大的排好序的数组中，在数组的 [begin, end) 区间中二分查找第一个大于value的数，找到返回该数字的地址，没找到则返回end。

lower_bound(begin, end, value)

在从小到大的排好序的数组中，在数组的 [begin, end) 区间中二分查找第一个大于等于value的数，找到返回该数字的地址，没找到则返回end。

用greater()重载

upper_bound(begin, end, value, greater<int>())

在从大到小的排好序的数组中，在数组的 [begin, end) 区间中二分查找第一个小于value的数，找到返回该数字的地址，没找到则返回end。

lower_bound(begin, end, value, greater<int>())

在从大到小的排好序的数组中，在数组的 [begin, end) 区间中二分查找第一个小于等于value的数，找到返回该数字的地址，没找到则返回end。

第三种：将二维矩阵抽象成「以右上角为根的 BST」

以右上为根

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();int i = 0, j = m - 1;while (i < n && j >= 0) {if (matrix[i][j] > target) j--;else if (matrix[i][j] < target) i++;else return true;}return false;}
};

以左下为根……

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();int i = n - 1, j = 0;while (i >= 0 && j < m) {if (matrix[i][j] > target) i--;else if (matrix[i][j] < target) j++;else return true;}return false;}
};

知识点：二分查找

二分查找的难点在于边界判断，如果实在没法判断可以写几个数字自己模拟二分过程推导一次就能得出结论。以下为个人总结，仅供参考

记住两个模板，在这两个模板上修改：
当我们需要查找第一个大于等于target的数时：

第一种方法：
- r = n
- l < r不加等号，这样l == r 时会返回
- 需要判断 >= target 的情况，因为如果用<=会导致死循环
- return l/ r

int l = 0, r = n;
while (l < r) {......if (nums[mid] >= targer) {r = mid;} else {l = mid + 1;}
}

第二种方法：
- r = n - 1
- l <= r 加等号，这样l > r (l > r && r - l = 1) 时会返回
- 加上 == target 的情况判断会比较清晰（个人习惯）
- return l (也就是r + 1)

int l = 0, r = n - 1;
while (l <= r) {......if (nums[mid] == target) {return mid + 1;} else if (nums[mid] < target) {l = mid + 1;} else {r = mid - 1;}
}
return l;

当我们需要查找第一个大于target的数时：

第一种方法：
- r = n
- l < r不加等号，这样l == r 时会返回
- 需要判断 >= target 的情况，因为如果用<=会导致死循环
- 判断结果，如果等于则return l + 1, 否则return l (也就是r + 1)

int l = 0, r = n;
while (l < r) {......if (nums[mid] >= targer) {r = mid;} else {l = mid + 1;}
}

第二种方法：
- r = n - 1
- l <= r 加等号，这样l > r (l > r && r - l = 1) 时会返回
- 加上 == target 的情况判断会比较清晰（个人习惯）
- 判断结果，如果等于则return mid + 1, 否则return l (也就是r + 1)

int l = 0, r = n - 1;
while (l <= r) {......if (nums[mid] == target) {return mid + 1;} else if (nums[mid] < target) {l = mid + 1;} else {r = mid - 1;}
}
return l;

同理可以推出其他情况。

现在让我们用抽象成BST的方法来重新做以下这道题

2.搜索二维矩阵

搜索二维矩阵
我们从以右上为根节点

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {vector<int> ans;int n = matrix.size(), m = matrix[0].size();int i = 0, j = m - 1;while (i < n && j >= 0) {if (matrix[i][j] > target) {j--;} else if (matrix[i][j] < target) {i++;} else return true;}return false;}
};

链表

1.合并两个有序链表

合并两个有序链表
方法一：迭代
当 list1 和 list2都不为空时，依次连接，之后判断哪个链表不为空，把剩余链表合并。
时间复杂度：O(n+m)
空间复杂度：O(1)

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {ListNode* dummy = new ListNode(-1);ListNode* ans = dummy;while (list1 != nullptr && list2 != nullptr) {if (list1->val < list2->val) {ans->next = list1;list1 = list1->next;} else {ans->next = list2;list2 = list2->next;}ans = ans->next;}ans->next = list1 == nullptr ? list2 : list1;return dummy->next;}
};

方法二：递归

一开始并没有想到这个递归方法，所以需要再次复习递归的知识点：

递归函数必须要有终止条件，否则会出错；
递归函数先不断调用自身，直到遇到终止条件后进行回溯，最终返回答案。

在此题中，终止条件就是list1 == nullptr || list2 == nullptr
我们可以如下递归地定义两个链表里的 merge 操作（忽略边界情况，比如空链表等）：

list1[0] + merge(list1[1:], list2) list1[0] < list2[0]
list2[0] + merge(list1, list2[1:]) otherwise

也就是说，两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if (list1 == nullptr) return list2;else if (list2 == nullptr) return list1;else if (list1->val < list2->val) {list1->next = mergeTwoLists(list1->next, list2);return list1;} else {list2->next = mergeTwoLists(list1, list2->next);return list2;}}
};

2.两数相加

两数相加
暴力思路：先把链表转为int, 加起来之后再放到int里，那肯定是会超时/超空间的
看了题解可以发现：
1.如果遍历到某个链表之后为空，值为0
2.链表每一位上的和为（list1->val + list2->val + carry）% 10，carry为上一位的进位，初始值为0
3.链表每一位上的进位为 carry = (list1->val + list2->val + carry) / 10
4.因为是逆序存储，那么直接计算，如果最后一位有进位，那么end->next后再new 一个 node(1)

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode* dummy = new ListNode(-1);ListNode* result = dummy;int carry = 0;while (l1 != nullptr || l2 != nullptr) {int x = l1 == nullptr ? 0 : l1->val;int y = l2 == nullptr ? 0 : l2->val;int tmp = (x + y + carry) % 10;result->next = new ListNode(tmp);result = result->next;carry = (x + y + carry) / 10;if (l1 != nullptr) l1 = l1->next;if (l2 != nullptr) l2 = l2->next;}if (carry) result->next = new ListNode(1);return dummy->next;}
};

3. 删除链表的倒数第 N 个结点

删除链表的倒数第 N 个结点
第一次遍历得出链表个数，第二次遍历删除节点

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {ListNode* p = head, *q = head;int num = 0;while(p != nullptr) {p = p->next;num++;}// 如果要删除的节点是第一个节点，直接返回第二个节点即可if (num == n) return head->next;num = num - n - 1;while (num--) {q = q->next;}//如果要删除的是最后一个节点之后的节点，空节点，直接return headif (q->next != nullptr)q->next = q->next->next;return head;}
};