一 深度学习基础相关
深度学习三个主要的方向:计算机视觉,自然语言,语音识别。
机器学习核心组件:1 数据集(data),2 前向传播的model(net),3 目标函数(loss), 4 调整模型参数和优化函数的算法(adam)。
数据集:用于模型训练的数据。
模型:用于前向传播计算的model, 其中涉及各种复杂的网络,Alexnet, CNN等都属于这个模块的内容,对于传统模型,常规使用公式计算结果的公式其实就是模型的一种,模型主要作用是通过记录的参数计算想要的目标值。
目标函数:常用的均方误差,平方误差都是,目标函数的一直,用于评估预测值和实际结果的偏差。
优化算法:深度学习常用的梯度下降算法,在训练模型参数时用于减小损失误差。
不管是回归还是分类问题其实都是监督学习的内容,就是在训练模型是有一个目标值,而聚类算法,对抗性网络等属于无监督学习。
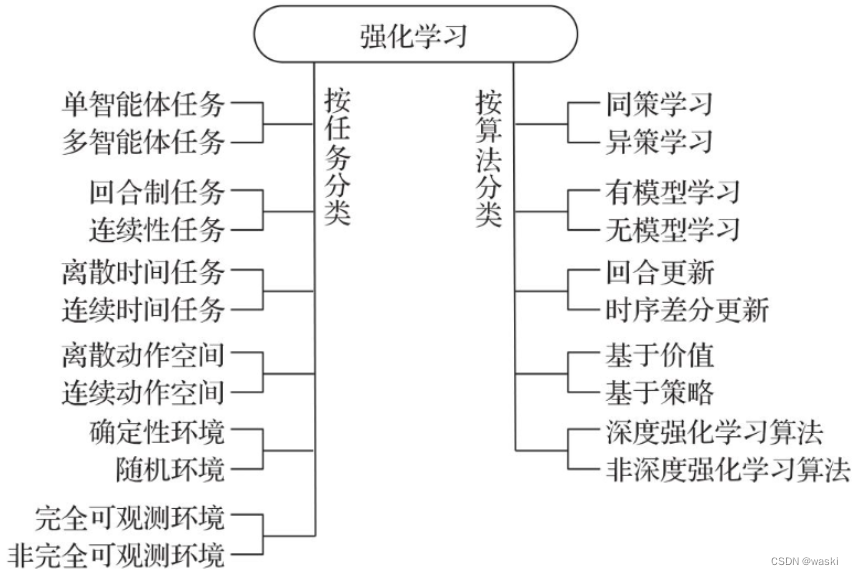
强化学习更考虑与环境的互动,在实际环境中根据实际结果做反馈实时修正模型。
PS:机器学习很吃数据,如果数据量不够,可能得考虑传统方法,比如之前遇到的一个项目,训练数据不够,属于前期就介入,根本没太多历史数据,不能够拟合出正确应对实际场景的应用,最后使用传统反馈调整的模式解决了问题,做视觉其实也遇到了这个问题,异常数据太少,而且不是很普遍,还是考虑传统方式处理,起码稳定。
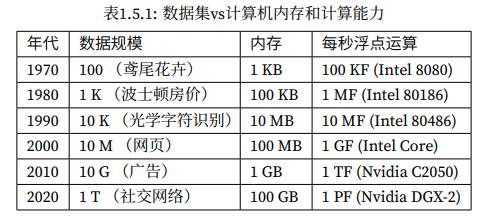
计算机算力确实发生了很大的变化,近两年还是风云突变:
二 pytorch 基础操作
2.1 数据生成 (pytorch叫张量)
import torch
import torchvisionx = torch.arange(12)
x # tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])查看数据形状:
x.shape# torch.Size([12])查看张量的总数据量:
x.numel() # 矩阵元素数量 # 12调整张量的形状:
X = x.reshape(3, 4)
X
# tensor([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]])生成指定形状的数组:
torch.zeros((2, 3, 4))
# tensor([[[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]],# [[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]]])指定形状数据为1的张量:
torch.ones((2, 3, 4))
# tensor([[[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]],# [[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]]])正太分布的张量:
torch.randn(3, 4)
# tensor([[ 1.2365, 0.2051, 1.0180, 1.2629],
# [-1.2494, -0.3436, -0.7135, -2.0160],
# [-1.2806, 1.5036, -0.2523, -0.1456]])直接将列表转换为tensor张量:
torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
# tensor([[2, 1, 4, 3],
# [1, 2, 3, 4],
# [4, 3, 2, 1]])2.2 pytorch 运算符
可以直接 + - * /:
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y # **运算符是求幂运算
# (tensor([ 3., 4., 6., 10.]),
# tensor([-1., 0., 2., 6.]),
# tensor([ 2., 4., 8., 16.]),
# tensor([0.5000, 1.0000, 2.0000, 4.0000]),
# tensor([ 1., 4., 16., 64.]))求幂:
torch.exp(x) # e^x
# tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])张量拼接,通过dim指定行还是列拼接:
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
# (tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [ 2., 1., 4., 3.],
# [ 1., 2., 3., 4.],
# [ 4., 3., 2., 1.]]),
# tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
# [ 4., 5., 6., 7., 1., 2., 3., 4.],
# [ 8., 9., 10., 11., 4., 3., 2., 1.]]))逻辑运算:
X == Y
# tensor([[False, True, False, True],
# [False, False, False, False],
# [False, False, False, False]])所有元素求和:
X.sum()
# tensor(66.)2.3 广播机制
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b
# (tensor([[0],
# [1],
# [2]]),
# tensor([[0, 1]]))自动广播:
a + b
# tensor([[0, 1],
# [1, 2],
# [2, 3]])2.4 索引和切片
张量切片:
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
X[-1], X[1:3]
# (tensor([ 8., 9., 10., 11.]),
# tensor([[ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]]))指定位置写入数据:
X[1, 2] = 9
X
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 9., 7.],
# [ 8., 9., 10., 11.]])同时写入多个值:
X[0:2, :] = 12
X
# tensor([[12., 12., 12., 12.],
# [12., 12., 12., 12.],
# [ 8., 9., 10., 11.]])2.5 原地更新参数
查看内存地址:
before = id(Y)
Y = Y + X
id(Y) == before
# False张量原地更新:
Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))
# id(Z): 2385633027792
# id(Z): 2385633027792也可以直接写入原地址:
before = id(X)
X += Y
id(X) == before
# True2.6 转换为python其他数据类型
numpy转换, torch.tensor() :
A = X.numpy()
B = torch.tensor(A)
type(A), type(B)
# (numpy.ndarray, torch.Tensor)直接转换,a.item() 用于获取张量(Tensor)中单个元素 的值:
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
# (tensor([3.5000]), 3.5, 3.5, 3)三 数据预处理
3.1 读取数据集
创建数据写入 house_tiny.csv 文件:
import os
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:f.write('NumRooms,Alley,Price\n') # 列名f.write('NA,Pave,127500\n') # 每行表示一个数据样本f.write('2,NA,106000\n')f.write('4,NA,178100\n')f.write('NA,NA,140000\n')pd.read_csv() 读取数据:
import pandas as pd
data = pd.read_csv(data_file)
print(data)
# NumRooms Alley Price
# 0 NaN Pave 127500
# 1 2.0 NaN 106000
# 2 4.0 NaN 178100
# 3 NaN NaN 1400003.2 处理缺失值
第一列均值填充:
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
# 使用均值填充第一列的缺失值
inputs.iloc[:, 0] = inputs.iloc[:, 0].fillna(inputs.iloc[:, 0].mean())
print(inputs)
# NumRooms Alley
# 0 3.0 Pave
# 1 2.0 NaN
# 2 4.0 NaN
# 3 3.0 NaN第二列独热编码:
inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)
# NumRooms Alley_Pave Alley_nan
# 0 3.0 True False
# 1 2.0 False True
# 2 4.0 False True
# 3 3.0 False True数据格式转换为张量:
import torch
X = torch.tensor(inputs.to_numpy(dtype=float))
y = torch.tensor(outputs.to_numpy(dtype=float))
X, y
# (tensor([[3., 1., 0.],
# [2., 0., 1.],
# [4., 0., 1.],
# [3., 0., 1.]], dtype=torch.float64),
# tensor([127500., 106000., 178100., 140000.], dtype=torch.float64))四 线性代数
标量:
import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x**y
# (tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))向量可以被视为标量值组成的列表:
x = torch.arange(4)
x
# tensor([0, 1, 2, 3])下标 取元素:
x[3]
# tensor(3)向量 长度:
len(x)
# 4张量形状:
x.shape
# torch.Size([4])4.1 矩阵
向量将标量从零阶推广到一阶,矩阵将向量从一阶推广到二阶。
A = torch.arange(20).reshape(5, 4)
A
# tensor([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11],
# [12, 13, 14, 15],
# [16, 17, 18, 19]])矩阵转置:
A.T
# tensor([[ 0, 4, 8, 12, 16],
# [ 1, 5, 9, 13, 17],
# [ 2, 6, 10, 14, 18],
# [ 3, 7, 11, 15, 19]])对称矩阵,一个矩阵和它的转置矩阵一样的时候该矩阵为对称矩阵:
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
# tensor([[1, 2, 3],
# [2, 0, 4],
# [3, 4, 5]])B == B.T
# tensor([[True, True, True],
# [True, True, True],
# [True, True, True]])4.2 张量
张量是一个更广泛的概念,可以包括标量、向量以及更高维度的数组。
X = torch.arange(24).reshape(2, 3, 4)
X
# tensor([[[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]],# [[12, 13, 14, 15],
# [16, 17, 18, 19],
# [20, 21, 22, 23]]])4.3 张量算法的基本性质
给定具有相同形 状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。例如,将两个相同形状的矩阵相加, 会在这两个矩阵上执行元素加法,张量形状不变。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
A, A + B
# (tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [12., 13., 14., 15.],
# [16., 17., 18., 19.]]),
# tensor([[ 0., 2., 4., 6.],
# [ 8., 10., 12., 14.],
# [16., 18., 20., 22.],
# [24., 26., 28., 30.],
# [32., 34., 36., 38.]]))A * B
# tensor([[ 0., 1., 4., 9.],
# [ 16., 25., 36., 49.],
# [ 64., 81., 100., 121.],
# [144., 169., 196., 225.],
# [256., 289., 324., 361.]])将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘,广播机制。
a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape
# (tensor([[[ 2, 3, 4, 5],
# [ 6, 7, 8, 9],
# [10, 11, 12, 13]],# [[14, 15, 16, 17],
# [18, 19, 20, 21],
# [22, 23, 24, 25]]]),
# torch.Size([2, 3, 4]))4.4 降维
x = torch.arange(4, dtype=torch.float32)
x, x.sum()
# (tensor([0., 1., 2., 3.]), tensor(6.))sum() 可以对所有元素求和,算预测结果损失和有用:
A.shape, A.sum()
# (torch.Size([5, 4]), tensor(190.))axis 指定张量降维维度:
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
# (tensor([40., 45., 50., 55.]), torch.Size([4]))A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
# (tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))A.sum(axis=[0, 1]) # 结果和A.sum()相同
# tensor(190.)求所有元素均值:
A.mean(), A.sum() / A.numel()
# (tensor(9.5000), tensor(9.5000))指定维度均值:
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
# (tensor([ 8., 9., 10., 11.]), tensor([ 8., 9., 10., 11.]))非降维求和:
sum_A = A.sum(axis=1, keepdims=True)
sum_A
# # tensor([[ 6.],
# [22.],
# [38.],
# [54.],
# [70.]])由于sum_A在对每行进行求和后仍保持两个轴,我们可以通过广播将A除以sum_A,求该行每个元素的占比。
A / sum_A
# tensor([[0.0000, 0.1667, 0.3333, 0.5000],
# [0.1818, 0.2273, 0.2727, 0.3182],
# [0.2105, 0.2368, 0.2632, 0.2895],
# [0.2222, 0.2407, 0.2593, 0.2778],
# [0.2286, 0.2429, 0.2571, 0.2714]])沿某个轴计算A元素的累积总和,比如axis=0(按行计算),可以调用cumsum函数。
print(A)
A.cumsum(axis=0)
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [12., 13., 14., 15.],
# [16., 17., 18., 19.]])
# tensor([[ 0., 1., 2., 3.],
# [ 4., 6., 8., 10.],
# [12., 15., 18., 21.],
# [24., 28., 32., 36.],
# [40., 45., 50., 55.]])4.5 点积
深度学习中线性模型在 前向传播中使用的就是点积:
x = torch.arange(4, dtype=torch.float32)
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)
# (tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))可以通过执行按元素乘法,然后进行求和来表示两个向量的点积:
torch.sum(x * y)
# tensor(6.)矩阵向量积,结果是一个新的向量,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同:
print(A)
print(x)
A.shape, x.shape, torch.mv(A, x)
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [12., 13., 14., 15.],
# [16., 17., 18., 19.]])
# tensor([0., 1., 2., 3.])
# (torch.Size([5, 4]), torch.Size([4]), tensor([ 14., 38., 62., 86., 110.]))矩阵-矩阵乘法,torch.mm 用于计算两个矩阵的乘积:
B = torch.ones(4, 3)
A, B, torch.mm(A, B)
# (tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [12., 13., 14., 15.],
# [16., 17., 18., 19.]]),
# tensor([[1., 1., 1.],
# [1., 1., 1.],
# [1., 1., 1.],
# [1., 1., 1.]]),
# tensor([[ 6., 6., 6.],
# [22., 22., 22.],
# [38., 38., 38.],
# [54., 54., 54.],
# [70., 70., 70.]]))4.6 范数
欧几里得距离是一个L2范数,向量元素平方和的平方根:

u = torch.tensor([3.0, -4.0])
torch.norm(u)
# tensor(5.)L1范数,我们将元素绝对值求和 组合起来:
torch.abs(u).sum()
# tensor(7.)Frobenius范数 满足向量范数的所有性质,它就像是 矩阵形向量的L2范数。
n = torch.ones((4, 9))
n, torch.norm(n)
# (tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1.]]),
# tensor(6.))